An air bubble in a glass sphere (μ=1.5) is situated at a distance 3cm from a convex surface of diameter 10cm. At what distance from the surface will the bubble appear ?
2.5cm
−2.5cm
5cm
−5cm
The correct Answer is:B
To solve the problem of determining the apparent distance of an air bubble in a glass sphere from a convex surface, we will use the formula for refraction through a curved surface. Here’s a step-by-step solution:
Step 1: Identify the given values
- The distance of the air bubble from the convex surface (object distance, U) = 3 cm (since the bubble is inside the glass, this value is taken as negative in the formula).
- The diameter of the convex surface = 10 cm, thus the radius of curvature (R) = 10 cm / 2 = 5 cm. Since it is a convex surface, R is taken as positive, so R = +5 cm.
- The refractive index of air (n2) = 1 (since the observer is in air).
- The refractive index of glass (n1) = 1.5.
Step 2: Write the refraction formula
The formula for refraction at a curved surface is given by:
n2V−n1U=n2−n1R
Where:
- V = image distance
- U = object distance (which we will take as negative since the object is inside the medium)
- R = radius of curvature
Step 3: Substitute the values into the formula
Substituting the known values into the formula:
1V−1.5−3=1−1.55
Step 4: Simplify the equation
This simplifies to:
1V+0.5=−0.1
Step 5: Isolate 1V
Rearranging gives:
1V=−0.1−0.5
1V=−0.6
Step 6: Solve for V
Taking the reciprocal gives:
V=−10.6=−53≈−1.67 cm
Step 7: Interpret the result
The negative sign indicates that the image of the bubble appears on the same side as the object, which means it appears to be 1.67 cm in front of the convex surface.
Final Answer
The bubble will appear to be at a distance of approximately 1.67 cm from the convex surface.
---
- The distance of the air bubble from the convex surface (object distance, U) = 3 cm (since the bubble is inside the glass, this value is taken as negative in the formula).
- The diameter of the convex surface = 10 cm, thus the radius of curvature (R) = 10 cm / 2 = 5 cm. Since it is a convex surface, R is taken as positive, so R = +5 cm.
- The refractive index of air (n2) = 1 (since the observer is in air).
- The refractive index of glass (n1) = 1.5.
The formula for refraction at a curved surface is given by:
n2V−n1U=n2−n1R
Where:
- V = image distance
- U = object distance (which we will take as negative since the object is inside the medium)
- R = radius of curvature
Substituting the known values into the formula:
1V−1.5−3=1−1.55
This simplifies to:
1V+0.5=−0.1
Rearranging gives:
1V=−0.1−0.5
1V=−0.6
Taking the reciprocal gives:
V=−10.6=−53≈−1.67 cm
The negative sign indicates that the image of the bubble appears on the same side as the object, which means it appears to be 1.67 cm in front of the convex surface.
The bubble will appear to be at a distance of approximately 1.67 cm from the convex surface.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Reflection Of Light By Spherical Mirrors
Explore 5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Refraction
Explore 10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSERTION AND REASON
Explore 15 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 3
Explore 50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Book:NCERT FINGERTPS ENGLISHChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A small air bubble is situated at a distance of 3 cm from the center of a glass sphere of radius 9 cm. When viewed from the nearest side, the bubble appears to be at a distance of 5 cm from the surface. Its apparent distance when viewed from the farthest side is n×5 cm where n is?
View SolutionAn air bubble is seen inside a solid sphere of glass (n=1.5) of 4.0cm diameter at a distance of 1.0cm from the surface of the sphere (on seeing along the diameter). Determine the real position of the bubble inside the sphere.
View Solution
Knowledge Check
Light from a point source in air falls on a spherical glass surface. If μ=1.5, and radius of curvature =20cm, the distance of light source from the glass surface is 100cm , at what position will the image be formed ? (NCERT Solved Example)
A25cmB50cmC100cmD200cm
A plano-convex lens P and a concavo-convex lens Q are in contact as shown in figure. The refractive index o fthe material of the lens P and Q is 1.8and1.2 respectively. The radius of curvature of the concave surface of the lens Q is double the radius of curvature of the convex surface. The convex surface of Q is silvered.

An object is placed on the placed on the principal axis at a distance 10cm form the plane surface. The image is formed at a distance 40cm from the plane surfaces on the same side. The focal length of the system is
View SolutionA glass sphere of radius 5 cm has a small bubble at a distance 2 cm from its centre.The bubble is viewed along a Diameter of the sphere from the side on which it lies.How far from the surface will it appear.Refractive index of glass is 1.5
2.5 cm behind the surface
View SolutionThere is a small air bubble inside a glass sphere (μ=1.5) of radius 10 cm. The bubble is 4.0cm below the surface and is viewd normally from the outside. Find the apparent dipth of the bubble.
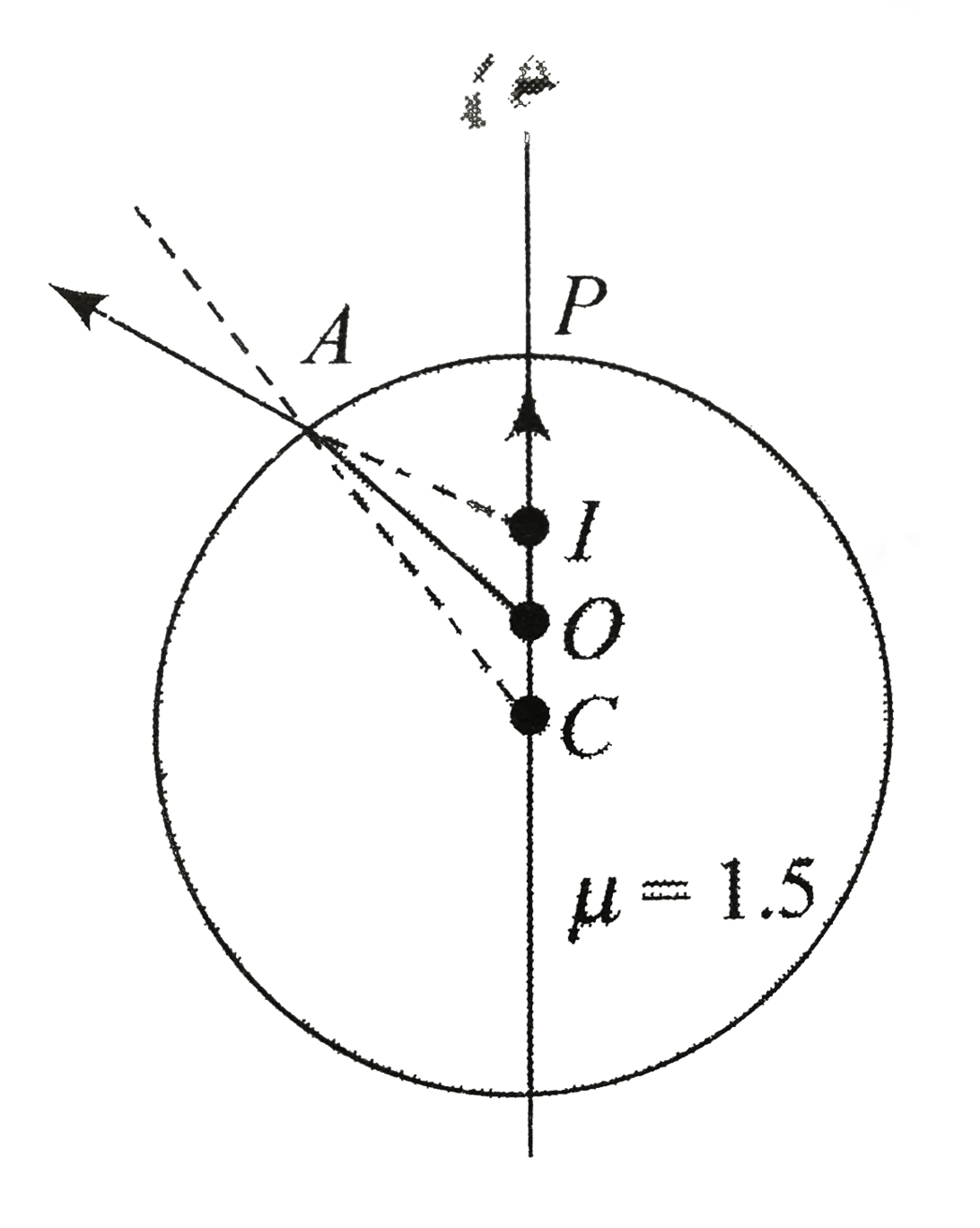
View SolutionA small air bubble in a sphere of glass with radius 4 cm appears to be 1 cm from the surface when observed along a diameter. Find the true positino of the air bubble.
View SolutionThere is small air bubble inside a glass sphere (μ=1.5) of radius 5cm. The bubble is at 'O' at 7.5cm below the surface of the glass. The sphere is placed inside water (μ=43) such that the top surface of glass is 10cm below the surface of water. The bubble is viewed normally from air. Find the apperent depth of the bubble.

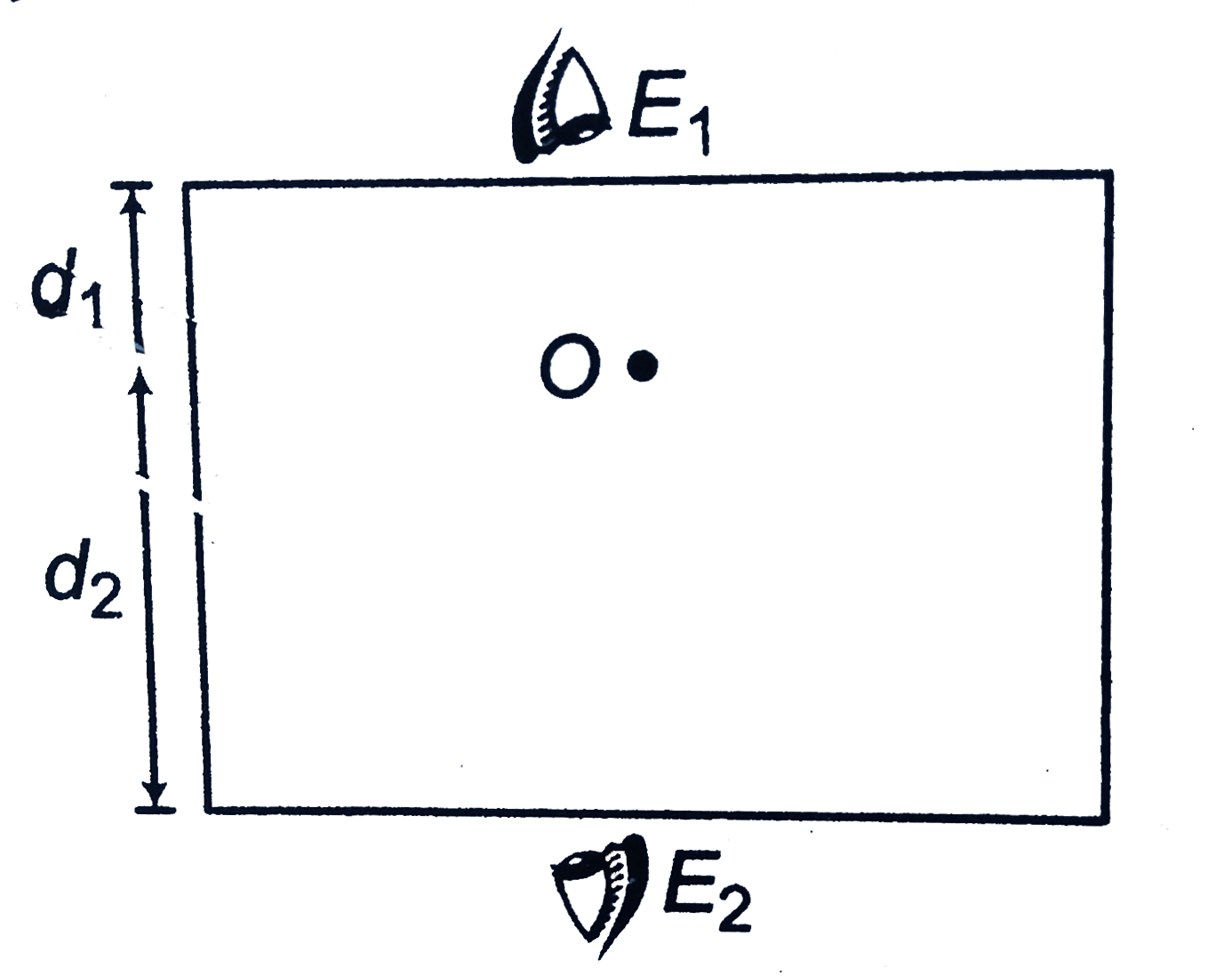
View SolutionRefractive index of the glass slab is 1.5. There is a point object O inside the slab as shown. To eyeE1 object appears at a distance of 6cm (From the top surface) and to eye E2 it appears at a distance of 8cm (from the bottom surface). Find thickness of the glass slab.
View SolutionLight from a point source in air falls on a spherical glass surface. If μ=1.5, and radius of curvature =20cm, the distance of light source from the glass surface is 100cm , at what position will the image be formed ? (NCERT Solved Example)
View Solution

