The radii of curvature of the surfaces of a double convex lens are 20cmand40cm respectively, and its focal length is 20cm. What is the refractive index of the material of the lens ?
52
43
53
45
The correct Answer is:C
To find the refractive index of the material of the lens, we can use the lens maker's formula, which is given by:
1f=(μ−1)(1R1−1R2)
Where:
- f is the focal length of the lens,
- μ is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
Step 1: Identify the given values
- R1=20cm
- R2=−40cm (the radius of curvature for the second surface is taken as negative for a convex lens)
- f=20cm
Step 2: Substitute the values into the lens maker's formula
We substitute the values into the lens maker's formula:
120=(μ−1)(120−1−40)
Step 3: Simplify the right side
Calculate 120−1−40:
120−(−140)=120+140
To add these fractions, find a common denominator:
120=240
Thus,
120+140=240+140=340
Step 4: Substitute back into the equation
Now substitute this back into the equation:
120=(μ−1)(340)
Step 5: Solve for μ−1
Rearranging gives:
μ−1=1/203/40
This can be simplified as follows:
μ−1=120⋅403=4060=23
Step 6: Solve for μ
Now, add 1 to both sides:
μ=1+23=33+23=53
Final Answer
Thus, the refractive index of the material of the lens is:
μ=53
- f is the focal length of the lens,
- μ is the refractive index of the lens material,
- R1 is the radius of curvature of the first surface,
- R2 is the radius of curvature of the second surface.
- R1=20cm
- R2=−40cm (the radius of curvature for the second surface is taken as negative for a convex lens)
- f=20cm
We substitute the values into the lens maker's formula:
Calculate 120−1−40:
Now substitute this back into the equation:
Rearranging gives:
Now, add 1 to both sides:
Thus, the refractive index of the material of the lens is:
Topper's Solved these Questions
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Reflection Of Light By Spherical Mirrors5videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - Refraction10videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTSEXERCISE - ASSERTION AND REASON15videos
RAY OPTICS AND OPTICAL INSTRUMENTS
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - PRACTICE PAPPEREXERCISE - Practice Paper 350videos
PRACTICE PAPPER
- BOOK - NCERT FINGERTPS ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS EXERCISE - Assertion And Reason15videos
SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS
Similar Questions
The radius of curvature of the faces of a double convex lens are 10cmand15cm. If focal length of lens of lens is 12cm, find the refractive index of the material of the lens.
View Solution(i) If f=+0.5m, what is the power of the lens ?
(ii) The radii of curvature of the faces of a double convex lens are 9cmand15cm. Its focal length is 12cm. What is the refractive index of glass ?
(iii) A convex lens has 20cm focal length in air. What is the focal length in water ? (Refractive index of air-water =1.33, refractive index of air-glass =1.5).View Solution
Knowledge Check
- Question 1 - Select One
The power of a biconvex lens is 10 dioptre and the radius of curvature of each surface is 10 cm. Then the refractive index of the material of the lens is
A32B43C98D53
For a plano convex lens, the radius of curvature of convex surface is 10 cm and the focal length is 30 cm. The refractive index of the material of the lens is
View SolutionThe radii of curvatures of a convex lens are 0.04 m and 0.04m. Its refractive index is 1.5. Its focal length is
View SolutionIf in a planoconvex lens, the radius of curvature of the convex surface is 10cm and the focal length is 30cm, the refractive index of the material of the lens will be
View SolutionFind the radius of curvature of the convex surface of a plan-convex lens, whose focal length is 0.3 m and the refractive index of the material of the lens is 1.5.
View SolutionThe radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
View SolutionThe radii of curvature of two spherical surfaces of a concave convex lens (μ=1.5) are 20 cm and 40 cm. (i) What is its focal length when it is in air? Also find its focal length when it is immersed in a liquid of refractive index (ii) μ=1.2 (iii) μ=2
View SolutionThe effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
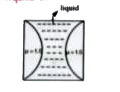 View Solution
View Solution
