The power of a biconvex lens is 10 dioptre and the radius of curvature of each surface is 10 cm. Then the refractive index of the material of the lens is
32
43
98
53
The correct Answer is:A
To find the refractive index of the material of a biconvex lens given its power and radius of curvature, we can follow these steps:
Step 1: Understand the given data
- Power of the lens, P=10 diopters
- Radius of curvature of each surface, R1=+10 cm and R2=−10 cm (since one surface is convex and the other is concave).
Step 2: Convert the power to focal length
The relationship between power P and focal length F is given by:
P=1F
Thus, we can find the focal length:
F=1P=110=0.1 m=10 cm
Step 3: Use the Lens Maker's Formula
The Lens Maker's Formula is given by:
1F=(n−1)(1R1−1R2)
Substituting the values we have:
110=(n−1)(110−1−10)
Step 4: Simplify the equation
Calculate the right-hand side:
110−1−10=110+110=210=15
Now substituting this back into the equation:
110=(n−1)(15)
Step 5: Solve for n
Rearranging gives:
n−1=110⋅5=12
Thus:
n=12+1=32
Conclusion
The refractive index of the material of the lens is:
n=32
- Power of the lens, P=10 diopters
- Radius of curvature of each surface, R1=+10 cm and R2=−10 cm (since one surface is convex and the other is concave).
The relationship between power P and focal length F is given by:
P=1F
Thus, we can find the focal length:
F=1P=110=0.1 m=10 cm
The Lens Maker's Formula is given by:
1F=(n−1)(1R1−1R2)
Substituting the values we have:
110=(n−1)(110−1−10)
Calculate the right-hand side:
110−1−10=110+110=210=15
Now substituting this back into the equation:
110=(n−1)(15)
Rearranging gives:
n−1=110⋅5=12
Thus:
n=12+1=32
The refractive index of the material of the lens is:
n=32
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Reflection Of Light By Spherical Mirrors
Explore 5 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:Refraction
Explore 10 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTSBook:NCERT FINGERTPS ENGLISHChapter:RAY OPTICS AND OPTICAL INSTRUMENTSExercise:ASSERTION AND REASON
Explore 15 Videos
- PRACTICE PAPPERBook:NCERT FINGERTPS ENGLISHChapter:PRACTICE PAPPERExercise:Practice Paper 3
Explore 50 Videos
- SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Book:NCERT FINGERTPS ENGLISHChapter:SEMICONDUCTOR ELECTRONICS : MATERIALS , DEVICES AND SIMPLE CIRCUITS Exercise:Assertion And Reason
Explore 15 Videos
Similar Questions
A plano-convex lens is silvered on its plane side. The radius of curvature of the other face is 12cm and the refractive index of the material of the lens is 1.5. An object is placed 24 cm in front of the silvered lens. Where will the image be formed?
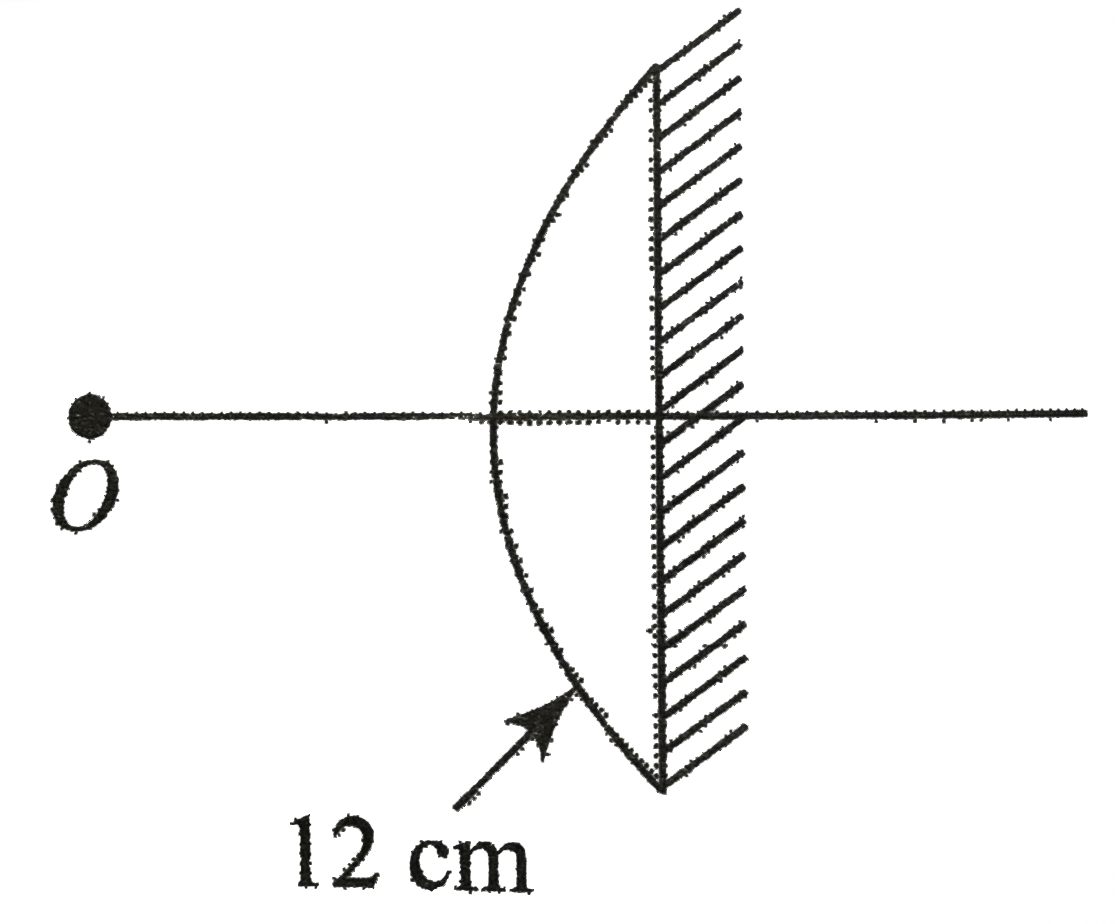
View SolutionFor a plano convex lens, the radius of curvature of convex surface is 10 cm and the focal length is 30 cm. The refractive index of the material of the lens is
View Solution
Knowledge Check
A biconvex lens has focal length 23 times the radius of curvature of either surface. Calculate refraction index f material of the lens.
A1.75B1.33C1.5D1.0The radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.
If in a planoconvex lens, the radius of curvature of the convex surface is 10cm and the focal length is 30cm, the refractive index of the material of the lens will be
View SolutionThe focal length of an equi-concave lens is 34 times of radius of curvature of its surfaces. Find the refractive index of the material of lens. Under what condition will this lens behave as a converging lens?
View SolutionA converging bundle of rays is intercepted by a biconcave lens. The radii of curvature of both surfaces are 20cm and the refractive index of the material of the lens is 1.5. If the rays originially converged to a point 10cm in front of the lens, where will they now converge after passing through the lens?

View SolutionA biconvex lens has focal length 23 times the radius of curvature of either surface. Calculate refraction index f material of the lens.
View SolutionConsider an equiconvex lens of radius of curvature R and focal length f. If f>R , the refractive index μ of the material of the lens
View SolutionThe radius of curvature of the faces of a double convex lens are 10cmand15cm. If focal length of lens of lens is 12cm, find the refractive index of the material of the lens.
View Solution

