Question

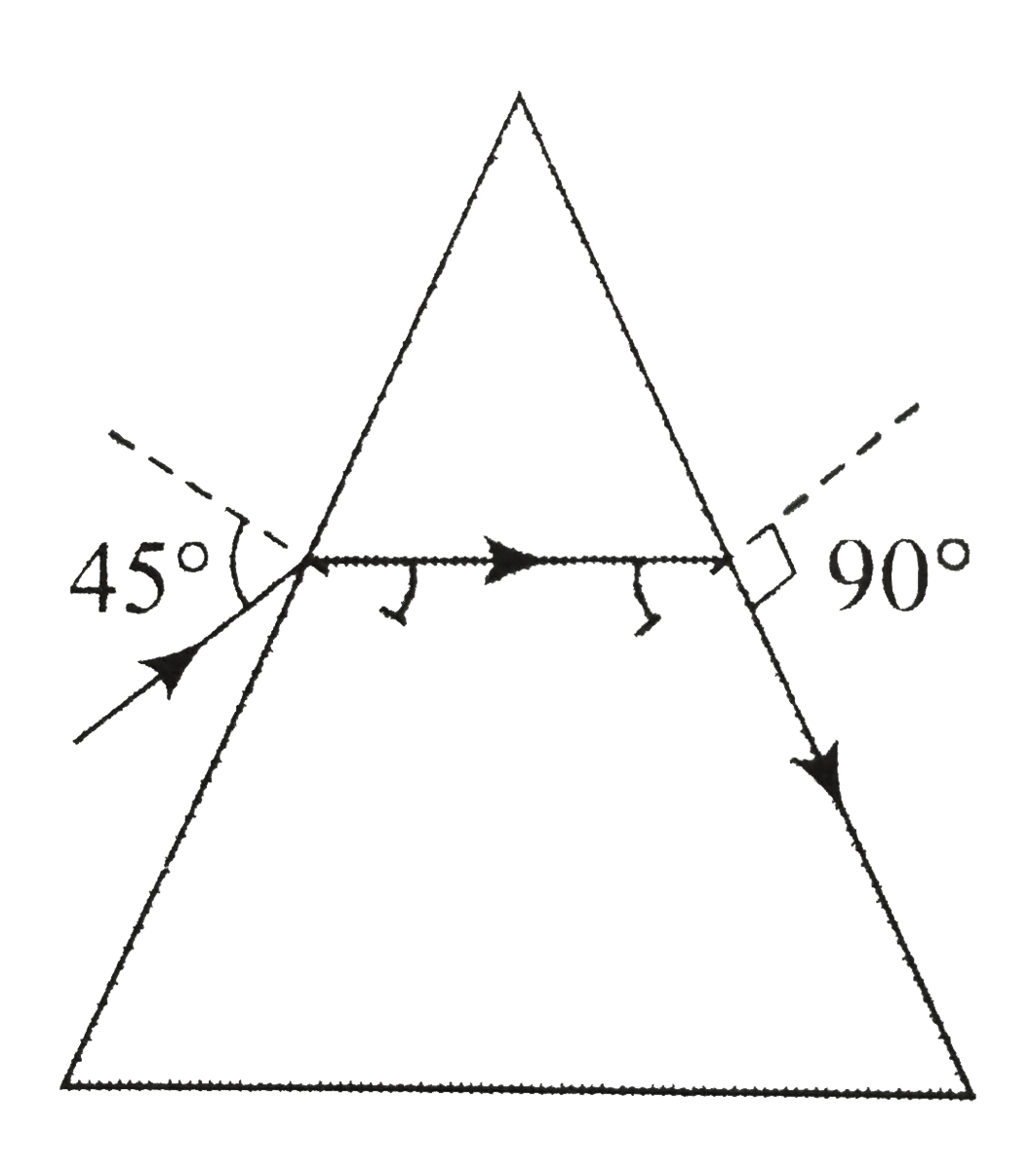
A ray of light is incident at small angle I on the surface of prism of small angle A and emerges normally from the oppsite surface. If the refractive index of the material of the prism is mu, the angle of incidence is nearly equal to

Options

A. `A/mu`
B. `A/(2mu)`
C. `muA`
D. `(muA)/(2)`

Answer

C

Explanation

To solve the problem step by step, we will analyze the situation involving the prism and the light ray.

Step 1: Understand the Given Information
- A ray of light is incident at a small angle \( I \) on the surface of a prism with a small angle \( A \).
- The ray emerges normally from the opposite surface of the prism.
- The refractive index of the material of the prism is \( \mu \).

Step 2: Identify the Angles
- Let \( i \) be the angle of incidence.
- The angle of emergence \( e \) is given as \( 0 \) degrees since the ray emerges normally.

Step 3: Use the Relation for Small Angles
For a small angle prism, the angle of deviation \( \delta \) can be approximated using the formula:
\( \delta = (\mu - 1) A \)
where \( A \) is the angle of the prism.

Step 4: Relate the Angles
Using the relationship between the angles, we have:
\( i + e = A + \delta \)
Substituting \( e = 0 \):
\( i = A + \delta \)

Step 5: Substitute the Deviation
Now substitute the expression for \( \delta \):
\( i = A + (\mu - 1) A \)
This simplifies to:
\( i = A + \mu A - A \)
\( i = \mu A \)

Step 6: Final Expression
Thus, the angle of incidence \( i \) is given by:
\( i = \mu A \)

Conclusion
The angle of incidence \( i \) is nearly equal to \( \mu A \).