Two thermally insulated vessel 1 and 2 are filled with air at temperature (T1T2),volume(V1V2) and pressure (P1P2) respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
T1+T2
(T1+T2)2
T1T2(P1V1+P2V2)P1V1T2+P2V2T1
T1T2(P1V1+P2V2)
The correct Answer is:C
To find the equilibrium temperature T when two thermally insulated vessels are connected, we can follow these steps:
1. Understanding the System:
- We have two thermally insulated vessels (1 and 2) filled with air at temperatures T1 and T2, volumes V1 and V2, and pressures P1 and P2 respectively.
2. Applying the First Law of Thermodynamics:
- Since the vessels are thermally insulated, there is no heat exchange (ΔQ=0) and no work done (ΔW=0). Therefore, the change in internal energy (ΔU) is also zero.
- This implies that the total internal energy before opening the valve is equal to the total internal energy after opening the valve:
U1+U2=U
3. Internal Energy of Ideal Gases:
- For an ideal gas, the internal energy U can be expressed as:
U=nCvT
- Where n is the number of moles, Cv is the specific heat at constant volume, and T is the temperature.
4. Calculating Moles:
- The number of moles in each vessel can be calculated using the ideal gas law:
n1=P1V1RT1andn2=P2V2RT2
5. Setting Up the Equation:
- The total internal energy before the valve is opened can be written as:
U1+U2=n1CvT1+n2CvT2
- After opening the valve, the internal energy can be expressed as:
U=(n1+n2)CvT
- Setting these equal gives:
n1CvT1+n2CvT2=(n1+n2)CvT
6. Cancelling Cv:
- Since Cv is a common factor, we can cancel it from both sides:
n1T1+n2T2=(n1+n2)T
7. Solving for T:
- Rearranging gives:
T=n1T1+n2T2n1+n2
8. Substituting for n1 and n2:
- Substitute n1 and n2:
T=(P1V1RT1)T1+(P2V2RT2)T2P1V1RT1+P2V2RT2
- Simplifying gives:
T=P1V1+P2V2P1V1T1+P2V2T2
9. Final Expression:
- Thus, the equilibrium temperature T is given by:
T=P1V1T2+P2V2T1P1V1+P2V2
- We have two thermally insulated vessels (1 and 2) filled with air at temperatures T1 and T2, volumes V1 and V2, and pressures P1 and P2 respectively.
- Since the vessels are thermally insulated, there is no heat exchange (ΔQ=0) and no work done (ΔW=0). Therefore, the change in internal energy (ΔU) is also zero.
- This implies that the total internal energy before opening the valve is equal to the total internal energy after opening the valve:
U1+U2=U
- For an ideal gas, the internal energy U can be expressed as:
U=nCvT
- Where n is the number of moles, Cv is the specific heat at constant volume, and T is the temperature.
- The number of moles in each vessel can be calculated using the ideal gas law:
n1=P1V1RT1andn2=P2V2RT2
- The total internal energy before the valve is opened can be written as:
U1+U2=n1CvT1+n2CvT2
- After opening the valve, the internal energy can be expressed as:
U=(n1+n2)CvT
- Setting these equal gives:
n1CvT1+n2CvT2=(n1+n2)CvT
- Since Cv is a common factor, we can cancel it from both sides:
n1T1+n2T2=(n1+n2)T
- Rearranging gives:
T=n1T1+n2T2n1+n2
- Substitute n1 and n2:
T=(P1V1RT1)T1+(P2V2RT2)T2P1V1RT1+P2V2RT2
- Simplifying gives:
T=P1V1+P2V2P1V1T1+P2V2T2
- Thus, the equilibrium temperature T is given by:
T=P1V1T2+P2V2T1P1V1+P2V2
Topper's Solved these Questions
Similar Questions
Two containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo containers of equal volume contain the same gas at pressure P1 and P2 and absolute temperature T1 and T2, respectively. On joining the vessels, the gas reaches a common pressure P and common temperature T. The ratio P/T is equal to
View SolutionTwo chemically non-reactive gases are separately contained in two vessels of same capacity at pressure P1, and P2, respectively. If two vessels are connected, the total pressure of gaseous mixture will be
View SolutionTwo chemically non-reactive gases are separately contained in two vessels of same capacity at pressure P1 and P2 respectively. If two vessels are connected, the total pressure of gaseous mixture will
View SolutionA thermally insulated vessels contains two liquids with initial temperature T1 and T2 and specific heats C0 and 2C0, separted by a non conducting partition. The partition is removed, and the difference between the initial temperature of one of the liquids and the temperature T established in the vessel turns out to be equal to half the difference between the initial temperatures of the liquids. Determine the ratio of M1/M2 of the masses of the liquids.

View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View SolutionThe velocities of sound in an ideal gas at temperature T1andT2 K are found to be V1andV2 respectively. If ther.m.s velocities of the molecules of the same gas at the same temperatures T1andT2 are v1andv2 respectively then
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
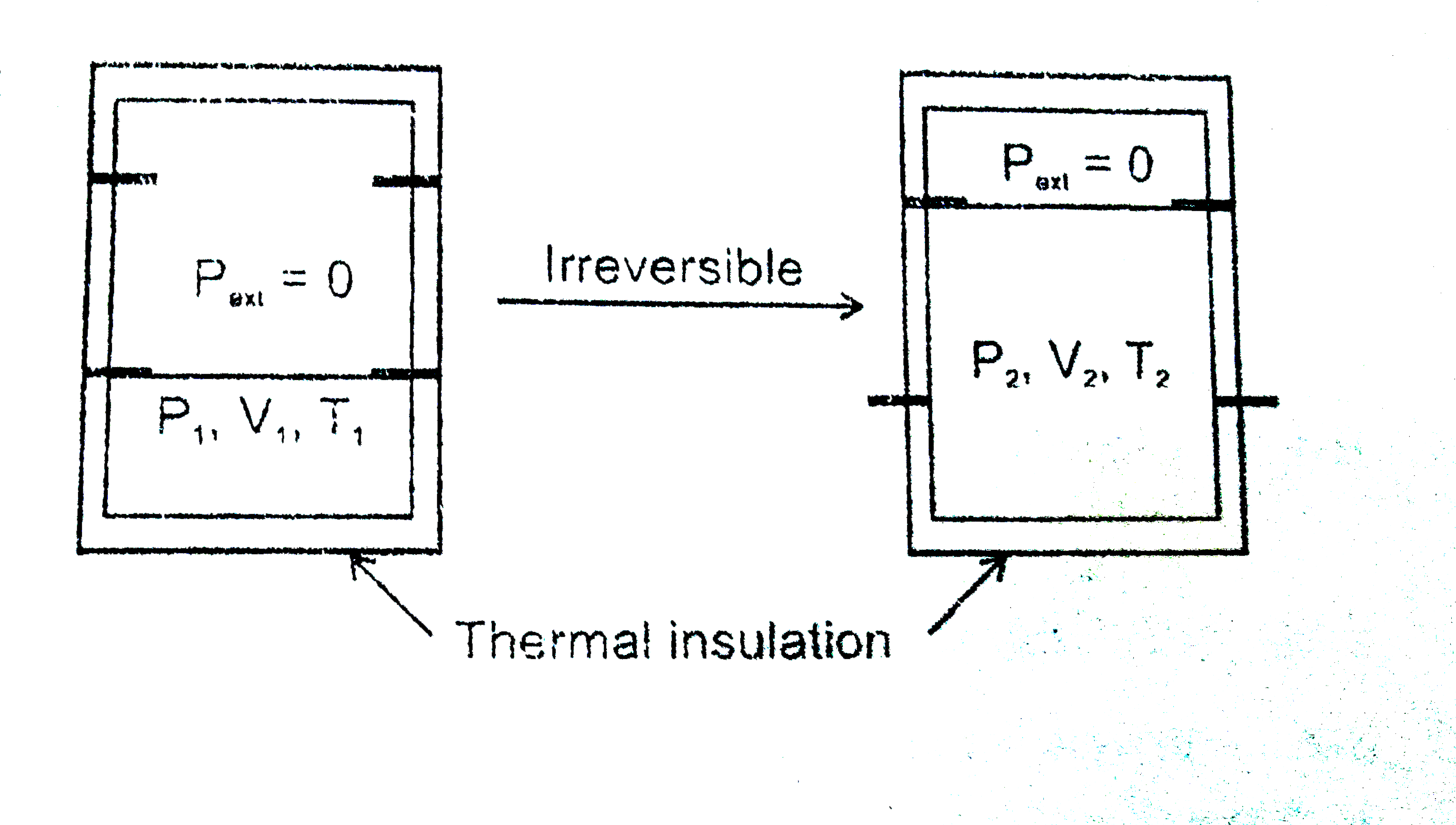
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure =P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2 and T2 respectively. For this expansion.
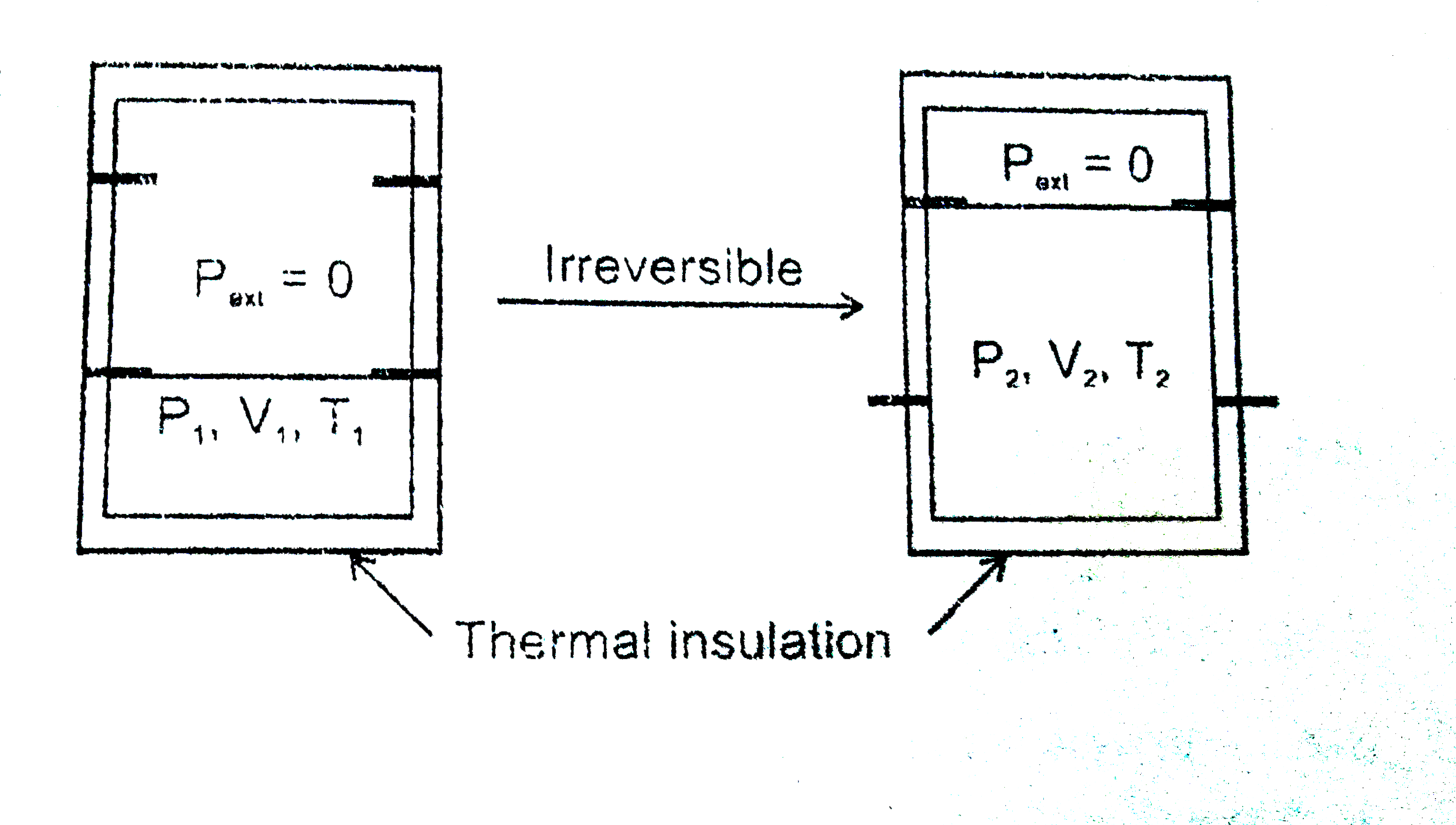
View SolutionAn ideal gas in a thermally insulated vessel at internal pressure = P1, volume =V1 and absolute temperature =T1 expands irreversibly against zero external pressure, as shown in the diagram. The final internal pressure, volume and absolute temperature of the gas are P2,V2andT2, respectively. For this expansion.
View Solution

