A liquid of density ρ flows along a horizontal pipe of uniform cross-section A with a velocity v through a right angled bend as shown in fig. What force has to be exerted at the bend to hold the pipe in equilibrium ? .
2aρv2
aρv2/√2
√2aρv2
aρv2
The correct Answer is:C
To find the force that must be exerted at the bend of a horizontal pipe to hold it in equilibrium, we can follow these steps:
1. Understand the Situation:
- We have a liquid flowing through a horizontal pipe with a uniform cross-section and a right-angled bend. The liquid has a density ρ and flows with a velocity v.
2. Identify the Change in Momentum:
- As the liquid flows through the bend, it changes direction. The change in momentum is crucial to determine the force required to keep the pipe in equilibrium.
3. Calculate the Mass Flow Rate:
- The mass flow rate dmdt can be calculated using the formula:
dmdt=ρAv
- Here, A is the cross-sectional area of the pipe, and v is the velocity of the liquid.
4. Determine the Force:
- The force exerted by the liquid due to the change in momentum can be expressed as:
F=dmdt⋅v
- Substituting the mass flow rate into this equation gives:
F=(ρAv)⋅v=ρAv2
5. Consider the Resultant Force at the Bend:
- At the bend, the forces acting on the pipe can be resolved into two components (one vertical and one horizontal). The resultant force R at the bend can be calculated as:
R=√F2+F2=√2F2=√2F
- Since both components are equal, we can express this as:
R=√2⋅(ρAv2)
6. Final Expression for the Force:
- Therefore, the total force that must be exerted at the bend to hold the pipe in equilibrium is:
F=ρAv2
Conclusion:
The force that has to be exerted at the bend to hold the pipe in equilibrium is F=ρAv2.
- We have a liquid flowing through a horizontal pipe with a uniform cross-section and a right-angled bend. The liquid has a density ρ and flows with a velocity v.
- As the liquid flows through the bend, it changes direction. The change in momentum is crucial to determine the force required to keep the pipe in equilibrium.
- The mass flow rate dmdt can be calculated using the formula:
dmdt=ρAv
- Here, A is the cross-sectional area of the pipe, and v is the velocity of the liquid.
- The force exerted by the liquid due to the change in momentum can be expressed as:
F=dmdt⋅v
- Substituting the mass flow rate into this equation gives:
F=(ρAv)⋅v=ρAv2
- At the bend, the forces acting on the pipe can be resolved into two components (one vertical and one horizontal). The resultant force R at the bend can be calculated as:
R=√F2+F2=√2F2=√2F
- Since both components are equal, we can express this as:
R=√2⋅(ρAv2)
- Therefore, the total force that must be exerted at the bend to hold the pipe in equilibrium is:
F=ρAv2
The force that has to be exerted at the bend to hold the pipe in equilibrium is F=ρAv2.
Topper's Solved these Questions
Similar Questions
A liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
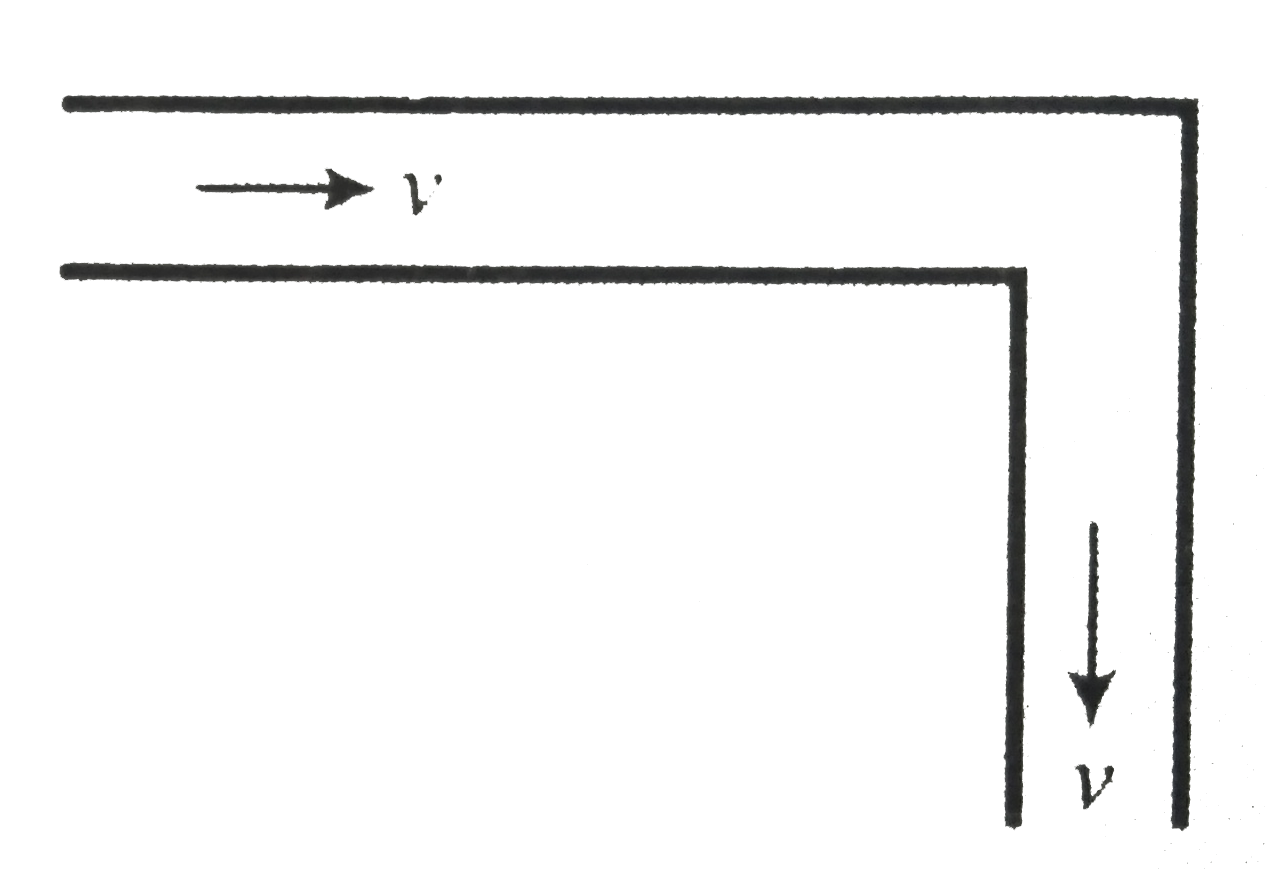
View SolutionA liquid is flowing in a horizontal pipe of non-uniform cross section. Which of the following quantities may remain unchanged with respect to time?
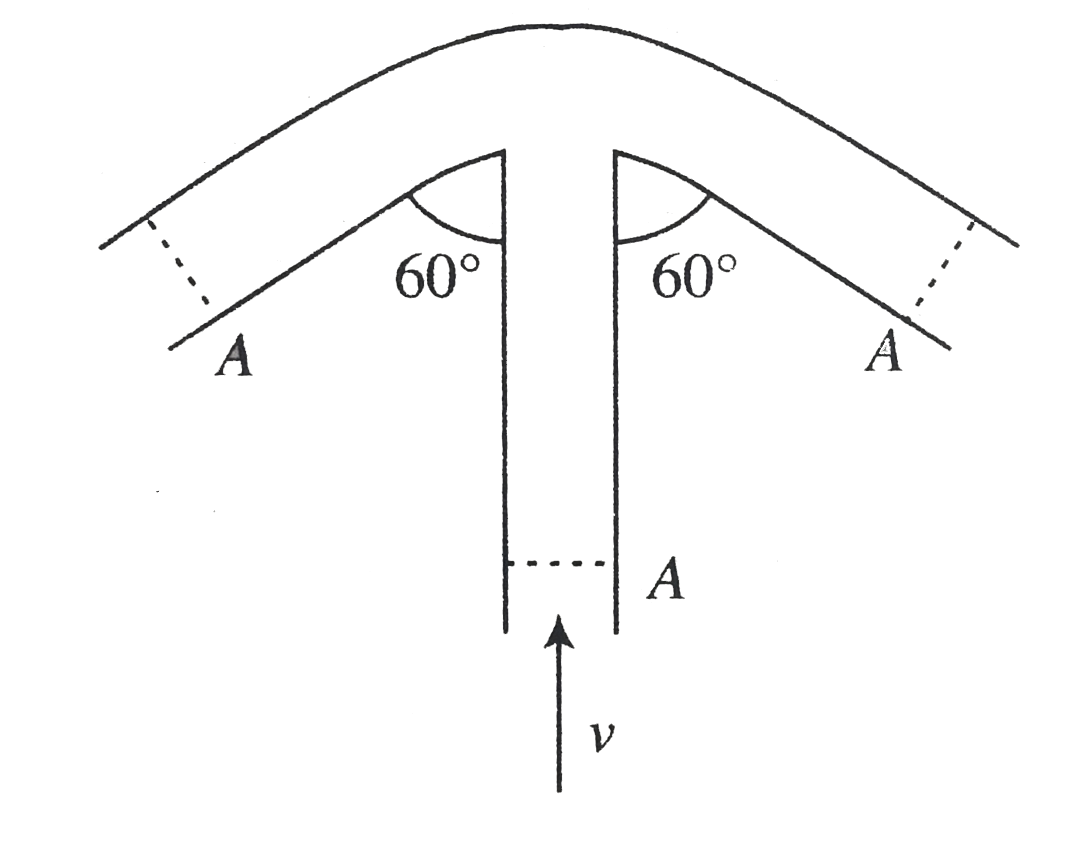
View SolutionAn ideal liquid of density ρ is pushed with velocity v through the central limb of the tube shown in fig. What force does the liquid exert on the tube? The cross sectional areas of the three limbs are equal to A each. Assume stream-line flow.
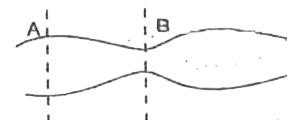
View SolutionA horizontal pipe of shown cross - section has a liquid flowing through it and follows Bernouli's theorem . Which of the following is/are constant through out pipe ?
View Solution_S01_083_Q01.png)
Water (density ρ) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)
View SolutionA liquid is flowing through a pipe of non-uniform cross-section. At a point where area of cross-section of the pipe is less, match the following columns.

View SolutionAn incompressible liquid is flowing through a horizontal pipe as shown in figure. Find the value of v.
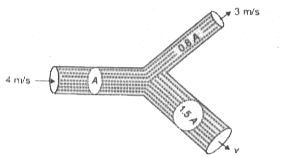
View SolutionAn incompressible liquid is flowing through a horizontal pipe as shown in figure. The value of speed v is
View SolutionAn ideal fluid flows through a pipe of circular cross - section with diameters 5 cm and 10 cm as shown in the figure. The ratio of velocities of fluid at A and B is

View SolutionWater is flowing through a horizontal tube of non-uniform cross-section. At a place, the radius of the tube is 1.0cm and the velocity of water is 2m/s. What will be the velocity of water where the radius of the pipe is 2.0cm?
View Solution

