An ideal liquid of density ρ is pushed with velocity v through the central limb of the tube shown in fig. What force does the liquid exert on the tube? The cross sectional areas of the three limbs are equal to A each. Assume stream-line flow.

98ρAv2
54ρAv2
32ρAv2
ρAv2
The correct Answer is:B
Velocity of liquid through inclined limbs = v2
Rate of change of momentum of the liquid is
=ρAv2+2[ρA(v2)2cos60∘]=54ρAv2.
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Multiple Correct
11 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Assertion-reasoning
15 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Subjective
15 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Integer type
1 Videos
Similar Questions
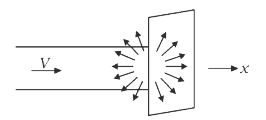
A liquid of density ρ is flowing with a speed V through a pipe of cross sectional area A. What force does the liquid stream exert on wall in x direction if it splashes in the form of a circle after it hits the wall?
View SolutionIf cross- sectional area of limb I is A1 and that of limb II is A2 then velocity of the liquid in the tube will be, (cross- sectional area of tube is very small)

View Solution
Knowledge Check
A liquid of density ρ flows along a horizontal pipe of uniform cross-section A with a velocity v through a right angled bend as shown in fig. What force has to be exerted at the bend to hold the pipe in equilibrium ? .
A2aρv2Baρv2/√2C√2aρv2Daρv2
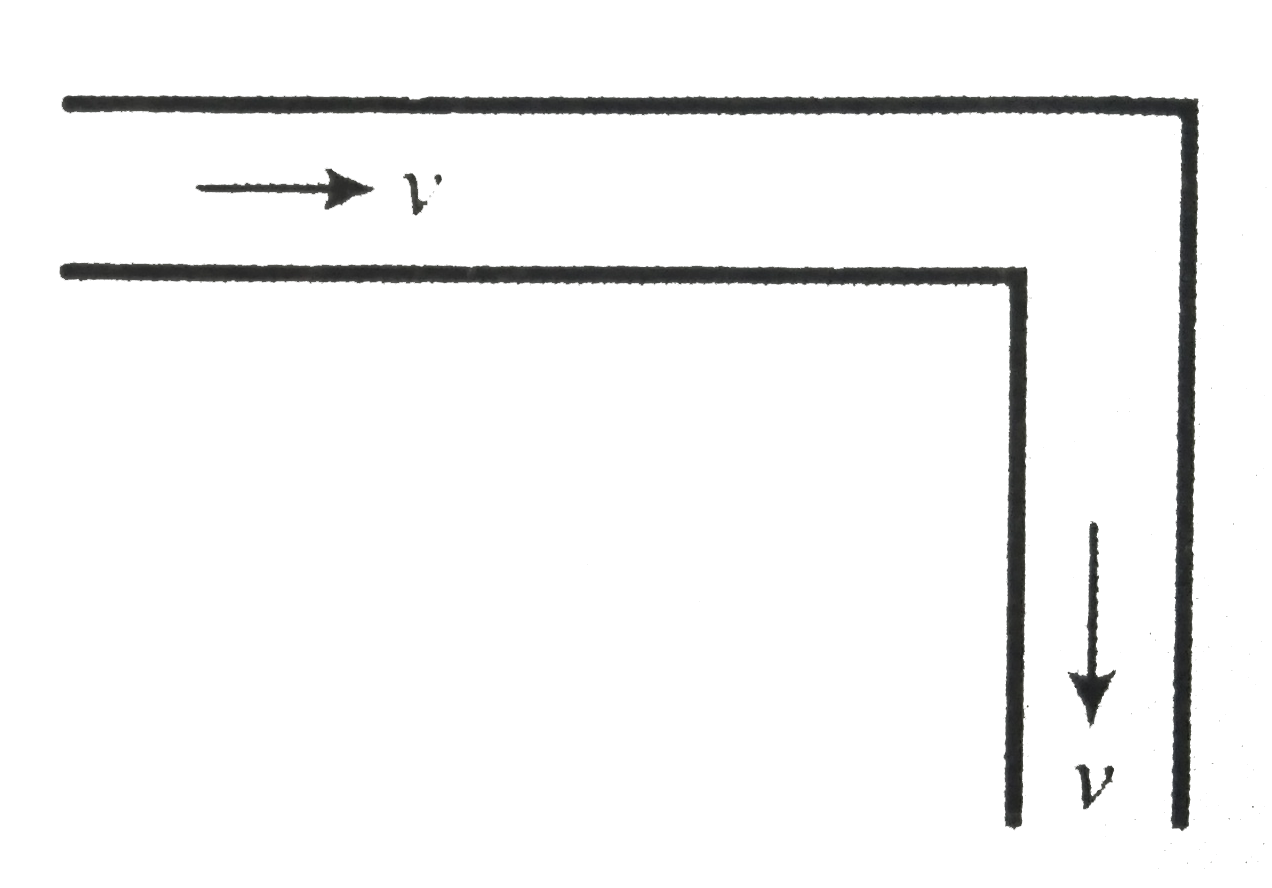
A liquid of density ρ is flowing with a speed v through a pipe of cross sectional area A. The pipe is bent in the shape of a right angles as shown. What force should be exerted on the pipe at the corner to keep it fixed?
View SolutionA non viscous liquid of density ρ is filled in a tube with A as the area of cross section, as shown in the figure. If the liquid is slightly depressed in one of the arms, the liquid column oscillates with a frequency

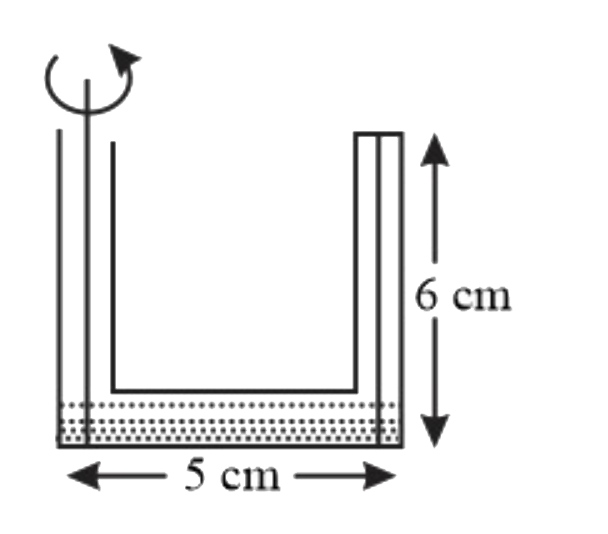
View SolutionLength of the horizontal arm of a uniform cross - section U - tube is l = 5 cm and both ends of the vertical arms are open to the surrounding pressure of 7700 N m−2. A liquid of density ρ=103 kg m−3 is poured into the tube such that the liquid just fills the horizontal part of the tube. Now, one of the open ends is sealed and the tube. Now, one of the open ends is sealed and the tube is then rotaed about a vertical axis passing through the other veritcal arm with angular velocity ω due to which the liquid rises up to half the length of the vertical arm. If length of each vertical arm is a = 6 cm. What is the value of ω(in rad s−1)?
View SolutionAn incompressible liquid flows through a horizontal tube as shown in the figure. Then the velocity 'v' of the fluid is:

View SolutionA steel bolt is insertede into a copper tube as shown in the figure. Find the forces induced in the bolt and in the tube when the nut is turned through one revolution. Assume that the length of the tube is l, the pitch of the bolt thread is h and the cross sectional areas of the steel bolt and the copper tube are As and Ac respectively.

View SolutionLength of horizontal arm of a uniform cross section U-tube is l=21cm and ends of both of the vertical arms are open to surrounding of pressure 10500N/m2. A liquid of density ρ=103kg/m3 is poured into the tube such that liquid just fills the horizontal part of the tube. Now one of the open ends is sealed and the tube is then rotated about a vertical axis passing through the other vertical arm With angular velocity ω0=10rad/s. If length of each vertical arm is a=6cm, calculate the length of air column in the sealed arm. (in cm)

View Solution_S01_083_Q01.png)
Water (density ρ) is flowing through the uniform tube of cross-sectional area A with a constant speed v as shown in the figure. Find the magnitude of force exerted by the water on the curved corner of the tube is (neglect viscous forces)
View Solution
