A weightless spring of length 60 cm and force constant 100Nm−1 is kept straight and unstretched on a smooth horizontal table and its ends are rigidly fixed. A mass of 0.25 kg is attached at the middle of the spring and is slightly displaced along the length. The time period of the oscillation of the mass is
π20 s
π10 s
π5 s
π√200 s
The correct Answer is:A
To find the time period of oscillation of a mass attached to a weightless spring that is fixed at both ends, we can follow these steps:
1. Identify the parameters:
- Length of the spring (L) = 60 cm = 0.6 m
- Spring constant (k) = 100 N/m
- Mass (m) = 0.25 kg
2. Understanding the system:
- The spring is fixed at both ends, and a mass is attached at the middle. When the mass is displaced slightly, it will oscillate due to the restoring force provided by the spring.
3. Determine the effective spring constant:
- When the spring is fixed at both ends and a mass is attached at the center, the spring can be considered as two springs in series, each with a spring constant of k.
- The effective spring constant (k_eff) for two springs in series is given by:
keff=k2
- Therefore, for our case:
keff=100N/m2=50N/m
4. Calculate the angular frequency (ω):
- The angular frequency (ω) for a mass-spring system is given by:
ω=√keffm
- Substituting the values:
ω=√50N/m0.25kg=√200s−2=10s−1
5. Calculate the time period (T):
- The time period (T) is related to the angular frequency by:
T=2πω
- Substituting the value of ω:
T=2π10=π5s
Final Answer:
The time period of the oscillation of the mass is:
T=π5s
- Length of the spring (L) = 60 cm = 0.6 m
- Spring constant (k) = 100 N/m
- Mass (m) = 0.25 kg
- The spring is fixed at both ends, and a mass is attached at the middle. When the mass is displaced slightly, it will oscillate due to the restoring force provided by the spring.
- When the spring is fixed at both ends and a mass is attached at the center, the spring can be considered as two springs in series, each with a spring constant of k.
- The effective spring constant (k_eff) for two springs in series is given by:
keff=k2
- Therefore, for our case:
keff=100N/m2=50N/m
- The angular frequency (ω) for a mass-spring system is given by:
ω=√keffm
- Substituting the values:
ω=√50N/m0.25kg=√200s−2=10s−1
- The time period (T) is related to the angular frequency by:
T=2πω
- Substituting the value of ω:
T=2π10=π5s
The time period of the oscillation of the mass is:
T=π5s
Topper's Solved these Questions
Similar Questions
A spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table as shown in figure. A mass of 3.0kg is attached to the free end of the spring, pulled side ways to a distance of 2.0cm and released. Determing.
(a) the frequency of oscillation of the mass.
(b) the maximum acceleration of the mass.
(c) the maximum speed of the mass.

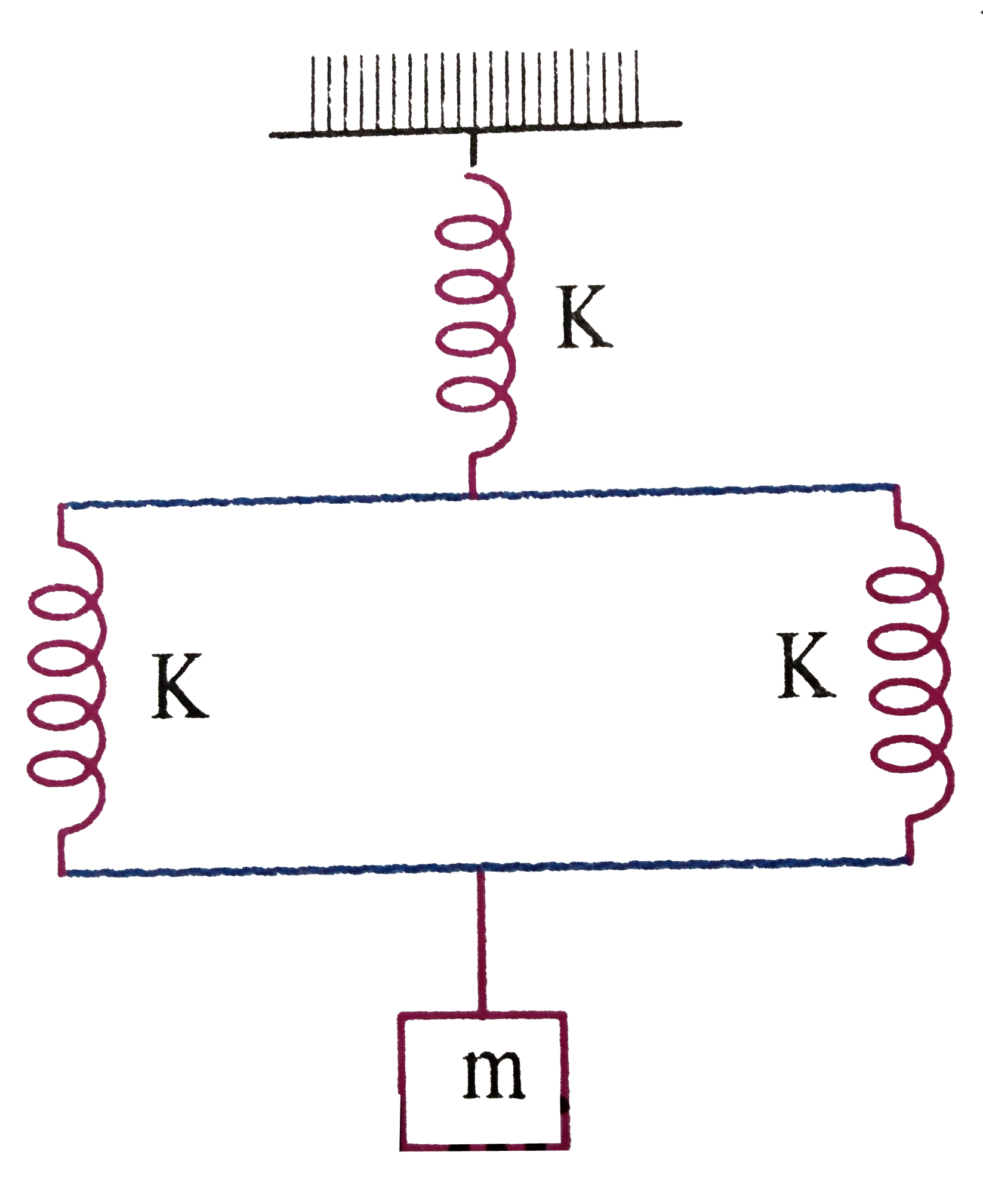
View SolutionA body of mass m is suspended from three springs as shown in figure. If mass m is displaced slightly then time period of oscillation is
View SolutionA block of mass m hangs from three springs having same spring constant k. If the mass is slightly displaced downwards, the time period of oscillation will be

View SolutionA spring of force constant 1200Nm−1 is mounted on a horizontal table and a mass of 3.0 kg of attached to the free and of the spring. The mass is made to rotate with an angular velocity of 10 rad/s. What is the elongation produced in the spring if its unstretched length is 60 cm ?
View SolutionA block of mass m lie on a horizontal smooth surface and connected with the springs at their natural length as shown in figure. When block slightly displaced then find the time period of oscillation.

View SolutionA spring of force constant 600Nm−1 is mounted on a horizontal table. A mass of 1.5 kg is attached to the free end of the spring,pulled sideways to a distance of 2 cm and released . The speed of the mass when the spring is compressed by 1 cm is
View SolutionA body of mass m is suspended from vertical spring and is set into simple harmonic oscillations of time period T. Next the spring is fixed at one end on a smooth horizontal table and same body is attached at the other end. The body is pulled slightly and then released to produce horizontal oscillations of the spring. The time period of horizontal oscillations is
View SolutionA rod of mass m and length L is kept on a horizontal smooth surface. The rod is hinged at its one end A. There are two springs, perpendicular to the rod, kept in the same horizontal plane. The spring of spring constant k is rigidly attached to the lower end of rod and spring of spring constant 12k just touches the rod at its midpoint C, as shown in the figure. If the rod is slightly displaced leftward and released then, the time period for small osciallation of the rod will be

View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View Solution

