A metal wire of length L1 and area of cross section A is ttached to a rigid support. Another metal wire of length L2 and of the same cross sectional area is attached to the free end of the first wire. A body of mass M is then suspended from the free end of the second wire, if Y1 and Y2 are the Young's moduli of the wires respectively the effective force constant of the system of two wires is
Y1Y2A2(Y1L2+Y2L1)
Y1Y2A(L1L2)1/2
Y1Y2A(Y1L2+Y2L1)
(Y1Y2)1/2A(L1L2)1/2
The correct Answer is:C
To find the effective force constant of the system of two wires, we can follow these steps:
Step 1: Understand the System
We have two metal wires of lengths L1 and L2 with the same cross-sectional area A. The Young's moduli for these wires are Y1 and Y2 respectively. A mass M is suspended from the free end of the second wire.
Step 2: Define the Force Constants
The force constant k for a wire can be derived from the Young's modulus formula:
Y=StressStrain=F/AΔL/L
Rearranging gives:
Y=FLAΔL
From this, we can express the force constant k as:
k=YAL
Step 3: Calculate Force Constants for Each Wire
For the first wire (length L1 and Young's modulus Y1):
k1=Y1AL1
For the second wire (length L2 and Young's modulus Y2):
k2=Y2AL2
Step 4: Combine the Force Constants
Since the wires are in series, the effective force constant kequiv can be calculated using the formula for series springs:
1kequiv=1k1+1k2
Substituting k1 and k2:
1kequiv=L1Y1A+L2Y2A
Step 5: Simplify the Equation
Combining the fractions:
1kequiv=L1Y2+L2Y1Y1Y2A
Taking the reciprocal gives:
kequiv=Y1Y2AL1Y2+L2Y1
Final Result
Thus, the effective force constant of the system of two wires is:
kequiv=Y1Y2AL1Y2+L2Y1
---
We have two metal wires of lengths L1 and L2 with the same cross-sectional area A. The Young's moduli for these wires are Y1 and Y2 respectively. A mass M is suspended from the free end of the second wire.
The force constant k for a wire can be derived from the Young's modulus formula:
Y=StressStrain=F/AΔL/L
Rearranging gives:
Y=FLAΔL
From this, we can express the force constant k as:
k=YAL
For the first wire (length L1 and Young's modulus Y1):
k1=Y1AL1
For the second wire (length L2 and Young's modulus Y2):
k2=Y2AL2
Since the wires are in series, the effective force constant kequiv can be calculated using the formula for series springs:
1kequiv=1k1+1k2
Substituting k1 and k2:
1kequiv=L1Y1A+L2Y2A
Combining the fractions:
1kequiv=L1Y2+L2Y1Y1Y2A
Taking the reciprocal gives:
kequiv=Y1Y2AL1Y2+L2Y1
Thus, the effective force constant of the system of two wires is:
kequiv=Y1Y2AL1Y2+L2Y1
Topper's Solved these Questions
Similar Questions
A wire of length L,area of cross section A is hanging from a fixed support. The length of the wire changes to L1 when mass M is suspended from its free end. The expression for Young's modulus is:
View SolutionOne end of a Nichrome wire of length 2L and cross-sectional area A is attached to an end of another Nichrome wire of length L and cross-sectional area 2A. If the free end of the longer wire is at an electric potential of 8.0 volts, and the free end of the shorter wire is at an electric potential 1.0 volts, the potential at the junction of the two wires is equal to
View Solution
Knowledge Check
A wire of length L and area of cross-section A, is stretched by a load. The elongation produced in the wire is I. If Y is the Young's modulus of the material of the wire, then the force constant of the wire is
AYLABYlACYALDYAlA wire of length L and cross-sectional area A is made of a material of Young's modulus Y. IF the wire is stretched by an amount x, the workdone is
AYAx22LBYAx2L2CYAx2LDYAx2L
A body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
View SolutionA mild steel wire of length 1.0m and cross sectional area 2L is strethched, within its elastic limit horizontally between two pillars(figure). A mass of m is suspended form the midpont of the wire. Strain in the wire is
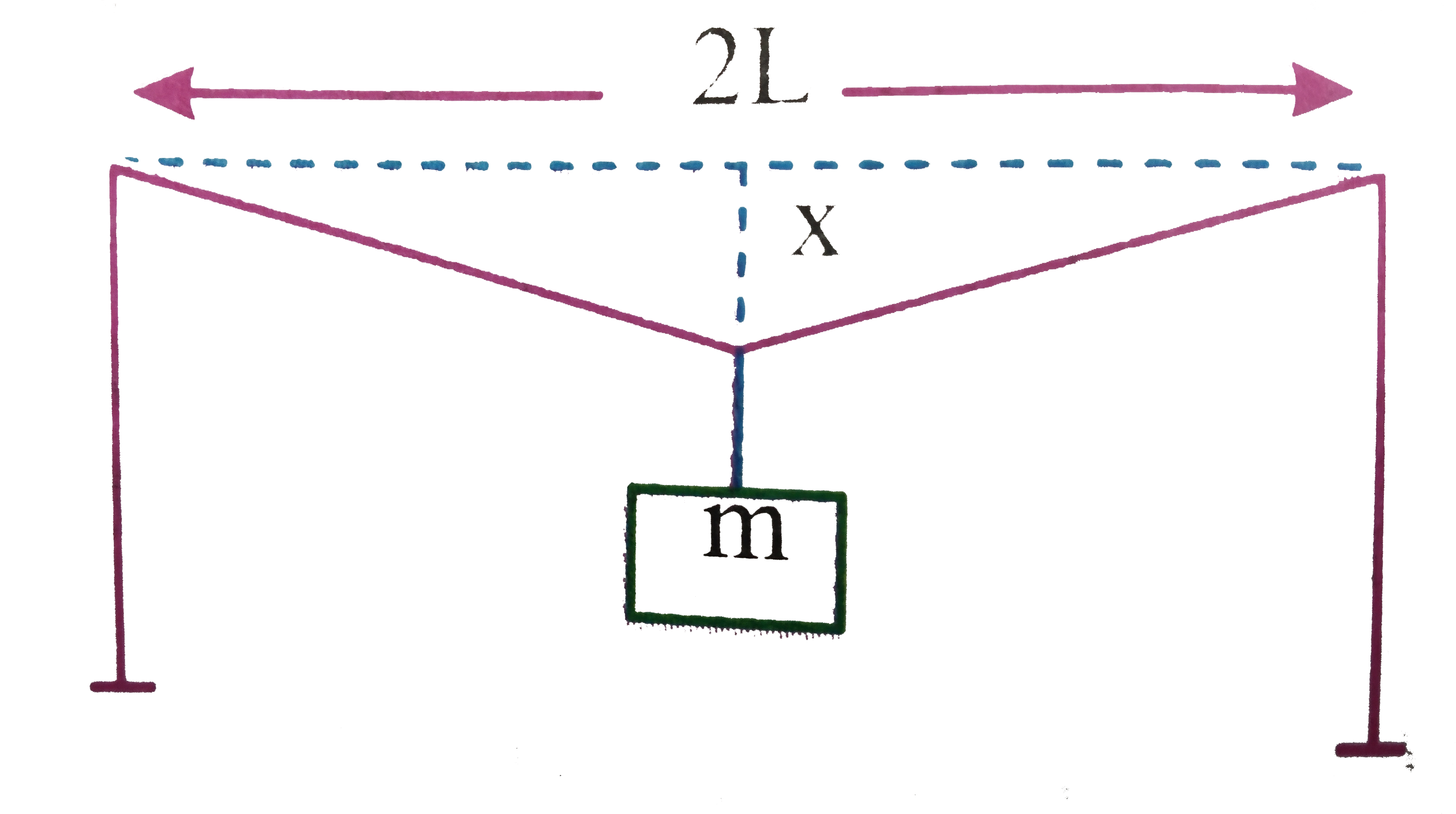
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionThe V – I graph for a wire of copper of length L and cross -section area A is shown in the figure below . The slope of the graph will be
View SolutionThe V – I graph for a wire of copper of length L and cross -section area A is shown in the figure below . The slope of the graph will be

View SolutionA force F doubles the length of wire of cross-section a The Young modulus of wire is
View Solution

