An object of mass 0.2kg executes SHm along the X-axis with frequency of (25/π)Hz. At the point X=0.4m the object has KE0.5J and PE0.4J. The amplitude of oscilation is-
0.06 m
0.04 m
0.05 m
0.25 m
The correct Answer is:A
To solve the problem step by step, we need to find the amplitude of oscillation for an object executing Simple Harmonic Motion (SHM).
Given Data:
- Mass of the object, m=0.2kg
- Frequency, f=25πHz
- Kinetic Energy, KE=0.5J
- Potential Energy, PE=0.4J
- Position, x=0.4m
Step 1: Calculate Total Energy
The total energy E in SHM is the sum of kinetic energy and potential energy:
E=KE+PE
Substituting the values:
E=0.5J+0.4J=0.9J
Step 2: Calculate Angular Frequency ω
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Substituting the value of f:
ω=2π(25π)=50rad/s
Step 3: Use the Total Energy Formula
The total energy in SHM can also be expressed as:
E=12mω2A2
Where A is the amplitude. Rearranging this formula to find A2:
A2=2Emω2
Step 4: Substitute Values to Find Amplitude
Now we can substitute the values of E, m, and ω:
A2=2×0.9J0.2kg×(50rad/s)2
Calculating (50)2:
(50)2=2500
Now substituting this back:
A2=1.80.2×2500=1.8500=0.0036
Step 5: Calculate Amplitude A
Taking the square root to find A:
A=√0.0036=0.06m
Final Answer
The amplitude of oscillation is:
A=0.06mor6cm
- Mass of the object, m=0.2kg
- Frequency, f=25πHz
- Kinetic Energy, KE=0.5J
- Potential Energy, PE=0.4J
- Position, x=0.4m
The total energy E in SHM is the sum of kinetic energy and potential energy:
E=KE+PE
Substituting the values:
E=0.5J+0.4J=0.9J
The angular frequency ω is related to the frequency f by the formula:
ω=2πf
Substituting the value of f:
ω=2π(25π)=50rad/s
The total energy in SHM can also be expressed as:
E=12mω2A2
Where A is the amplitude. Rearranging this formula to find A2:
A2=2Emω2
Now we can substitute the values of E, m, and ω:
A2=2×0.9J0.2kg×(50rad/s)2
Calculating (50)2:
(50)2=2500
Now substituting this back:
A2=1.80.2×2500=1.8500=0.0036
Taking the square root to find A:
A=√0.0036=0.06m
The amplitude of oscillation is:
A=0.06mor6cm
Topper's Solved these Questions
Similar Questions
An object of mass 1kg executes simple harmonic oscillations along the x-axis, with a frequency of 2πHz. At the position x = 1 m, the object has a kinetic energy of 24 J. The amplitude of the oscillation is
View SolutionAn object of mass 0.2 kg executes simple harmonic oscillation along the x-axis with a frequency 25π. At the position x = 0.04m, the object has kinetic energy 0.5J and potential energy 0.4J. amplitude of oscillation is (potential energy is zero mean position).
View SolutionA particle of mass 0.10 kg executes SHM with an amplitude 0.05 m and frequency 20 vib/s. Its energy of oscillation is
View SolutionAn object of mass 5 kg is acted upon by a force that varies with position of the object as shown. If the object starts out from rest at a point x=0. What is its speed at x=50 m.
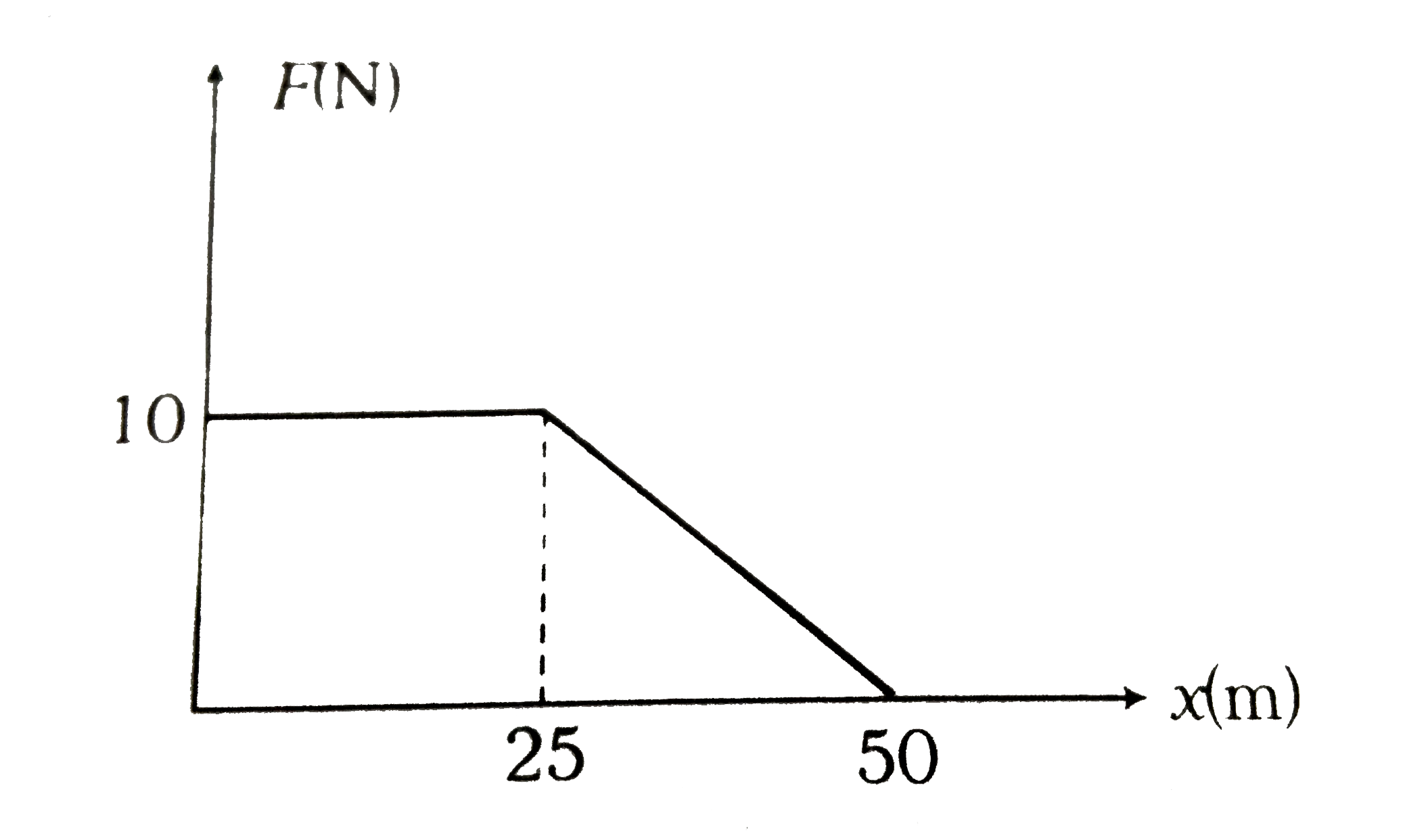 View Solution
View SolutionA object of mass m is suspended from a spring and it executes SHM with frequency n. If the mass is increased 4 times , the new frequency will be
View SolutionA block of mass 0.01 kg is attached to a spring of force constant 10−1Nm−1 . If the energy of oscillation is 10−5 J, find the angular frequency and amplitude of oscillation.
View SolutionA partical of mass 0.2kg executes simple harmonic motion along a path of length 0.2m at the rate of 600oscillations per minute. Assum at t=0. The partical start SHM in positive direction. Find the kinetic potential energies in joules when the displacement is x=A/2 where, A stands for the amplitude.
View SolutionComprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is rough for question, if cofficient of friction is 0.2 in both axis)
Co-ordinates of center of mass where it will stop finally are :-View SolutionIn a standing wave experiment , a 1.2−kg horizontal rope is fixed in place at its two ends (x=0andx=2.0m) and made to oscillate up and down in the fundamental mode , at frequency of 5.0Hz. At t=0 , the point at x=1.0m has zero displacement and is moving upward in the positive direction of y−aξs with a transverse velocity 3.14m/s.
Tension in the rope isView SolutionIn a standing wave experiment , a 1.2−kg horizontal rope is fixed in place at its two ends (x=0andx=2.0m) and made to oscillate up and down in the fundamental mode , at frequency of 5.0Hz. At t=0 , the point at x=1.0m has zero displacement and is moving upward in the positive direction of y−aξs with a transverse velocity 3.14m/s.
Speed of the participating travelling wave on the rope isView Solution
