A particle of mass 0.1 kg is held between two rigid supports by two springs of force constant 8Nm−1and2Nm−1. If the particle is displaced along the direction of length of the springs, its frequency of vibration is
5πHz
8π Hz
2πHz
1π Hz
The correct Answer is:A
To find the frequency of vibration of the particle held between two springs, we can follow these steps:
Step 1: Identify the given data
- Mass of the particle, m=0.1kg
- Spring constant of the first spring, k1=8N/m
- Spring constant of the second spring, k2=2N/m
Step 2: Determine the equivalent spring constant
Since the two springs are in parallel, the equivalent spring constant k can be calculated as:
k=k1+k2
Substituting the values:
k=8N/m+2N/m=10N/m
Step 3: Use the formula for frequency of oscillation
The frequency of oscillation f for a mass-spring system is given by the formula:
f=12π√km
Step 4: Substitute the values into the formula
Now substituting the equivalent spring constant and the mass into the frequency formula:
f=12π√10N/m0.1kg
Step 5: Simplify the expression
Calculating the value inside the square root:
100.1=100
So,
f=12π√100
f=12π×10
f=102π=5πHz
Final Answer
The frequency of vibration of the particle is:
f=5πHz
- Mass of the particle, m=0.1kg
- Spring constant of the first spring, k1=8N/m
- Spring constant of the second spring, k2=2N/m
Since the two springs are in parallel, the equivalent spring constant k can be calculated as:
k=k1+k2
Substituting the values:
k=8N/m+2N/m=10N/m
The frequency of oscillation f for a mass-spring system is given by the formula:
f=12π√km
Now substituting the equivalent spring constant and the mass into the frequency formula:
f=12π√10N/m0.1kg
Calculating the value inside the square root:
100.1=100
So,
f=12π√100
f=12π×10
f=102π=5πHz
The frequency of vibration of the particle is:
f=5πHz
Topper's Solved these Questions
Similar Questions
A mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10cm, then the period of oscillation is
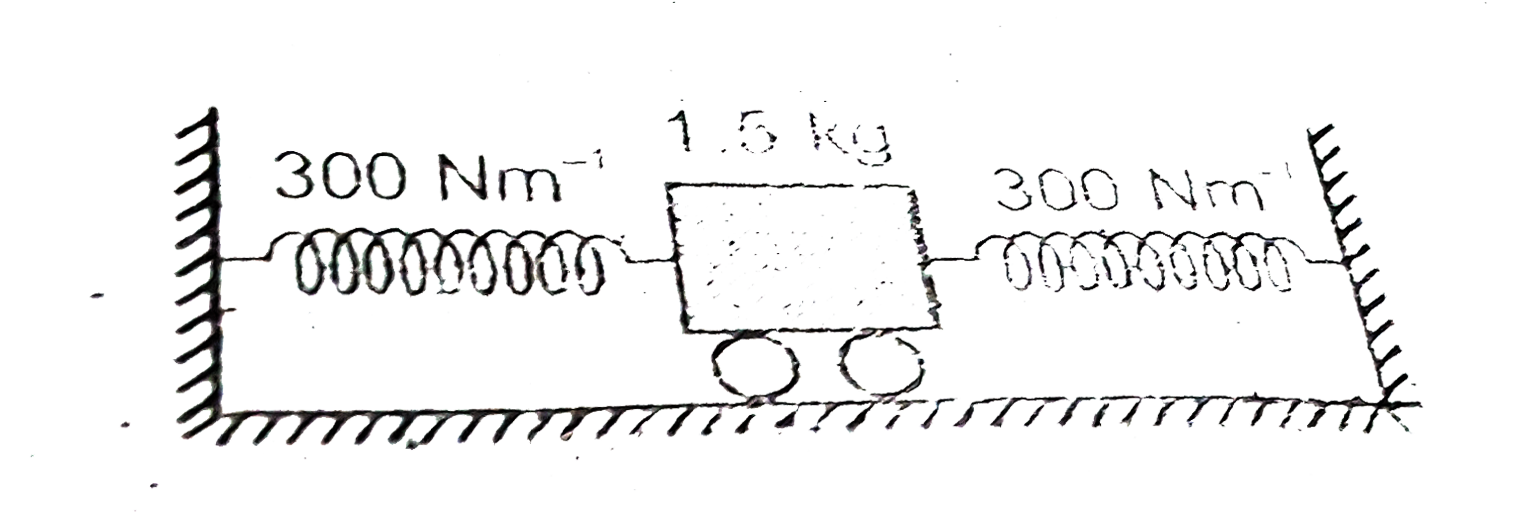
View SolutionA particle of mass 200 g executes a simpel harmonit motion. The resrtoring force is provided by a spring of spring constant 80Nm−1. Find the time period.
View Solution
Knowledge Check
Two springs of spring constants 1000Nm−1 and 2000Nm−1 are stretched with same force. They will have potential energy in the ratio of
A2:1B22:12C1:2D12:22
A mass of 1.5 kg is connected to two identical springs each of force constant 300Nm−1 as shown in the figure. If the mass is displaced from its equilibrium position by 10 cm, then maximum speed of the trolley is
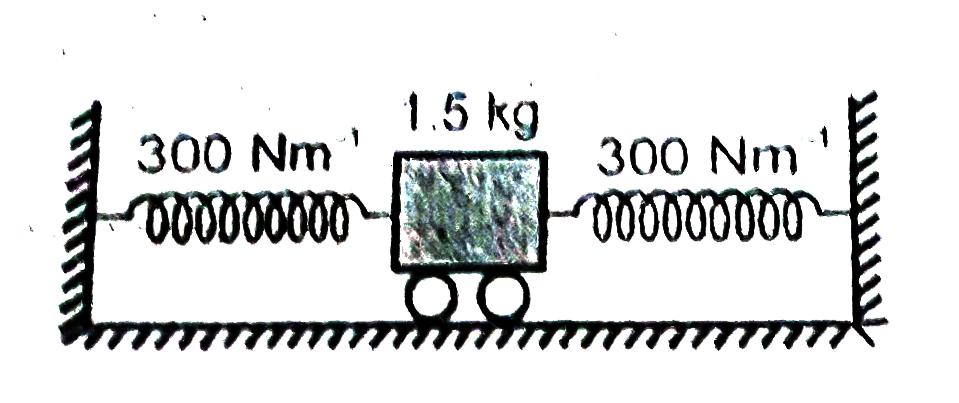
View SolutionA particle of mass 200g executes a simple harmonic motion. The restoring force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA paricle of mass 30kg executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
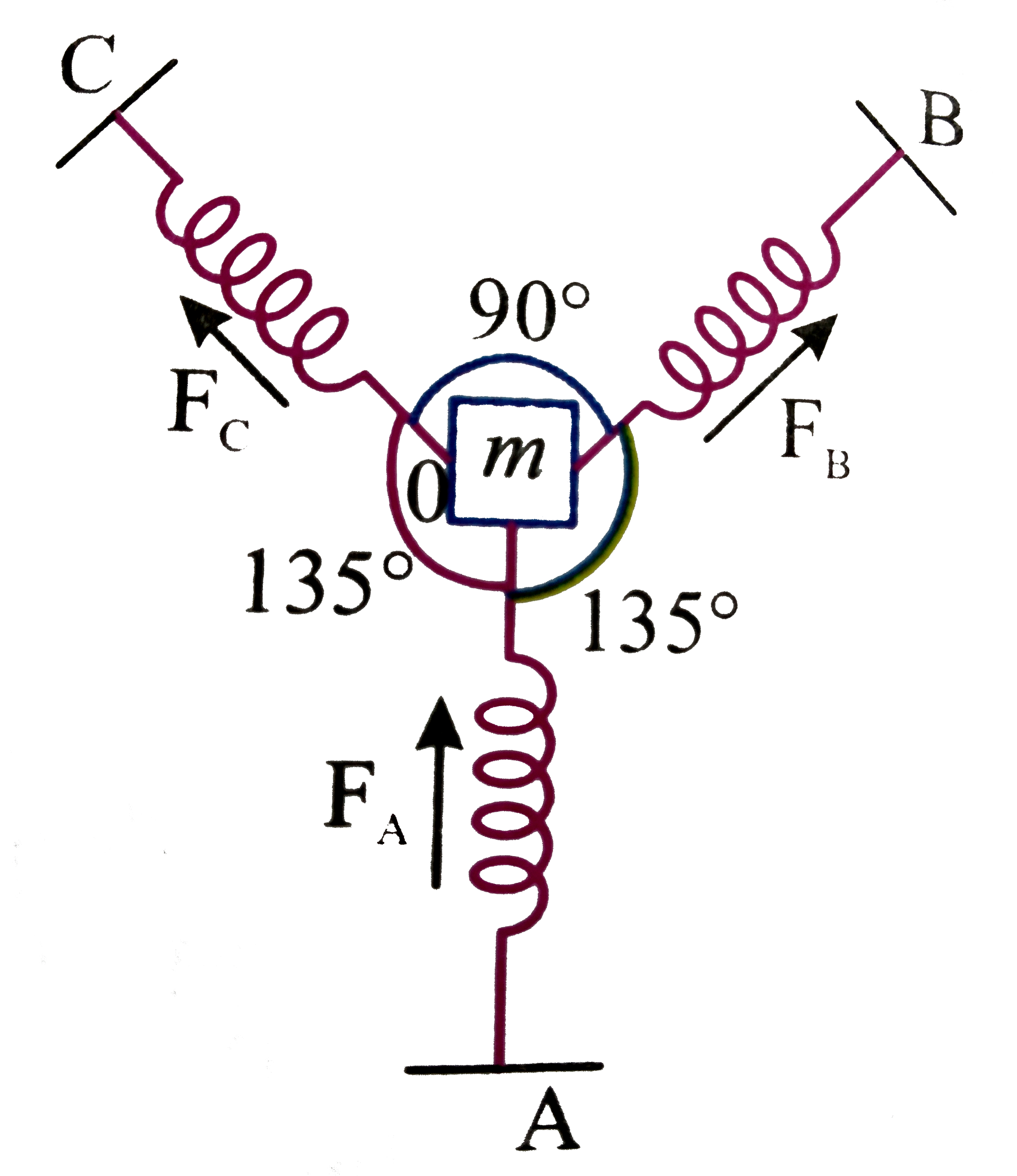
View SolutionA particle of mass 'm' is attached to three identical springs A,B and C each of force constant 'K' as shown in figure. If the particle of mass 'm' is pushed slightly against the spring 'A' and released the period of oscillations is
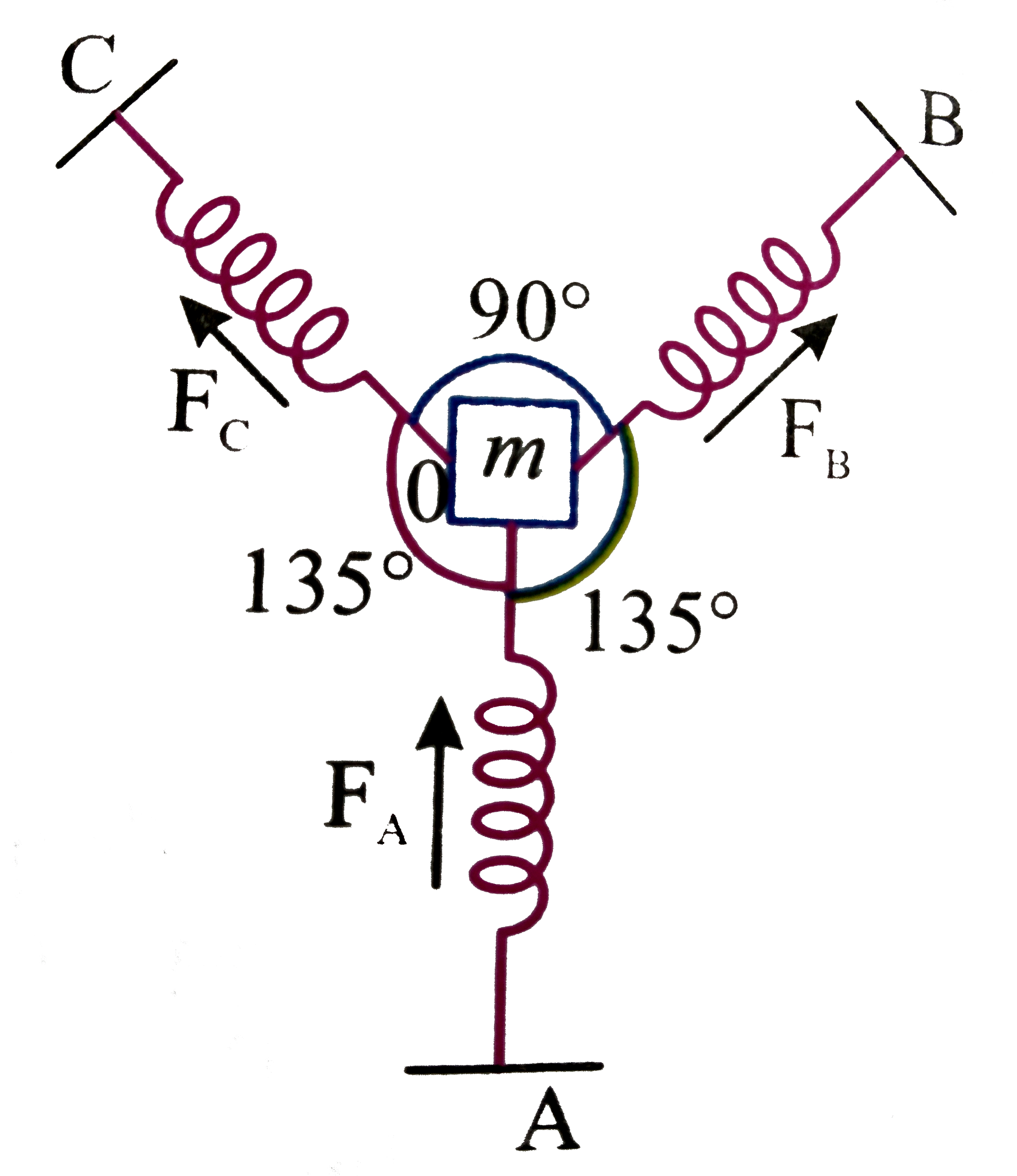
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
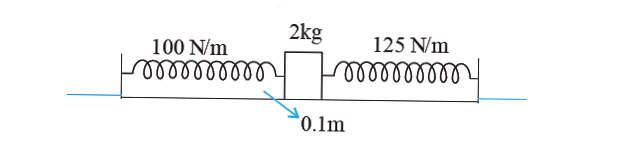
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View Solution

