If E,M,J,andG , respectively , denote energy , mass , angular momentum , and gravitational constant , then EJ2/M5G2 has the dimensions of
length
mass
time
angle
The correct Answer is:D
To find the dimensions of the expression EJ2M5G2, we will first determine the dimensions of each variable involved: energy (E), mass (M), angular momentum (J), and the gravitational constant (G).
Step 1: Determine the dimensions of each variable.
1. Energy (E):
The dimensions of energy are given by:
(E)=(M)(L2)(T−2)=M1L2T−2
2. Mass (M):
The dimensions of mass are:
(M)=M1
3. Angular Momentum (J):
Angular momentum is defined as the product of mass, velocity, and radius. Its dimensions can be expressed as:
(J)=(M)(L)(T−1)⋅(L)=M1L2T−1
4. Gravitational Constant (G):
The dimensions of the gravitational constant can be derived from the formula for gravitational force:
F=Gm1m2r2
Rearranging gives:
(G)=(F)(L2)(M)2=(M)(L)(T−2)(L2)(M)2=M−1L3T−2
Step 2: Substitute the dimensions into the expression.
Now we substitute these dimensions into the expression EJ2M5G2.
1. Calculate J2:
(J2)=(M1L2T−1)2=M2L4T−2
2. Calculate G2:
(G2)=(M−1L3T−2)2=M−2L6T−4
Step 3: Combine the dimensions in the expression.
Now we can substitute these into the expression:
EJ2M5G2=(M1L2T−2)(M2L4T−2)(M5)(M−2L6T−4)
Step 4: Simplify the expression.
Now we simplify the dimensions:
=M1+2L2+4T−2−2M5M−2L6T−4=M3L6T−4M5−2L6T−4=M3L6T−4M3L6T−4=1
Step 5: Conclusion.
The final result gives us:
(M0L0T0)=1
This indicates that the expression has no dimensions, which corresponds to an angle.
Final Answer:
The dimensions of EJ2M5G2 are dimensionless, indicating it can be associated with an angle.
---
The dimensions of energy are given by:
(E)=(M)(L2)(T−2)=M1L2T−2
The dimensions of mass are:
(M)=M1
Angular momentum is defined as the product of mass, velocity, and radius. Its dimensions can be expressed as:
(J)=(M)(L)(T−1)⋅(L)=M1L2T−1
The dimensions of the gravitational constant can be derived from the formula for gravitational force:
F=Gm1m2r2
Rearranging gives:
(G)=(F)(L2)(M)2=(M)(L)(T−2)(L2)(M)2=M−1L3T−2
(J2)=(M1L2T−1)2=M2L4T−2
(G2)=(M−1L3T−2)2=M−2L6T−4
EJ2M5G2=(M1L2T−2)(M2L4T−2)(M5)(M−2L6T−4)
=M1+2L2+4T−2−2M5M−2L6T−4=M3L6T−4M5−2L6T−4=M3L6T−4M3L6T−4=1
(M0L0T0)=1
This indicates that the expression has no dimensions, which corresponds to an angle.
The dimensions of EJ2M5G2 are dimensionless, indicating it can be associated with an angle.
Topper's Solved these Questions
Similar Questions
If E, M, L and G denote energy, mass, angular momentum and gravitational constant repectively then the quantity (E2L2/M5G2) has the dimensions of :-
View SolutionIn the expression P=EL2m−5G−2, E, m, L and G denote energy, mass, angular momentum and gravitational constant, respectively. Show that P is a dimensionless quantity.
View SolutionIf J is the angular momentum and E is the kinetic energy, then J2E has the dimensions of
View Solutionh d G has the dimensions of (h = height , d = density , G = Gravitational constant)
View SolutionIf E = energy , G= gravitational constant, I=impulse and M=mass, then dimensions of GIM2E2 are same as that of
View SolutionThe escape velocity of a sphere of mass m is given by (G= univesal gravitational constant, Me= mass of the earth and Re= radius of the earth)
View SolutionKepler's third law states that square of period revolution (T) of a planet around the sun is proportional to third power of average distance i between sun and planet i.e. T2=Kr3
here K is constant
if the mass of sun and planet are M and m respectively then as per Newton's law of gravitational the force of alteaction between them is F=GMmr2, here G is gravitational constant. The relation between G and K is described as
View SolutionA planet of mass M, has two natural satellites with masses m1 and m2. The radii of their circular orbits are R1 and R2 respectively. Ignore the gravitational force between the satellites. Define v1,L1,K1 and T1 to be, respectively, the orbital speed, angular momentum, kinetic energy and time period of revolution of satellite 1 , and v2,L2,K2 and T2 to be he corresponding quantities of satellite 2. Given m1/m2=2 and R1/R2=1/4, match the ratios in List-I to the numbers in List-II.
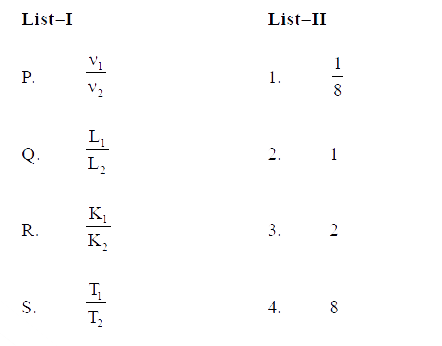
View SolutionThe relation between angular momentum J of a body and rotational kinetic energy is given by J=√2EI. The graph between J and √E will be:
View SolutionThe acceleration due to gravity at a piece depends on the mass of the earth M, radius of the earth R and the gravitational constant G. Derive an expression for g?
View Solution
