Find the momentof inertia of a uniform square plate of mass m and edge a about one of its diagonals.
Ml26
Ml212
Ml23
Ml24
The correct Answer is:B
To find the moment of inertia of a uniform square plate of mass m and edge a about one of its diagonals, we can follow these steps:
Step 1: Understand the Geometry
We have a square plate with mass m and side length a. The diagonals of the square intersect at the center of the square and are perpendicular to each other.
Step 2: Moment of Inertia about the Center of Mass
The moment of inertia of a square plate about an axis perpendicular to its plane and passing through its center of mass is given by the formula:
ICM=ma26
Step 3: Apply the Perpendicular Axis Theorem
The perpendicular axis theorem states that for a planar object, the moment of inertia about an axis perpendicular to the plane (z-axis) is equal to the sum of the moments of inertia about two perpendicular axes (x and y axes) in the plane of the object:
Iz=Ix+Iy
In our case, the two axes in the plane of the square are the diagonals. Since the square is symmetric, we have:
Ix=Iy=Idiagonal
Thus, we can rewrite the equation as:
ICM=Idiagonal+Idiagonal=2Idiagonal
This implies:
Idiagonal=ICM2
Step 4: Substitute the Value of ICM
Now, substituting the value of ICM:
Idiagonal=12(ma26)=ma212
Conclusion
Thus, the moment of inertia of the uniform square plate about one of its diagonals is:
Idiagonal=ma212
Final Answer
The correct option is ma212.
---
We have a square plate with mass m and side length a. The diagonals of the square intersect at the center of the square and are perpendicular to each other.
The moment of inertia of a square plate about an axis perpendicular to its plane and passing through its center of mass is given by the formula:
ICM=ma26
The perpendicular axis theorem states that for a planar object, the moment of inertia about an axis perpendicular to the plane (z-axis) is equal to the sum of the moments of inertia about two perpendicular axes (x and y axes) in the plane of the object:
Iz=Ix+Iy
In our case, the two axes in the plane of the square are the diagonals. Since the square is symmetric, we have:
Ix=Iy=Idiagonal
Thus, we can rewrite the equation as:
ICM=Idiagonal+Idiagonal=2Idiagonal
This implies:
Idiagonal=ICM2
Now, substituting the value of ICM:
Idiagonal=12(ma26)=ma212
Thus, the moment of inertia of the uniform square plate about one of its diagonals is:
Idiagonal=ma212
The correct option is ma212.
Topper's Solved these Questions
Similar Questions
Find the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals.
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge a about one of its diagonals.
View SolutionFind the moment of inertia of a uniform square plate of mass M and edge of length 'l' about its axis passing through P and perpendicular to it.

View SolutionThe radius of gyration of a uniform square plate of mass M and sida about its diagonal is
View SolutionThe moment of inertia of a cube of mass m and side a about one of its edges is equal to
View SolutionFind the moment of inertia of a uniform ring of mass M and radius R about a diameter.
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View SolutionThe moment of inertia of a uniform solid regular tetrahedron of mass m and edge a, about its symmetry axis (i.e and axis passing through on evertex and the centre of the opposite face) is:
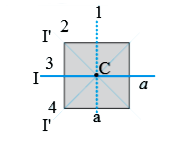
View SolutionIn the figure shown find the moment of inertia of square plate having mass m and sides a. About an axis 2 passing through point C (centre of mass) and in the plane of plate?
View Solution

