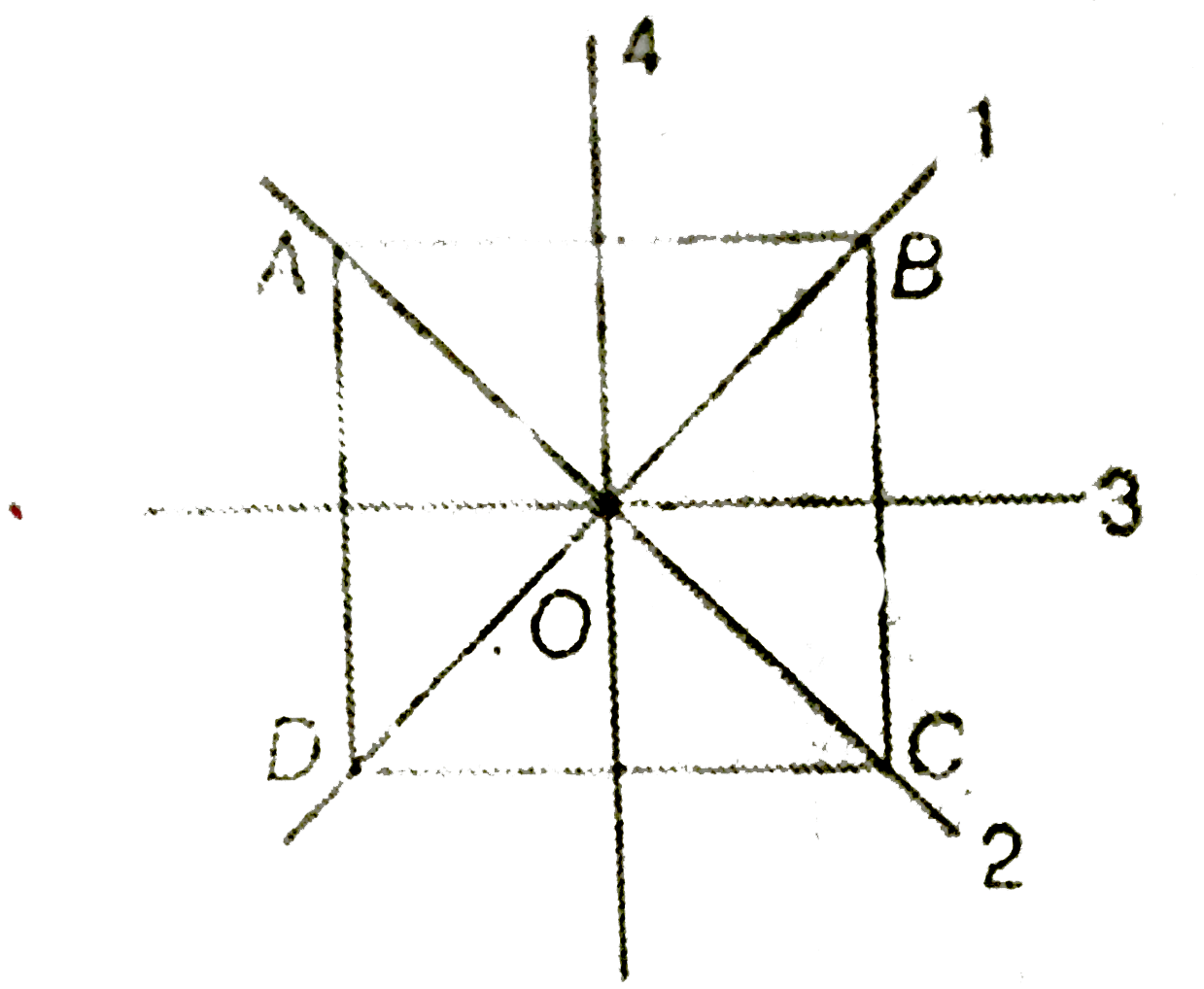
In the figure shown find the moment of inertia of square plate having mass m and sides a. About an axis 2 passing through point C (centre of mass) and in the plane of plate?

Video Solution

Text Solution

Verified by Experts

Using perpendicular axis theorems $I_{C} = I_{4} + I_{2} = 21$ , Using perpendicular theorems $I_{C} = I_{3} + I_{1} = 21$ 2I.=21 I.=I $I C = 21 = \frac{m a^{2}}{6} \Rightarrow I . \frac{m a^{2}}{12}$ .

Updated on:21/07/2023

|

Class 12 PHYSICS SYSTEM OF A PARTICLES & ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Find the momentof inertia of a uniform square plate of mass m and edge a about one of its diagonals.
A $\frac{M l^{2}}{6}$
B $\frac{M l^{2}}{12}$
C $\frac{M l^{2}}{3}$
D $\frac{M l^{2}}{4}$

VMC MODULES ENGLISH-SYSTEM OF A PARTICLES & ROTATIONAL MOTION-IN-CHAPTER EXERCISE F

Home
Ask Doubt
Profile