A uniform rope of length 12 mm and mass 6 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope. What is the wavelength of the pulse when it reaches the top of the rope?
0.06 m
0.03 m
0.12 m
0.09 m
The correct Answer is:C
To solve the problem step by step, we will follow these calculations:
Step 1: Calculate the Linear Mass Density (μ)
The linear mass density (μ) of the rope is calculated using the formula:
μ=mL
where:
- m=6kg (mass of the rope)
- L=12mm=0.012m (length of the rope)
Calculating:
μ=6kg0.012m=500kg/m
Step 2: Calculate the Tension at the Lower End (T1)
At the lower end of the rope, the tension (T1) is due to the weight of the block attached:
T1=mblock⋅g
where:
- mblock=2kg
- g=9.81m/s2 (acceleration due to gravity)
Calculating:
T1=2kg⋅9.81m/s2=19.62N
Step 3: Calculate the Tension at the Upper End (T2)
At the upper end of the rope, the tension (T2) is the sum of the weight of the rope and the block:
T2=(mrope+mblock)⋅g
where:
- mrope=6kg
Calculating:
T2=(6kg+2kg)⋅9.81m/s2=8⋅9.81N=78.48N
Step 4: Calculate the Velocity of the Pulse at Both Ends
The velocity (v) of a wave on a string is given by:
v=√Tμ
Calculating the velocity at the lower end (v1):
v1=√T1μ=√19.62N500kg/m=√0.03924≈0.198m/s
Calculating the velocity at the upper end (v2):
v2=√T2μ=√78.48N500kg/m=√0.15696≈0.396m/s
Step 5: Calculate the Frequency of the Pulse
The frequency (f) of the wave can be calculated using the wavelength (λ) and velocity (v):
f=vλ
Using the wavelength at the lower end (λ1 = 0.06 m):
f=v1λ1=0.198m/s0.06m≈3.3Hz
Step 6: Calculate the Wavelength at the Upper End (λ2)
Using the frequency calculated and the velocity at the upper end:
λ2=v2f=0.396m/s3.3Hz≈0.12m
Final Answer
The wavelength of the pulse when it reaches the top of the rope is approximately:
λ2≈0.12m
---
The linear mass density (μ) of the rope is calculated using the formula:
μ=mL
where:
- m=6kg (mass of the rope)
- L=12mm=0.012m (length of the rope)
μ=6kg0.012m=500kg/m
At the lower end of the rope, the tension (T1) is due to the weight of the block attached:
T1=mblock⋅g
where:
- mblock=2kg
- g=9.81m/s2 (acceleration due to gravity)
T1=2kg⋅9.81m/s2=19.62N
At the upper end of the rope, the tension (T2) is the sum of the weight of the rope and the block:
T2=(mrope+mblock)⋅g
where:
- mrope=6kg
T2=(6kg+2kg)⋅9.81m/s2=8⋅9.81N=78.48N
The velocity (v) of a wave on a string is given by:
v=√Tμ
Calculating the velocity at the lower end (v1):
v1=√T1μ=√19.62N500kg/m=√0.03924≈0.198m/s
v2=√T2μ=√78.48N500kg/m=√0.15696≈0.396m/s
The frequency (f) of the wave can be calculated using the wavelength (λ) and velocity (v):
f=vλ
Using the wavelength at the lower end (λ1 = 0.06 m):
f=v1λ1=0.198m/s0.06m≈3.3Hz
Using the frequency calculated and the velocity at the upper end:
λ2=v2f=0.396m/s3.3Hz≈0.12m
The wavelength of the pulse when it reaches the top of the rope is approximately:
λ2≈0.12m
Topper's Solved these Questions
Similar Questions
A uniform rope of length 10 cm and mass 4 kg hangs vertically from a rigid support. A block of mass 2 kg is attached to the free end of the rope. A transverse pulse of wavelength 0.06 m is produced at the lower end of the rope, what is the wavelength of the pulse when it reaches the top of the rope?
View SolutionA uniform rope of legnth L and mass m1 hangs vertically from a rigid support. A block of mass m2 is attached to the free end of the rope. A transverse pulse of wavelength λ1 is produced at the lower end of the rope. The wavelength of the pulse when it reaches the top of the rope is λ2. The ratio λ2λ1 is
View SolutionA uniform rope of elngth l and mass m hangs vertically from a rigid support. A block of mass m is attached to the free end of the rope. A transverse pulse of wavelength λ is produced at the lower end of the rope. The wavelength of the pulse, when it reaches the top of the rope. is aλ. Find a2
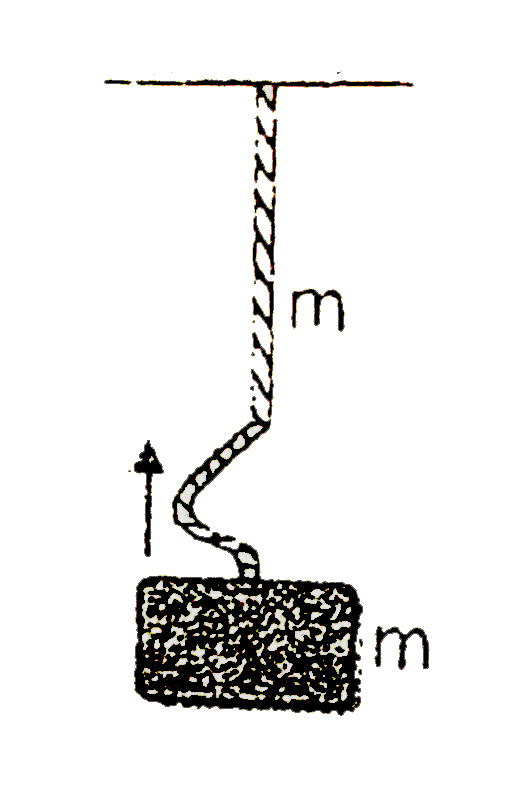
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View SolutionA uniform rope of length 12 m and mass 4 kg is hung vertically from a rigid support transverse wave pulse is produced at lower end. The speed of the wave pulse al x = 2.5 m from lower and will be kg=10 m/s)
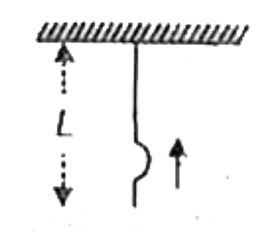
View SolutionA pulse is generated at lower end to a hanging rope of uniform density and length L. The speed of the pulse when it reaches the mid point of rope is
View SolutionA Uniform rope having mass m hags vertically from a rigid support. A transverse wave pulse is produced at the lower end. The speed v of wave pulse varies with height h from the lower end as
View SolutionA thick uniform rope of length L is hanging from a rigid support. A transverse wave of wavelength λ0 is set up in the middle of the rope. The wavelength of the wave as it reaches the top most point is
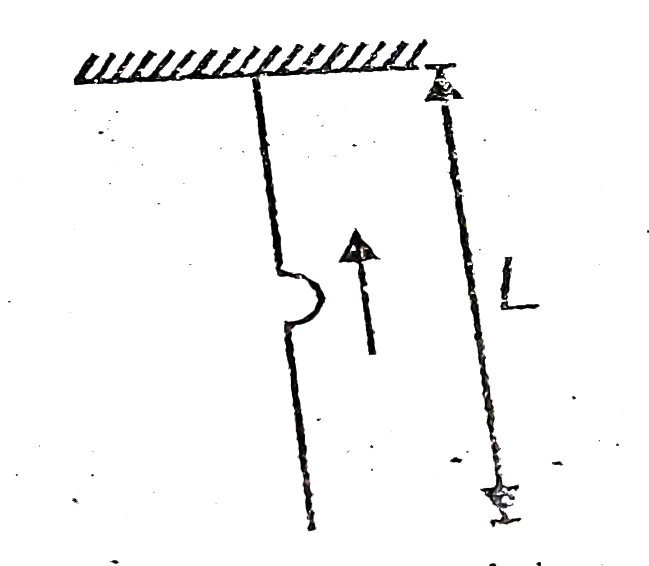
View SolutionA wire of length L, is hanging vertically from a rigid support. If a transverse wave pulse is generated at the free end of wire then which of the following statement is wrong
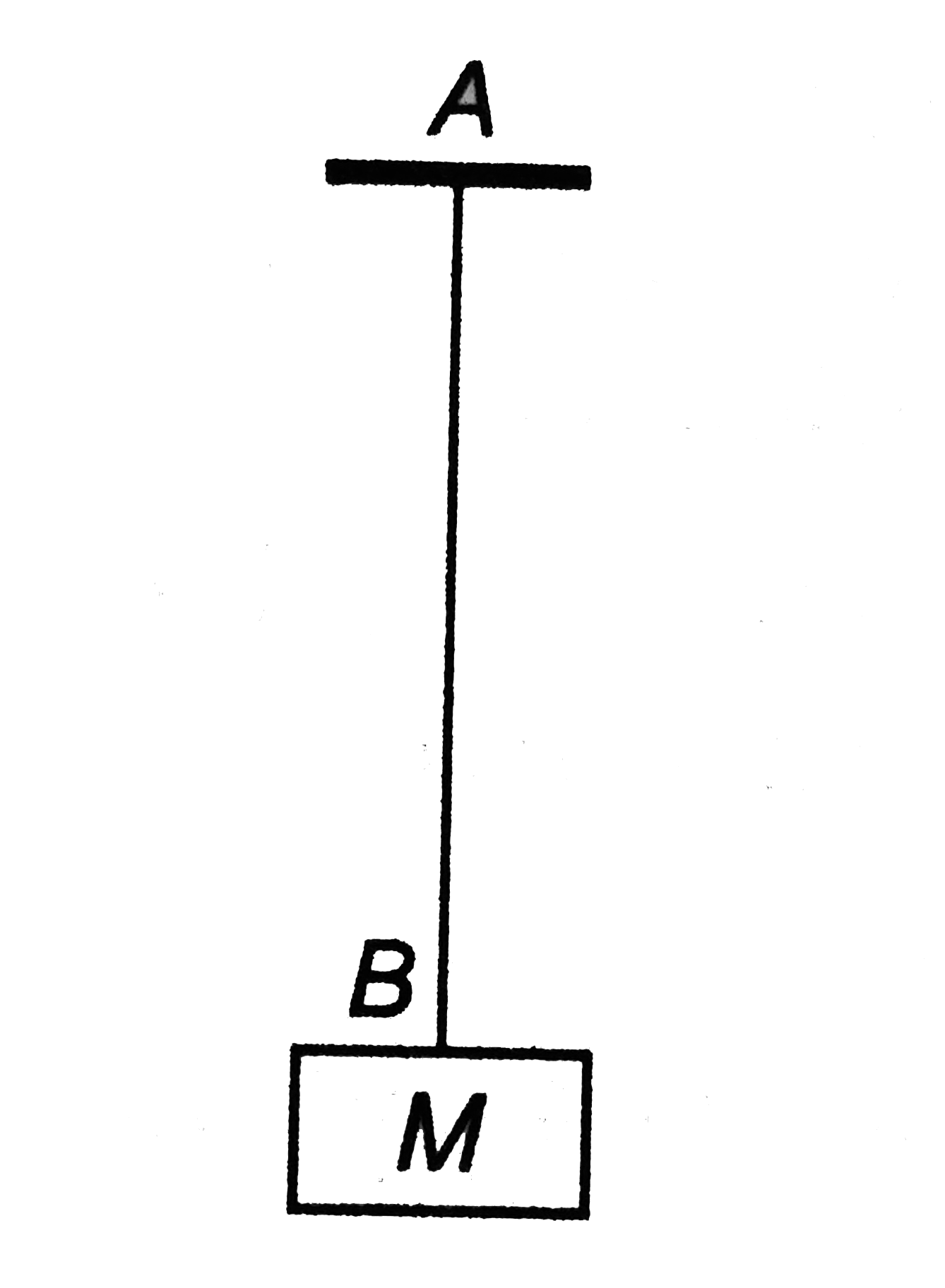
View SolutionA block of mass M=2kg is suspended from a string AB of mass 6kg as shown in figure. A transverse wave pulse of wavelength λ0 is produced at point B. find its wavelength while reaching at point A.
View Solution

