The relation between Y. η and B is
1Y=13η+19B
9Y=1η+3B
1η=1B+1Y
9Y=3η+1B
The correct Answer is:D
To find the relation between Young's modulus (Y), rigidity modulus (η), and bulk modulus (B), we can follow these steps:
Step 1: Write down the definitions
Young's modulus (Y), rigidity modulus (η), and bulk modulus (B) are defined as follows:
- Young's modulus (Y) is defined as the ratio of tensile stress to tensile strain.
- Rigidity modulus (η) is defined as the ratio of shear stress to shear strain.
- Bulk modulus (B) is defined as the ratio of volumetric stress to the change in volume strain.
Step 2: Use the relationships between the moduli
From material mechanics, we have the following relationships:
1. Y=2η(1+u) (where u is Poisson's ratio)
2. Y=3B(1−2u)
Step 3: Rearrange the equations
We can rearrange these equations to express them in terms of Y, η, and B.
From the first equation, we can express η:
η=Y2(1+u)(Equation 1)
From the second equation, we can express B:
B=Y3(1−2u)(Equation 2)
Step 4: Substitute the expressions into a single equation
To find a relation involving all three moduli, we can substitute the expressions for η and B into a single equation. We can manipulate the equations as follows:
1. Substitute η from Equation 1 into the relation 9Y=3η+1B:
9Y=3(2(1+u))Y+1Y3(1−2u)
2. Simplifying this gives:
9Y=6(1+u)Y+3(1−2u)Y
Step 5: Combine the terms
Now, combine the terms on the right-hand side:
9Y=6(1+u)+3(1−2u)Y
This simplifies to:
9Y=9−3uY
Step 6: Final relation
Thus, we can conclude that:
9Y=3η+1B
Final Answer
The relation between Young's modulus (Y), rigidity modulus (η), and bulk modulus (B) is:
9Y=3η+1B
Young's modulus (Y), rigidity modulus (η), and bulk modulus (B) are defined as follows:
- Young's modulus (Y) is defined as the ratio of tensile stress to tensile strain.
- Rigidity modulus (η) is defined as the ratio of shear stress to shear strain.
- Bulk modulus (B) is defined as the ratio of volumetric stress to the change in volume strain.
From material mechanics, we have the following relationships:
1. Y=2η(1+u) (where u is Poisson's ratio)
2. Y=3B(1−2u)
We can rearrange these equations to express them in terms of Y, η, and B.
From the first equation, we can express η:
η=Y2(1+u)(Equation 1)
From the second equation, we can express B:
B=Y3(1−2u)(Equation 2)
To find a relation involving all three moduli, we can substitute the expressions for η and B into a single equation. We can manipulate the equations as follows:
1. Substitute η from Equation 1 into the relation 9Y=3η+1B:
9Y=3(2(1+u))Y+1Y3(1−2u)
2. Simplifying this gives:
9Y=6(1+u)Y+3(1−2u)Y
Now, combine the terms on the right-hand side:
9Y=6(1+u)+3(1−2u)Y
This simplifies to:
9Y=9−3uY
Thus, we can conclude that:
9Y=3η+1B
The relation between Young's modulus (Y), rigidity modulus (η), and bulk modulus (B) is:
9Y=3η+1B
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - HOTS
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - STRESS-STRAIN CURVE
5 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
Knowledge Check
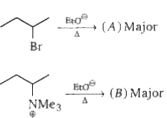
Relation between (A) and (B) is :AG.IBPositional isomerCEnantiomerDChain isomerFor nitrogen Cp−CV=x and for argon CP−CV=Y. The relation between x and y is given by a) x = y b) x = 7y c) y = 7x d) x = 1/2 y
Ax=yBx=7yCy=7xDx=12y
P(A∪B)=P(A∩B) if and only if the relation between P(A) and P(B) is …………
View SolutionIf the relation between A and B is known to be to the form : B=k×n4 , what is the value of ( k + n) ? The following data was observed between the variable A and B :
AB324448596
View SolutionThe relation between algae and fungi in a lichen is
View SolutionWhat is relation between
_S01_028_Q01.png)
View SolutionRelation between (A) and (B) is
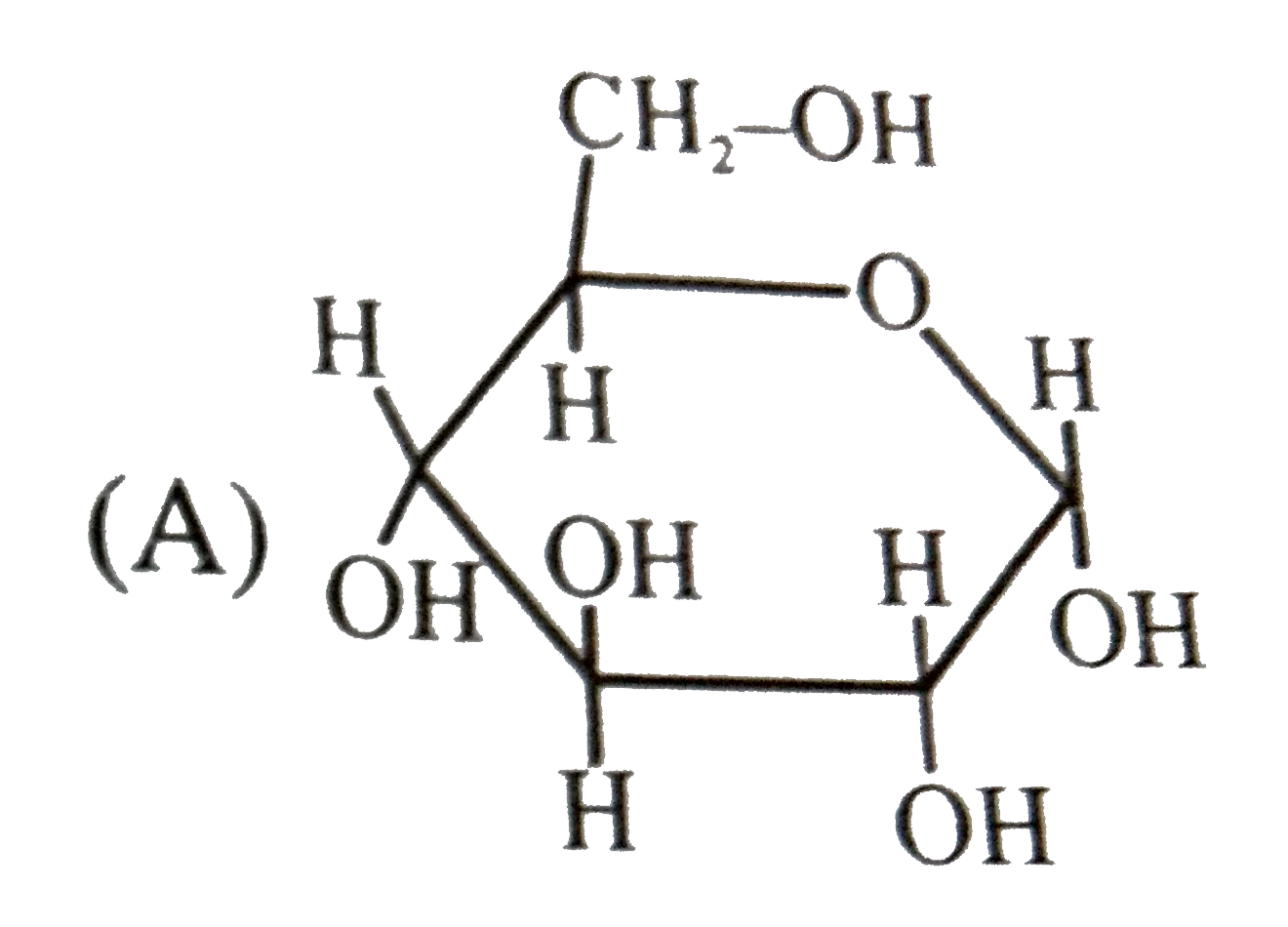
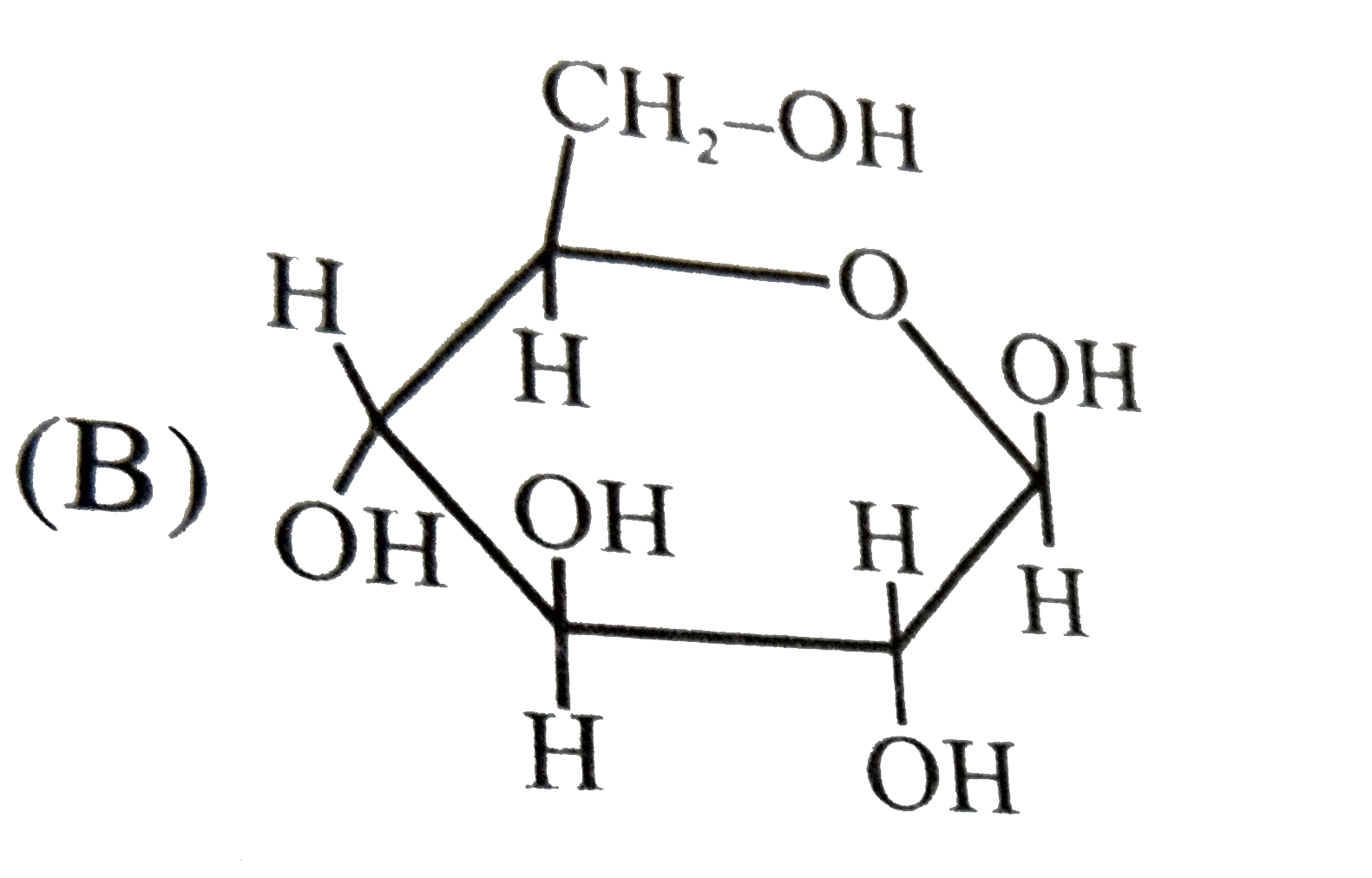
View SolutionFind the relation between a and b if the lines 3x−by+5=0 and ax+y=2 parallel.
View Solution
