In the question number 51 , the potential at the centre is
−2Gml
3√2Gml
−2√2Gml
−4√2Gml
The correct Answer is:D
To find the gravitational potential at the center of a square with four equal masses placed at its vertices, we can follow these steps:
Step 1: Understand the Setup
We have a square with side length L and four masses, each of mass m, positioned at the vertices of the square. We need to calculate the gravitational potential at the center of this square.
Step 2: Determine the Distance from the Center to a Vertex
The distance from the center of the square to any vertex can be calculated using the Pythagorean theorem. The center divides the square into four equal parts, and the distance from the center to a vertex (let's denote it as r) is given by:
r=L√2
This is because each half of the square forms a right triangle with sides of length L2.
Step 3: Write the Formula for Gravitational Potential
The gravitational potential V due to a single mass m at a distance r is given by:
V=−Gmr
where G is the gravitational constant.
Step 4: Calculate the Total Potential at the Center
Since there are four masses contributing to the potential at the center, the total potential Vtotal is the sum of the potentials due to each mass:
Vtotal=VA+VB+VC+VD
Substituting the expression for potential:
Vtotal=−Gmr−Gmr−Gmr−Gmr=−4⋅Gmr
Now substituting r=L√2:
Vtotal=−4⋅GmL√2=−4⋅Gm√2L
Step 5: Final Expression for the Potential
Thus, the potential at the center of the square is:
Vtotal=−4√2GmL
Conclusion
The potential at the center of the square formed by four masses at its vertices is:
Vcenter=−4√2GmL
We have a square with side length L and four masses, each of mass m, positioned at the vertices of the square. We need to calculate the gravitational potential at the center of this square.
The distance from the center of the square to any vertex can be calculated using the Pythagorean theorem. The center divides the square into four equal parts, and the distance from the center to a vertex (let's denote it as r) is given by:
r=L√2
This is because each half of the square forms a right triangle with sides of length L2.
The gravitational potential V due to a single mass m at a distance r is given by:
V=−Gmr
where G is the gravitational constant.
Since there are four masses contributing to the potential at the center, the total potential Vtotal is the sum of the potentials due to each mass:
Vtotal=VA+VB+VC+VD
Substituting the expression for potential:
Vtotal=−Gmr−Gmr−Gmr−Gmr=−4⋅Gmr
Now substituting r=L√2:
Vtotal=−4⋅GmL√2=−4⋅Gm√2L
Thus, the potential at the center of the square is:
Vtotal=−4√2GmL
The potential at the center of the square formed by four masses at its vertices is:
Vcenter=−4√2GmL
Topper's Solved these Questions
- GRAVITATIONBook:NCERT FINGERTPS ENGLISHChapter:GRAVITATIONExercise:Escape Speed
Explore 7 Videos
- GRAVITATIONBook:NCERT FINGERTPS ENGLISHChapter:GRAVITATIONExercise:Earth Satellite
Explore 4 Videos
- GRAVITATIONBook:NCERT FINGERTPS ENGLISHChapter:GRAVITATIONExercise:Acceleration due to gravity below and above the surface of earth
Explore 8 Videos
- KINETIC THEORYBook:NCERT FINGERTPS ENGLISHChapter:KINETIC THEORYExercise:Assertion And Reason
Explore 10 Videos
Similar Questions
If the electric potential of the inner shell is 10V and that of the outer shel is 5V, then the potential at the centre will be

View SolutionA solid sphere of radius R is charged uniformly through out the volume. At what distance from its surface is the electric potential 1/4 of the potential at the centre?
View Solution
Knowledge Check
In the question number 7, the rate of change of potential difference between the plates is
A2.41×109Vs−1B1.87×109Vs−1C3.2×10−4Vs−1D4.5×10−4Vs−1In the question number 96, the number of turns in the secondary is
A20B80C120D160
There is a uniformly charged non conducting solid sphere made of amterial of dielectric constant one. If electric potenial at infinity be zero. Then the potential at its surface is V. if we take electric potential at its surface to be zero. Then the potential at the centre will be
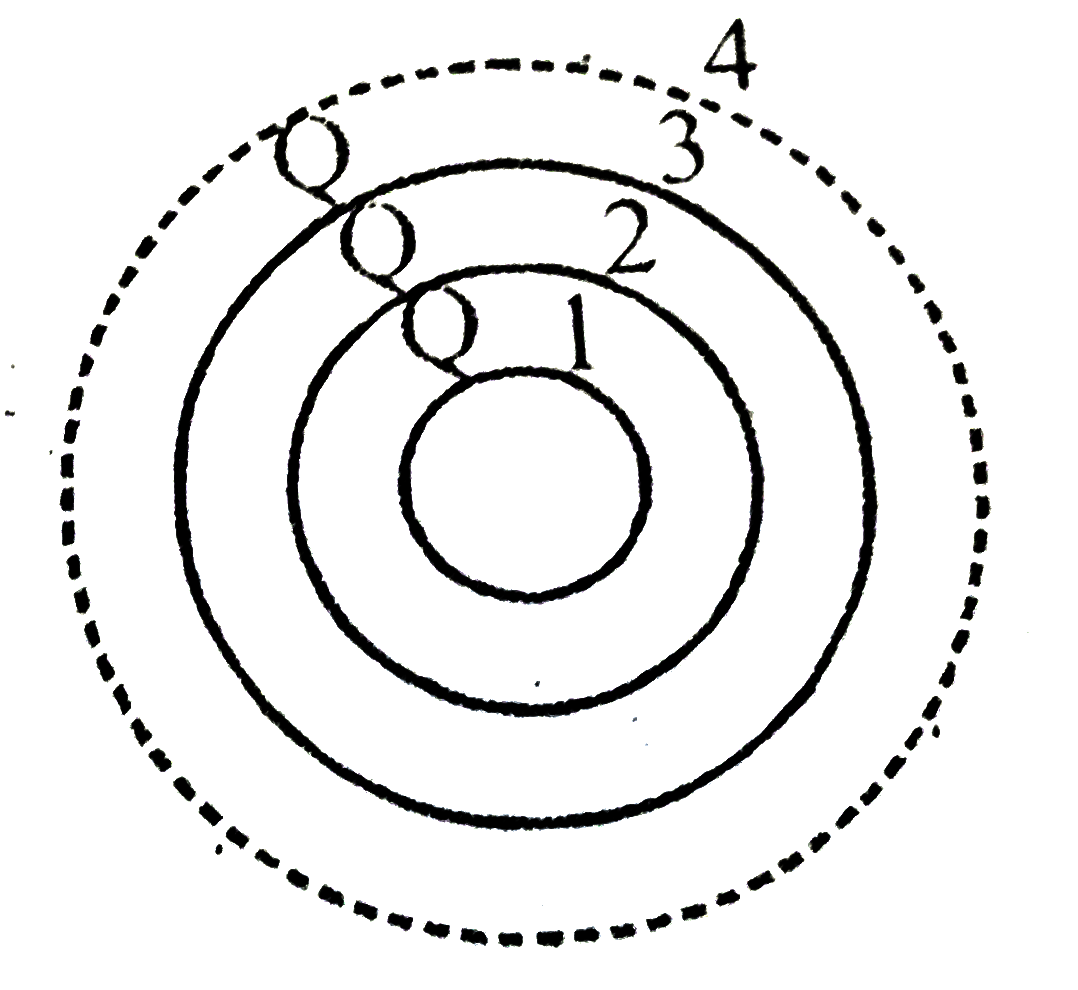
View SolutionAn infinite number of concentric rings carry a charge Q each alternately positive and negative.
Their radii are 1, 2, 4, 8..... meters in gometric progression as shown in the figure. The potential at the centre of the rings will be
View SolutionIf the electric potential of the inner metal sphere is 10 volt & that of the outer shell is 5 volt then the potential at the centre will be
View SolutionA hollow metal sphere of radius 5cm is charged so that the potential on its surface is 10V. The potential at the centre of the sphere is
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View SolutionA conducting sphere of radius R2 has a spherical cavity of radius R1 which is non concentric with the sphere. A point charge q1 is placed at a distance r from the centre of the cavity. For this arrangement, answer the following questions.
Electric potential at the centre of the cavity will be :
View Solution

