Question

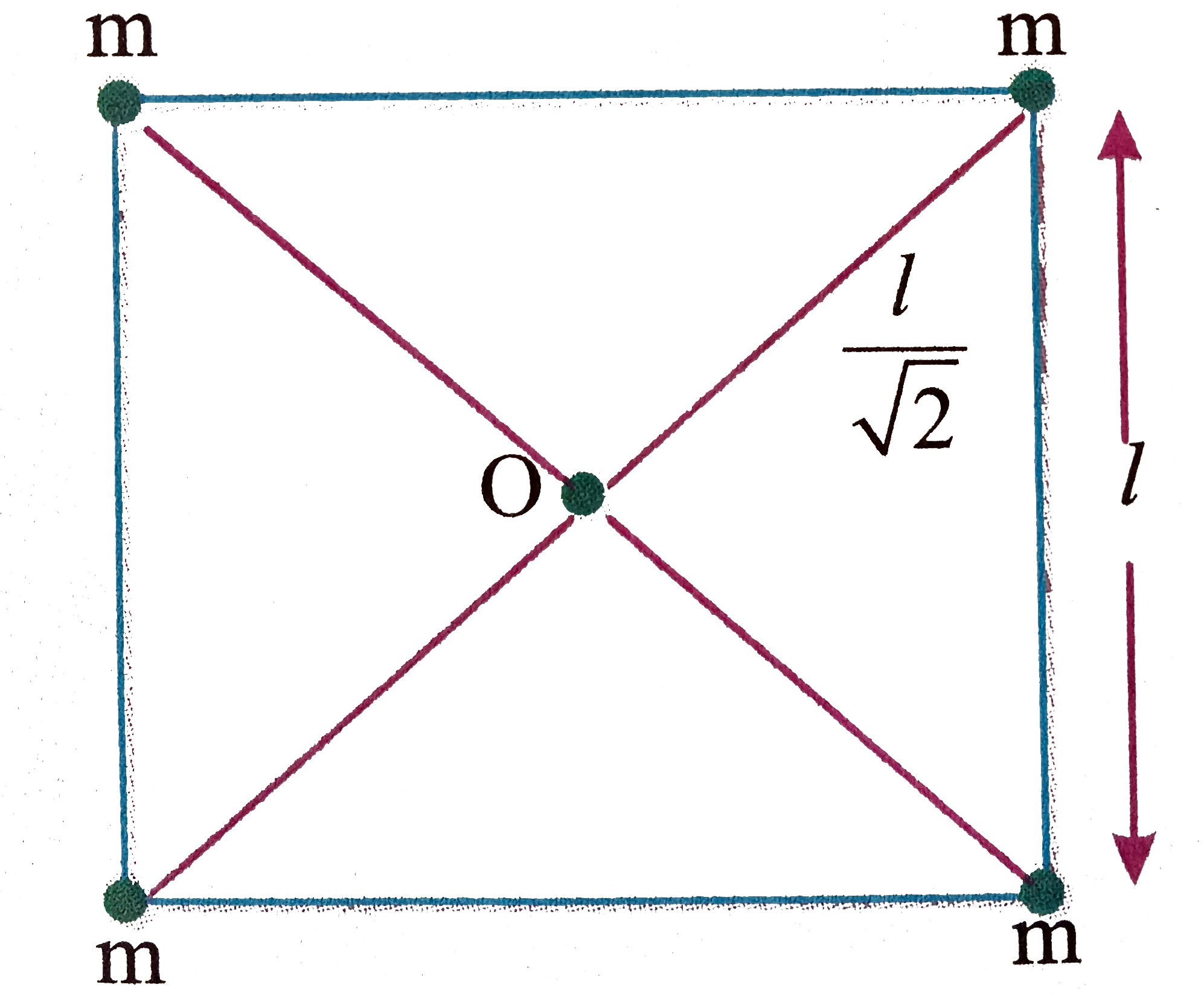
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is

Options

A. `-(sqrt(2)Gm^(2))/(l)(2-(1)/(sqrt(2)))`
B. `-(2Gm^(2))/(l)(2+(1)/(sqrt(2)))`
C. `-(sqrt(2)Gm^(2))/(l)(sqrt(2)-(1)/(sqrt(2)))`
D. `-(2Gm^(2))/(l)(sqrt(2)-(1)/(sqrt(2)))`

Answer

B

Explanation

To find the gravitational potential at the center of a square formed by four particles, each of mass $$m$$, placed at the vertices of the square with side length $$l$$, we can follow these steps:

Step 1: Determine the distance from the center to a vertex
The center of the square is equidistant from all four vertices. We can find this distance using the Pythagorean theorem. The distance \( r \) from the center to any vertex (say vertex A) can be calculated as follows:

\( r = \frac{l}{\sqrt{2}} \)

This is because the distance from the center to a vertex forms a right triangle with half the side length as one leg and half the other side length as the other leg.

Step 2: Calculate the gravitational potential due to one mass
The gravitational potential \( V \) due to a single mass \( m \) at a distance \( r \) is given by the formula:

\( V = -\frac{Gm}{r} \)

Substituting \( r = \frac{l}{\sqrt{2}} \):

\( V_A = -\frac{Gm}{\frac{l}{\sqrt{2}}} = -\frac{Gm \sqrt{2}}{l} \)

Step 3: Calculate the total gravitational potential at the center
Since there are four identical masses at the vertices, the total potential at the center \( V_O \) is the sum of the potentials due to each mass:

\( V_O = V_A + V_B + V_C + V_D \)

Since \( V_A = V_B = V_C = V_D \):

\( V_O = 4 \times V_A = 4 \left(-\frac{Gm \sqrt{2}}{l}\right) \)

Step 4: Simplify the expression
Now, we can simplify the expression for the total potential:

\( V_O = -\frac{4Gm \sqrt{2}}{l} \)

Final Answer
Thus, the gravitational potential at the center of the square is:

\( V_O = -\frac{4Gm \sqrt{2}}{l} \)

---