Four particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
The correct Answer is:A, B, D
To find the gravitational potential energy of a system of four particles each of mass m located at the vertices of a square of side a, we can follow these steps:
Step 1: Identify the pairs of particles and their distances
In a square configuration with four particles, we have:
- Four pairs of particles that are separated by a distance a (the sides of the square).
- Two pairs of particles that are separated by a distance √2a (the diagonals of the square).
Step 2: Calculate the potential energy for pairs separated by distance a
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
For the pairs separated by distance a:
- There are 4 such pairs.
- The potential energy for one pair is:
Ua=−Gmma=−Gm2a
Thus, the total potential energy for the four pairs is:
Utotala=4⋅Ua=4(−Gm2a)=−4Gm2a
Step 3: Calculate the potential energy for pairs separated by distance √2a
For the pairs separated by distance √2a:
- There are 2 such pairs.
- The potential energy for one pair is:
U√2=−Gmm√2a=−Gm2√2a
Thus, the total potential energy for these two pairs is:
Utotal√2=2⋅U√2=2(−Gm2√2a)=−2Gm2√2a
Step 4: Combine the total potential energies
Now we can combine the total potential energies from both sets of pairs:
Utotal=Utotala+Utotal√2
Substituting the values we found:
Utotal=−4Gm2a−2Gm2√2a
Step 5: Simplify the expression
To simplify, we can factor out −Gm2a:
Utotal=−Gm2a(4+2√2)
Since 2√2=√2, we can rewrite it as:
Utotal=−Gm2a(4+√2)
Final Answer
Thus, the gravitational potential energy of the system of four particles is:
Utotal=−Gm2a(4+√2)
In a square configuration with four particles, we have:
- Four pairs of particles that are separated by a distance a (the sides of the square).
- Two pairs of particles that are separated by a distance √2a (the diagonals of the square).
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
For the pairs separated by distance a:
- There are 4 such pairs.
- The potential energy for one pair is:
Ua=−Gmma=−Gm2a
Thus, the total potential energy for the four pairs is:
Utotala=4⋅Ua=4(−Gm2a)=−4Gm2a
For the pairs separated by distance √2a:
- There are 2 such pairs.
- The potential energy for one pair is:
U√2=−Gmm√2a=−Gm2√2a
Thus, the total potential energy for these two pairs is:
Utotal√2=2⋅U√2=2(−Gm2√2a)=−2Gm2√2a
Now we can combine the total potential energies from both sets of pairs:
Utotal=Utotala+Utotal√2
Substituting the values we found:
Utotal=−4Gm2a−2Gm2√2a
To simplify, we can factor out −Gm2a:
Utotal=−Gm2a(4+2√2)
Since 2√2=√2, we can rewrite it as:
Utotal=−Gm2a(4+√2)
Thus, the gravitational potential energy of the system of four particles is:
Utotal=−Gm2a(4+√2)
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.6
3 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.7
5 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.4
4 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
Eight particles of mass 'm' each are placed at the verties of a cube of side 'a' . Find gravitational potential energy of this system .
 .
.
View SolutionFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
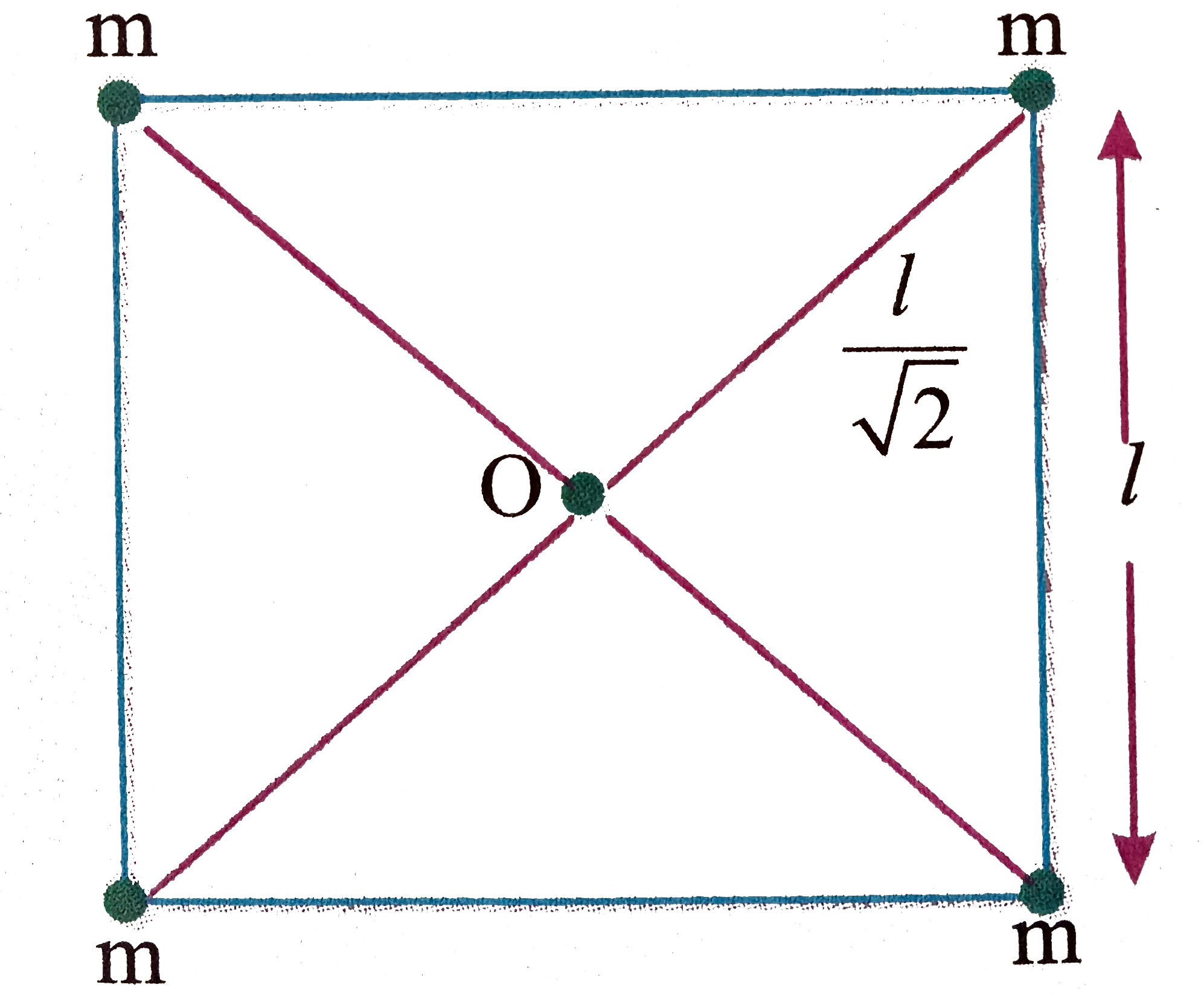
View Solution
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)
Find the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View SolutionFour particles each of mass 'm' are kept at the four corners of a square of edge 'a'. Find the moment of inertia of the system about a line perpendicular to the plane of the square and passing through the center of the square.
View SolutionThree masses of 1kg, 2kg, and 3kg, are placed at the vertices of an equilateral triangle of side 1m. Find the gravitational potential energy of this system.
Take G=6.67×10−11N−m2/kg2.
View SolutionThree particles each of mass m are kept at vertices of an equilateral triangle of side L. The gravitational field at centre due to these particle is
View SolutionThree masses of 1kg, 2kg, and 3kg, are placed at the vertices of an equilateral triangle of side 1m. Find the gravitational potential energy of this system.
Take G=6.67×10−11N−m2/kg2.
View SolutionThree point masses 'm' each are kept at three verties of a square pf side 'a' as shown in figure. Find gravitation potential and field strength at point O.
 .
.
View Solution
