Find the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x. Also find the potential at the centr of the square.
To find the potential energy of a system of four particles each of mass 2m kept at the vertices of a square of side x, and to find the potential at the center of the square, we can follow these steps:
Step 1: Understand the Configuration
We have four particles, each of mass 2m, placed at the vertices of a square. The side length of the square is x.
Step 2: Calculate the Distance Between Particles
The distance between any two adjacent particles (vertices) is simply the side of the square, which is x. The distance between two opposite vertices (diagonal) can be calculated using the Pythagorean theorem:
d=√x2+x2=√2x
Step 3: Calculate the Potential Energy
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
For our system, we need to consider the potential energy contributions from all pairs of particles.
1. Adjacent Pairs: There are 4 pairs of adjacent particles, each separated by a distance x:
Uadjacent=4(−G(2m)(2m)x)=−16Gm2x
2. Diagonal Pairs: There are 2 pairs of diagonal particles, each separated by a distance √2x:
Udiagonal=2(−G(2m)(2m)√2x)=−8Gm2√2x
3. Total Potential Energy:
Utotal=Uadjacent+Udiagonal=−16Gm2x−8Gm2√2x
Step 4: Simplify the Total Potential Energy
To combine these terms, we can factor out the common terms:
Utotal=−Gm2(16x+8√2x)
Calculating the second term:
8√2=4√2
Thus,
Utotal=−Gm2(16+4√2x)
Step 5: Calculate the Potential at the Center
To find the gravitational potential V at the center of the square, we consider the contribution from each mass. The distance from the center to any vertex is:
r=√22x
The potential at the center due to one mass is:
Vone=−G(2m)√22x=−4Gm√2x
Since there are four masses:
Vtotal=4(−4Gm√2x)=−16Gm√2x
Final Answers
1. The potential energy of the system is:
Utotal=−Gm2(16+4√2x)
2. The potential at the center of the square is:
Vtotal=−16Gm√2x
We have four particles, each of mass 2m, placed at the vertices of a square. The side length of the square is x.
The distance between any two adjacent particles (vertices) is simply the side of the square, which is x. The distance between two opposite vertices (diagonal) can be calculated using the Pythagorean theorem:
d=√x2+x2=√2x
The gravitational potential energy U between two masses m1 and m2 separated by a distance r is given by:
U=−Gm1m2r
For our system, we need to consider the potential energy contributions from all pairs of particles.
Uadjacent=4(−G(2m)(2m)x)=−16Gm2x
Udiagonal=2(−G(2m)(2m)√2x)=−8Gm2√2x
Utotal=Uadjacent+Udiagonal=−16Gm2x−8Gm2√2x
To combine these terms, we can factor out the common terms:
Utotal=−Gm2(16x+8√2x)
Calculating the second term:
8√2=4√2
Thus,
Utotal=−Gm2(16+4√2x)
To find the gravitational potential V at the center of the square, we consider the contribution from each mass. The distance from the center to any vertex is:
r=√22x
The potential at the center due to one mass is:
Vone=−G(2m)√22x=−4Gm√2x
Since there are four masses:
Vtotal=4(−4Gm√2x)=−16Gm√2x
1. The potential energy of the system is:
Utotal=−Gm2(16+4√2x)
Vtotal=−16Gm√2x
Topper's Solved these Questions
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - Try Yourself
33 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION -A (Objective Type Questions (one option is correct))
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
Similar Questions
Find the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
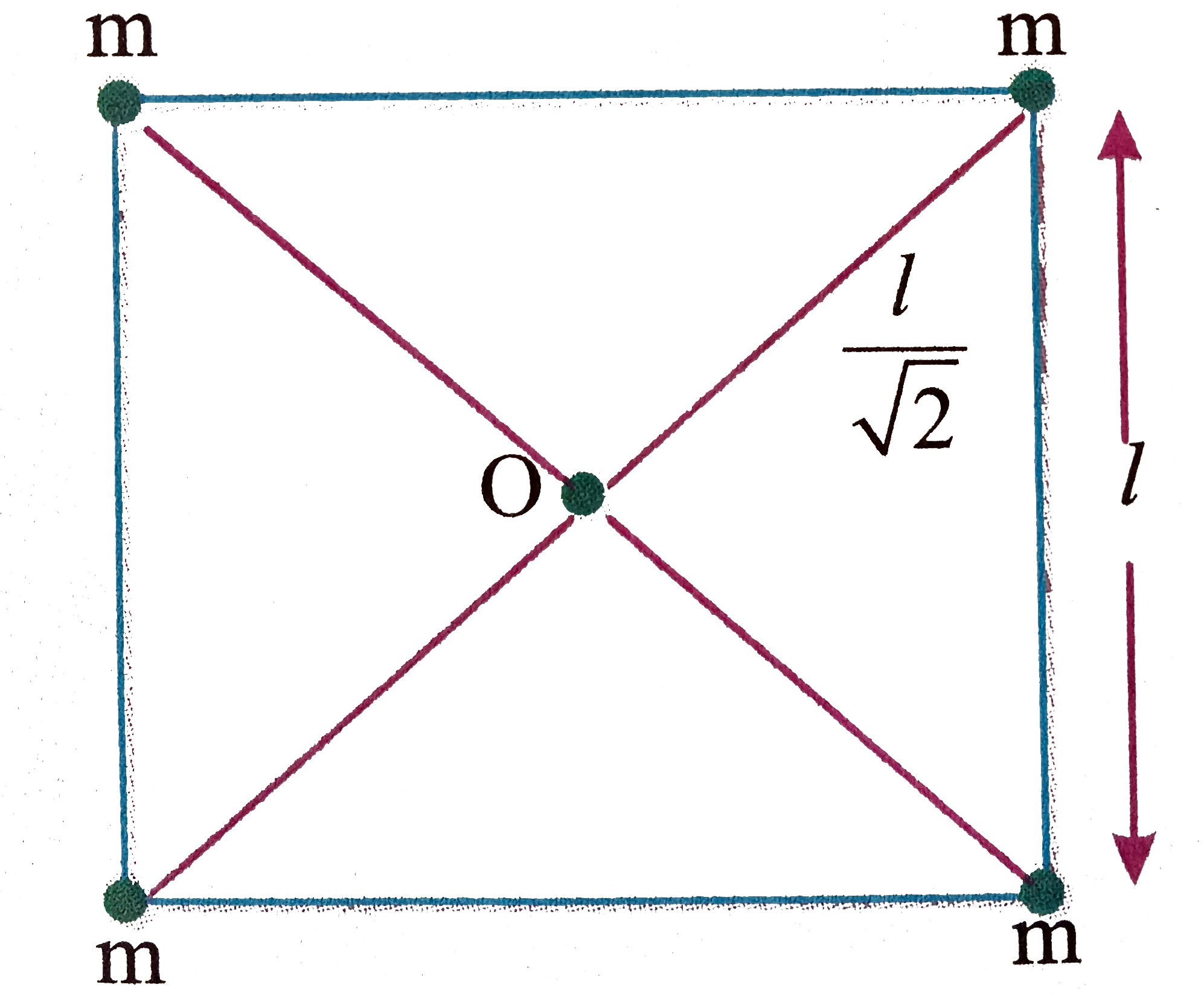
View SolutionFind the potential energy of a system of 3 particles kept at the vertices of an equilateral triangle of side r.
View Solution
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)
Find the potential energy of 4-particles, each of mass 1 kg placed at the four vertices of a square of side length 1 m.
View SolutionFour particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
View SolutionFind the electric potential energy of the system of charges
View SolutionFind the potential energy of a system of eight particles of mass M placed at the vertices of a cube of side L. neglect the self energy of the particles.
View SolutionFour point charges are placed at the corners of a square of side l. Calculate potential at the centre of square.

View SolutionThe gravitational potential energy of a system of three particles of mass m each kept at the vertices of equilateral triangle of side x will be
View SolutionFour particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
View Solution

