If M is the mass of the earth and R its radius, then ratio of the gravitational acceleration and the gravitational constant is
R2EME
MER2E
MER2E
MERE
The correct Answer is:B
(b) As g=GMER2E∴gG=MER2E
Topper's Solved these Questions
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Acceleration due to gravity below and above the surface of earth
8 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Gravitational Potential energy
7 Videos
- GRAVITATIONBOOK - NCERT FINGERTPS ENGLISHCHAPTER - GRAVITATIONEXERCISE - Universal law of Gravitations
14 Videos
- KINETIC THEORYBOOK - NCERT FINGERTPS ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assertion And Reason
10 Videos
Similar Questions
If M is the mass of the earth and R its radius, the radio of the gravitational acceleration and the gravitational constant is
View SolutionIf M be the mass of the earth, R its radius (assumed spherical) and G gravitational constant, then the amount of work that must be done on a body of mass m, so that it completely escapes from the gravity of the earth of the earth is given by
View SolutionThe acceleration due to gravity at a piece depends on the mass of the earth M, radius of the earth R and the gravitational constant G. Derive an expression for g?
View SolutionThe escape velocity of a body from the surface of the earth depends upon (i) the mass of the earth M, (ii) The radius of the eath R, and (iii) the gravitational constnat G. Show that v=k√GMR, using the dimensional analysis.
View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius R. Then the magnitude of gravitational force exerted by earth on the rod is

View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. If the magnitude of gravitational force exerted by earth on the rod is ηGMm12R2 then η is
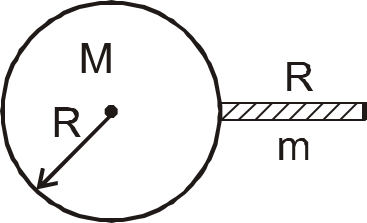
View SolutionA uniform thin rod of mass m and length R is placed normally on surface of earth as shown. The mass of earth is M and its radius is R. If the magnitude of gravitational force exerted by earth on the rod is ηGMm12R2 then η is

View SolutionThe ratio of gravitational mass to inertial mass is equal to:
View SolutionThe ratio of the inertial mass to gravitational mass is equal to
View SolutionIf the mass of moon is M81, where M is the mass of earth, find the distance of the point where gravitational field due to earth and moon cancel each other, from the centre of moon. Given the distance between centres of earth and moon is 60 R where R is the radius of earth
View Solution
