A parallel plate capacitor has plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has dielectric constant that varies as K(y)=k0(1+αy) where ‘y’ is the vertical distance measured from base of the plates. The total capacitance of the system is best given by: (K0 is constant)

A∈0K0d(1+α2l22)
A∈0K0d(1+αl)
A∈0K0d(1+2l24)
A∈0K0d(1+αl2)
The correct Answer is:D
All dC.s are in parallel
A= bl
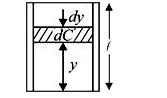
C=∫dC,dC=∈0bdyKd
∴C=∈0bK0dl∫0(1+αy)dy=∈0bK0ld(1+αl2)
C=A∈0K0d(1+αl2)
Similar Questions
A parallel plate capacitor has square plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as k(y)=K0(1+βy) where 'y' is the distance measured from bottom of capacitor. The total capacitance of the system is given by the expression:
View SolutionA parallel plate capacitor has plate area of A separated by distance between them. It is completely filled with dielectric medium, its dielectric constant increases linearly as move from one plate to other plate from k1 to k2 . Then the capacitance of system is given by :
View Solution
Knowledge Check
A parallel plate capacitor has plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as k(x)=K(1+ax) where ‘x’ is shown in figure. If (al)<<1 , the total capacitance of the system is best given by the expression:
 AAK∈0d(1+αl)BAk∈0d(1+αl2)CA∈0Kd(1+(αl2)2)DA∈0Kd(1+α2l22)
AAK∈0d(1+αl)BAk∈0d(1+αl2)CA∈0Kd(1+(αl2)2)DA∈0Kd(1+α2l22)A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
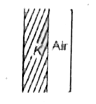 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
A parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionFigure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as K=K0+αx, where K and α are constants and x is the distance from the left end. Calculate the capacitance.

View SolutionA paralled plate capacitor is made of two square plates of side 'a' , separated by a distance d (dltlta). The lower triangular portion is filled with a dielecttic of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
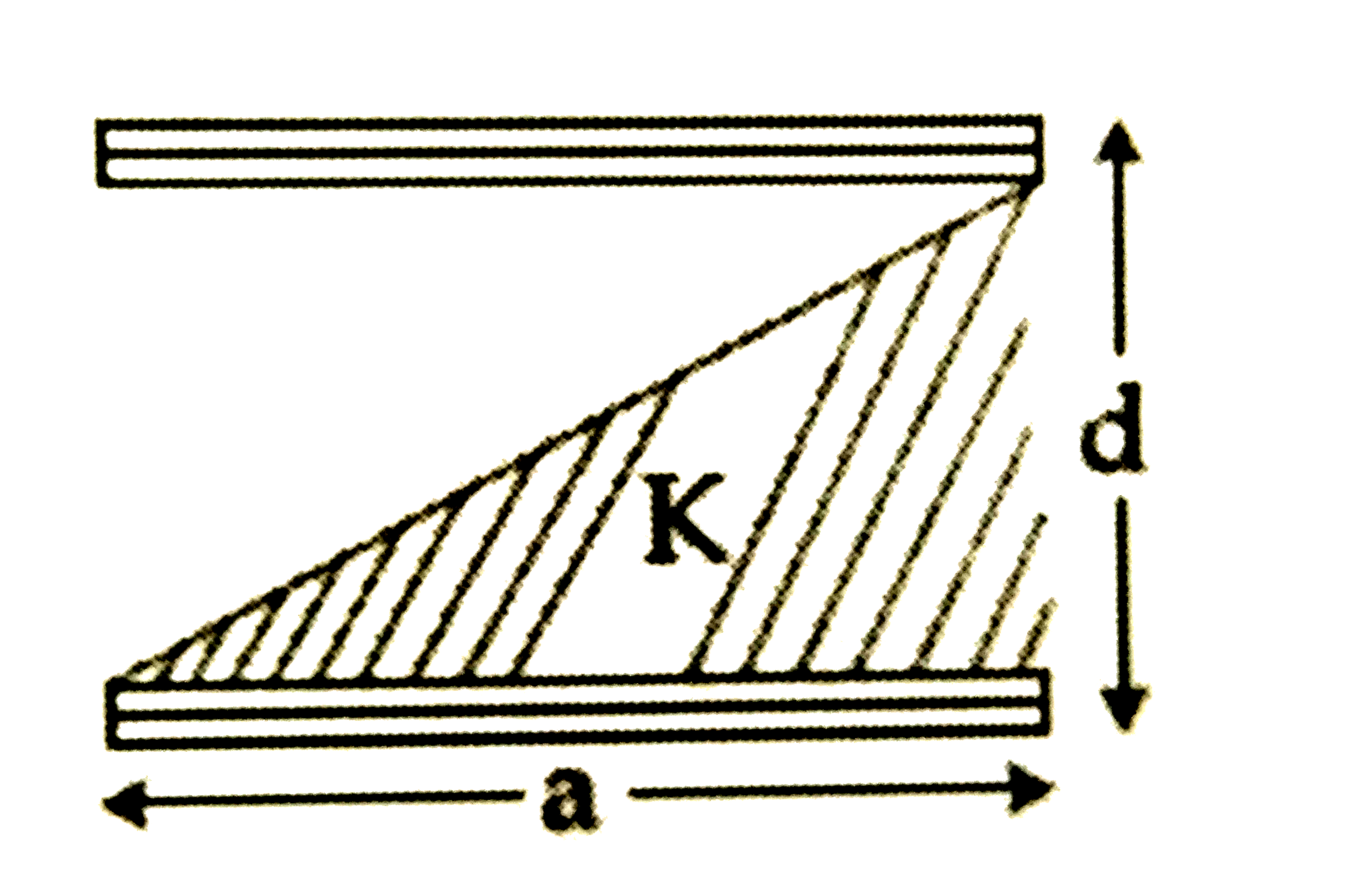
View SolutionA parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangement ?

View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View Solution
