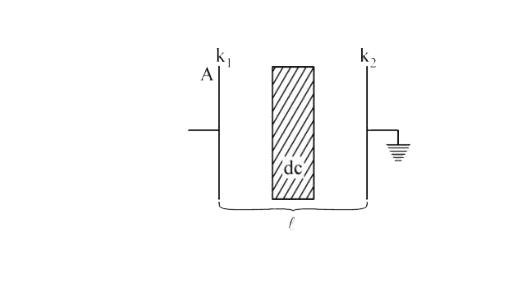
A parallel plate capacitor has plate area of A separated by distance between them. It is completely filled with dielectric medium, its dielectric constant increases linearly as move from one plate to other plate from $k_{1}$ to $k_{2}$ . Then the capacitance of system is given by :

A

$\frac{3 ε_{0} A (k_{2} - k_{1})}{l {log}_{e} (\frac{k_{2}}{k_{1}})}$

B

$\frac{2 ε_{0} A (k_{2} - k_{1})}{l {log}_{e} (\frac{k_{2}}{k_{1}})}$

C

$\frac{ε_{0} A (k_{2} - k_{1})}{l {log}_{e} (\frac{k_{2}}{k_{1}})}$

D

$\frac{ε_{0} A (k_{2} - k_{1})}{2 l {log}_{e} (\frac{k_{2}}{k_{1}})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

$d C = \frac{k ε_{0} A}{d x}$
$k = α x + β$
At x = 0, $k_{1} = β$
At x = l, $k_{2} = α l + β$
$k_{2} = α l + k_{1}$
$k_{2} - k_{1} = α l, α = \frac{k_{2} - k_{1}}{l}$
$k = k_{1} + (\frac{k_{2} - k_{1}}{l}) x$ , $d c = \frac{ε_{0} [(k_{1} + \frac{(k_{2} - k_{1})}{l}) x] 4}{d x}$
$\frac{1}{c} = \int \frac{1}{d C}$ , $\frac{1}{C} = \int_{0}^{l} \frac{d x}{ε_{0} [k_{1} + (\frac{k_{2} - k_{1}}{l}) x] 4}$
$C = \frac{ε_{0} A (k_{2} - k_{1})}{l {log}_{e} (\frac{k_{2}}{k_{1}})}$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Similar Questions

Knowledge Check

A parallel plate capacitor has plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as $k (x) = K (1 + a x)$ where ‘x’ is shown in figure. If $(a l) < < 1$ , the total capacitance of the system is best given by the expression:

A $\frac{A K \in_{0}}{d} {(1 + α l)}$
B $\frac{A k \in_{0}}{d} (1 + \frac{α l}{2})$
C $\frac{A \in_{0} K}{d} (1 + {(\frac{α l}{2})}^{2})$
D $\frac{A \in_{0} K}{d} (1 + \frac{α^{2} l^{2}}{2})$
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then

A $C = C [\frac{K}{K + 1}]$
B $C' = C [\frac{2 K}{K + 1}]$
C $C' = \frac{2 C}{K + 1}$
D $C' = C [1 + \frac{K}{2}]$
A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness $x < d$ with a dielectric constant K. Calculate the capacitance of the system.

A $\frac{2 K ε_{A}}{K d - x (K - 1)}$
B $\frac{K ε_{A}}{K 2 d - x (K - 1)}$
C $\frac{K ε_{A}}{K - x (K - 1)}$
D $\frac{K ε_{A}}{K d - x (K - 1)}$

Recommended Questions

Home
Ask Doubt
Profile