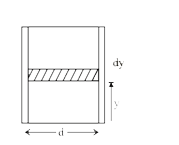
A parallel plate capacitor has square plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as k(y)=K0(1+βy) where 'y' is the distance measured from bottom of capacitor. The total capacitance of the system is given by the expression:

∈0AK0d(1+βA2)
∈0AK0d(√A+β√A2)
∈0AK0d(1+β√A2)
∈0√AK0d(√A+β√A2)
The correct Answer is:C
dC=∈0(√Ady)k(y)d,dC=(√A∈0K0)⎞⎟
⎟⎠(tay)dy)d
∴C=√A∈0K0dInt√A0(1+βy)dy
=√A∈0K0d(√A+βA2)⇒∈0AK0d(1+β√A2).
Similar Questions
A parallel plate capacitor has plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has dielectric constant that varies as K(y)=k0(1+αy) where ‘y’ is the vertical distance measured from base of the plates. The total capacitance of the system is best given by: (K0 is constant)

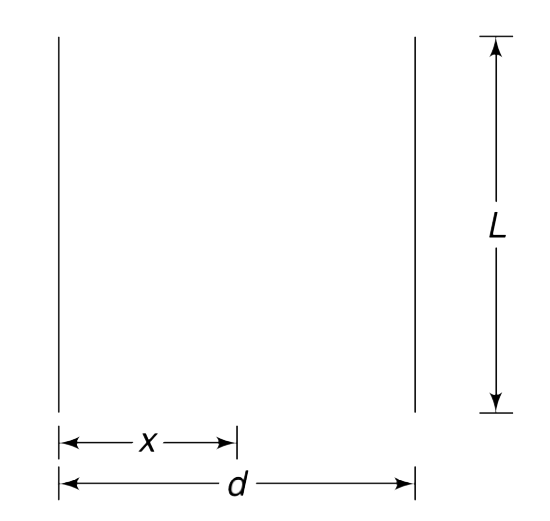
View SolutionA parallel plate capacitor has square plates of side length L kept at a separation d. The space between them is filled with a dielectric whose dielectric constant changes as K=eβx where x is distance measured from the left plate towards the right plate, and b is a positive constant. A poten- tial difference of V volt is applied with left plate positive.
(i) What happens to capacitance of the capacitor if d is increased ? What is the smallest possible capacitance that can be obtained by changing d ?
(ii) Write the expression of electric field between the plates as a function of x.
View Solution
Knowledge Check
A parallel plate capacitor has plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as k(x)=K(1+ax) where ‘x’ is shown in figure. If (al)<<1 , the total capacitance of the system is best given by the expression:
 AAK∈0d(1+αl)BAk∈0d(1+αl2)CA∈0Kd(1+(αl2)2)DA∈0Kd(1+α2l22)
AAK∈0d(1+αl)BAk∈0d(1+αl2)CA∈0Kd(1+(αl2)2)DA∈0Kd(1+α2l22)A parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.
 A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)
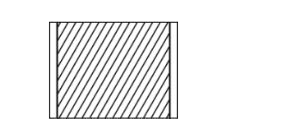
A2KεAKd−x(K−1)BKεAK2d−x(K−1)CKεAK−x(K−1)DKεAKd−x(K−1)A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
A parallel plate capacitor has plate area of A separated by distance between them. It is completely filled with dielectric medium, its dielectric constant increases linearly as move from one plate to other plate from k1 to k2 . Then the capacitance of system is given by :
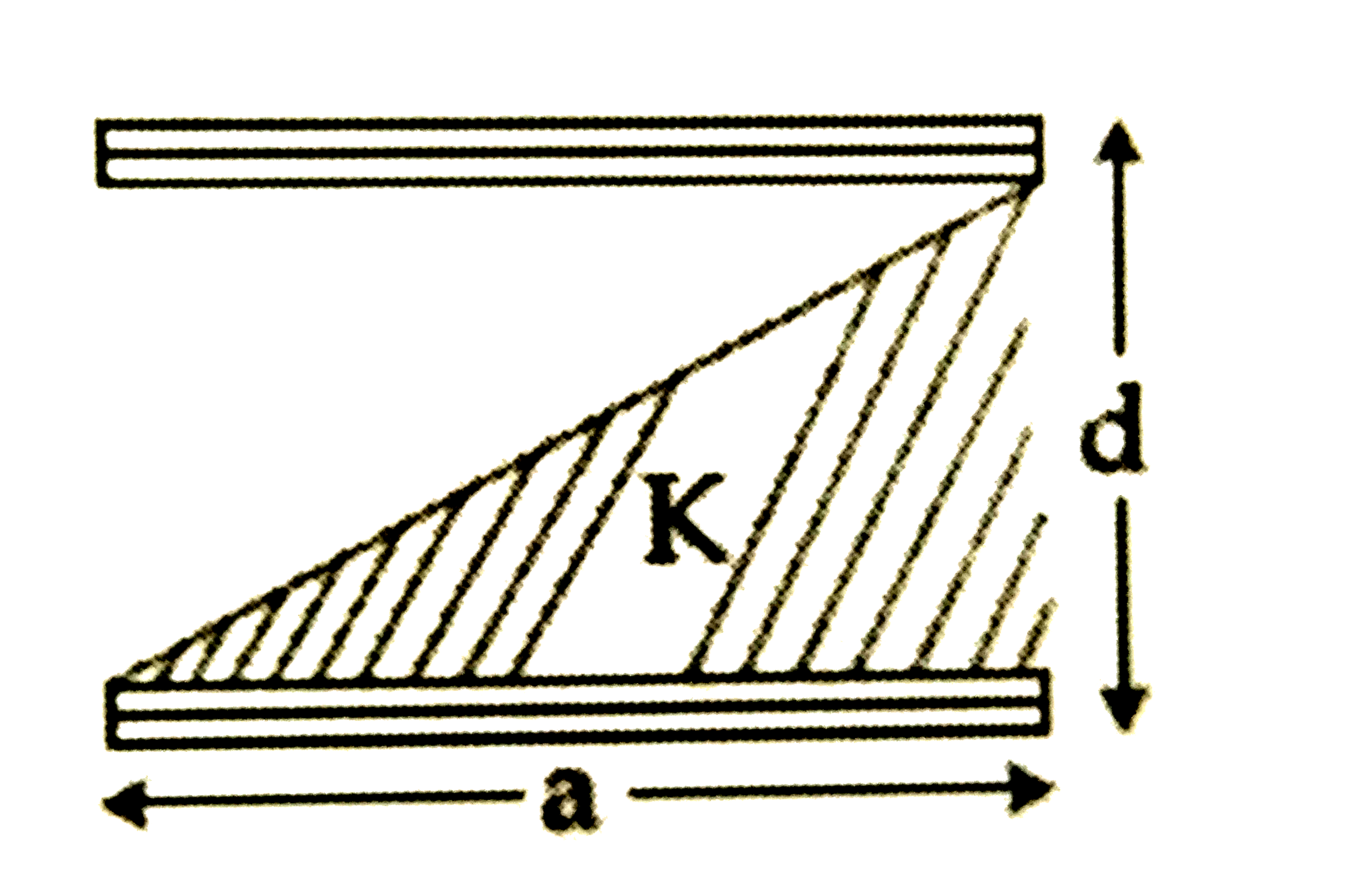
View SolutionA paralled plate capacitor is made of two square plates of side 'a' , separated by a distance d (dltlta). The lower triangular portion is filled with a dielecttic of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
View SolutionFigure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as K=K0+αx, where K and α are constants and x is the distance from the left end. Calculate the capacitance.

View SolutionA parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangement ?

View Solution

