A paralled plate capacitor is made of two square plates of side 'a' , separated by a distance d (dltlta). The lower triangular portion is filled with a dielecttic of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is :
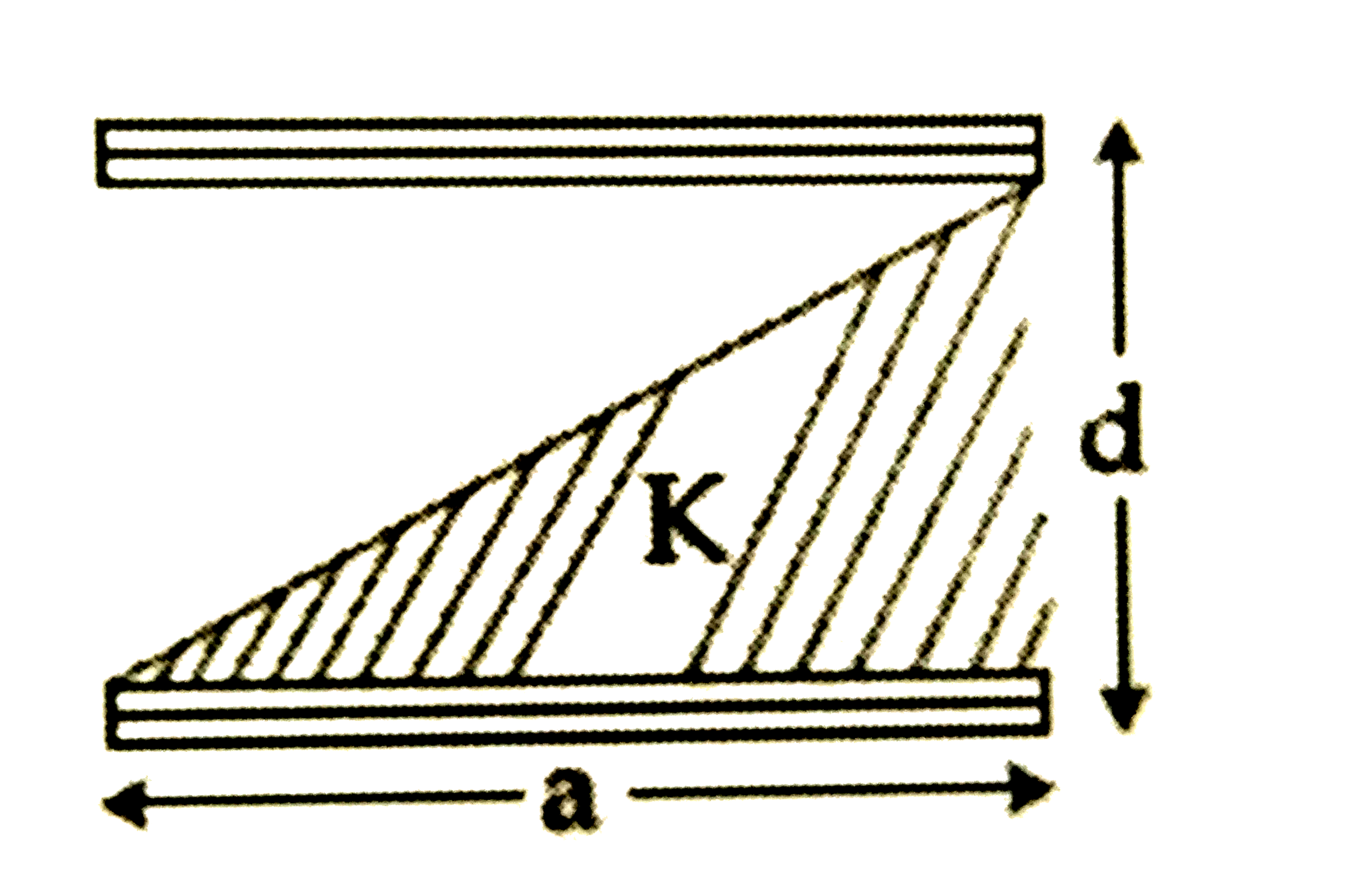
K∈0a22d(K+1)
K∈0a2d(K−1)InK
K∈0a2dInK
12K∈0a2d
Step by step video, text & image solution for A paralled plate capacitor is made of two square plates of side 'a' , separated by a distance d (dltlta). The lower triangular portion is filled with a dielecttic of dielectric constant K, as shown in the figure. Capacitance of this Capacitor is : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A parallel plate capacitor has square plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as k(y)=K0(1+βy) where 'y' is the distance measured from bottom of capacitor. The total capacitance of the system is given by the expression:

View SolutionFigure shown a parallel-plate capacitor having square plates of edge a and plate-separation d. The gap between the plates is filled with a dielectric of dielectric constant K which varies parallel to an edge as K=K0+αx, where K and α are constants and x is the distance from the left end. Calculate the capacitance.

View Solution
Knowledge Check
A parallel plate air capacitor has capacitance C. Half of space between the plates is filled with dielectric of dielectric constant K as shown in figure . The new capacitance is C . Then
 AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]
AC=C[KK+1]BC'=C[2KK+1]CC'=2CK+1DC'=C[1+K2]A paralle plate air capacitor has capacitance C. Now half of the space is fillel with a dielectric material with dielectric constant K as shown in figure . The new capacitance is C . Then
 AC'=C2[1+K]BC'=C[1+K]CC'=C[1+K2]DC'=C[12+K]
AC'=C2[1+K]BC'=C[1+K]CC'=C[1+K2]DC'=C[12+K]A parallel plate capacitor has plates of area A separated by distance ‘d’ between them. It is filled with a dielectric which has a dielectric constant that varies as k(x)=K(1+ax) where ‘x’ is shown in figure. If (al)<<1 , the total capacitance of the system is best given by the expression:
 AAK∈0d(1+αl)BAk∈0d(1+αl2)CA∈0Kd(1+(αl2)2)DA∈0Kd(1+α2l22)
AAK∈0d(1+αl)BAk∈0d(1+αl2)CA∈0Kd(1+(αl2)2)DA∈0Kd(1+α2l22)
Two parallel plate capacitors, each of capacitance 40 muF, are connected is series. The space between the plates of one capacitor is filled with a dielectric material of dielectric constant K =4. Find the equivalent capacitacne of the system.
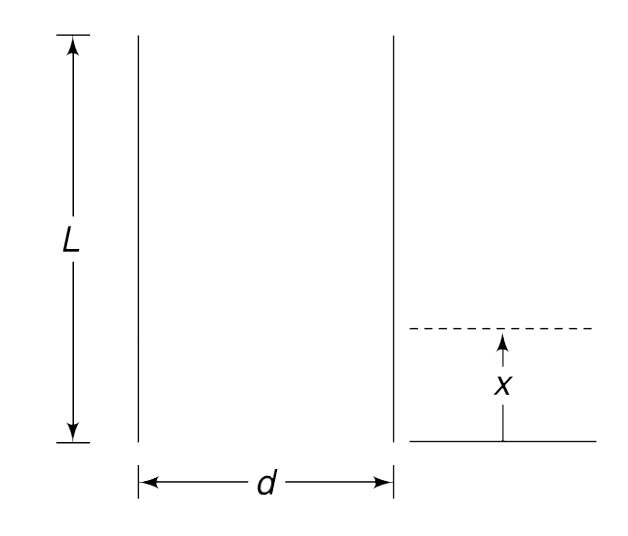
View SolutionA parallel plate capacitor has square plates of side length L. Plates are kept vertical at separation d between them. The space between the plates is filled with a dielectric whose dielectric constant (K) changes with height (x) from the lower edge of the plates as K=eβx where b is a positive constant. A potential difference of V is applied across the capacitor plates.
(i) Plot the variation of surface charge density (s) on the positive plate of the capacitor versus x.
(ii) Plot the variation of electric field between the plates as a function of x.
(iii) Calculate the capacitance of the capacitor.
View SolutionA parallel plate capacitor with air between the plates has a capacitance C. If the distance between the plates is doubled and the space between the plates is filled with a dielectric of dielectric constant 6, then the capacitance will become.
View SolutionConsider a disconnected. Plate capacitor of capacity 10μ with air filled in the gap between the plates. Now one-half of the space between the plates is filled with a dielectric of dielectric constant 4 as shown in .The capacity of the capacitor changes to
 .
.
View SolutionA capacitor of plate area A and separation d is filled with two dielectrics of dielectric constant K1=6andK2=4. New capacitance will be

View Solution
