Consider a pendulum consisting of a massless string with a mass at one end. The mass is held with the string horizontal and then released. The mass swings down, and on its way back up, the string is cut at point P when it makes an angle of with θ the vertical. Find the angle for θ which horizontal range .R. is maximum. Solution in Telugu
The speed at angle is given by conservation of energy.
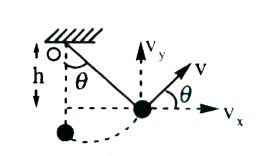
12mv2=mgh⇒12mv2=mglcosθ
v=√2glcosθ
When string is cut particle moves as a projectile with velocity component.
vx=vcosθvy=vsinθ
The time of flight is t=2(vyg)
Range is, R=vxt=vx(2vyg)
=2vxvyg=2(vcosθ)(vsinθ)g=2v2sinθcosθg
=2(2glcosθ)sinθcosθg=4lcos2θsinθ
Differentiating .R. with respect to .θ. and equating it to zero we get
0=4l(−2cosθsinθ)sinθ+cos2θcosθ
or, 2sin2θcosθ=cos3θ, or tanθ=1/√2
Topper's Solved these Questions
- WORK POWER ENERGYBook:AAKASH SERIESChapter:WORK POWER ENERGYExercise:EXERCISE - 1A
Explore 117 Videos
- WORK POWER ENERGYBook:AAKASH SERIESChapter:WORK POWER ENERGYExercise:EXERCISE - 1B
Explore 39 Videos
- WORK -POWER-ENERGYBook:AAKASH SERIESChapter:WORK -POWER-ENERGYExercise:PRACTICE SHEET (ADVANCED) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
Explore 36 Videos
- WORK, POWER & ENERGY Book:AAKASH SERIESChapter:WORK, POWER & ENERGY Exercise:PRACTICE EXERCISE (PERFECTLY INELASTIC COLLISIONS)
Explore 5 Videos
Similar Questions
If l1,m1,n1 and l2,m2,n2 are the direction cosines of two vectors and θ is the angle between them, then the value of cos θ is
View Solution(A): A spring has potential energy, both when it is compressed or stretched.
(R) : In compressing or stretching, work is done on the spring against the restoring force.
View SolutionThe velocity of a particle of mass 10−2kg is given as →v=(2xˆu+3yˆj+4zˆk) m/sec (where x, y and z are in meter). The amount of work done by applied force in displacing a particle from (1m, 2m, 0) to (-1m, 3m, 1m) is …..
View SolutionA shot moving with a velocity 140ms−1 collides a wooden block and comes to rest in it. If mass of the block is 13 times the mass of the shot, velocity of the block is
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle theta with the vertical. The angle theta is equal to
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionA simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle alpha . A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle theta which the string makes with the vertical after hitting the pin is
View SolutionA particle of mass m suspended by a string of length l revolves in a horizontal circle (θ is the angle the string makes with vertical). Which of the following statement(s) is // are correct?
View SolutionFigure below shows a small mass connected to a string, which is attached to a vertical post. If the ball is released when the string is horizontal as shown, the magnitude of the total acceleration (including radial and tangential) of the mass as a function of the angle Theta is
View SolutionA simple pendulum is released from rest at the horizontally stretched position. When the string makes an angle theta with the vertical, the angle theta which the acceleration vector of the bob makes with the string is given by–
View SolutionA pendulum bob of mass m and length L is released from angle theta with the vertical. Find (a) the speed of the bob at the bottom of the swing and (b) tension in the string at that time
View SolutionIf a simple pendulum of mass m is released from a horizontal position, find the tension in the string as a function of the angle θ with the horizontal.
View SolutionA pendulum consists of a small mass m at the end of a string of length L. The pendulum is pulled aside making an angle theta with the vertical and released. Taking the suspension point as the axis, at the instant of release
View SolutionMass of the bob of a pendulum is 100g and the length of the string is 1m . The bob is initially held is such a way that the string is horizontal . The bob is then released. Find the kinetic energy of the bob when the string makes an angle of (i) 0^@ with vertical
View SolutionMass of the bob of a pendulum is 100g and the length of the string is 1m . The bob is initially held is such a way that the string is horizontal . The bob is then released. Find the kinetic energy of the bob when the string makes an angle of (ii) 30^@ with the vertical .
View Solution