At low pressure, the van der Waal's equation become :
(a)PVm=RT
(b)P(Vm−b)=RT
(c)(P+aV2M)Vm=RT
(d)P=RTVm+aV2m
PVm=RT
P(Vm−b)=RT
(P+aV2M)Vm=RT
P=RTVm+aV2m
The correct Answer is:c
To solve the question regarding the van der Waals equation at low pressure, we will follow these steps:
Step 1: Write down the van der Waals equation
The van der Waals equation is given by:
P+aV2m(Vm−b)=RT
where:
- P = pressure
- Vm = molar volume
- a = measure of the attractive forces between particles
- b = volume occupied by the particles themselves
- R = universal gas constant
- T = temperature
Step 2: Consider the conditions at low pressure
At low pressure, the volume of the gas is large, which means that the excluded volume b becomes negligible. Thus, we can simplify the equation by ignoring the term b.
Step 3: Simplify the equation
Neglecting b, the equation simplifies to:
P+aV2mVm=RT
This can be rearranged to:
P+aVm=RT
Step 4: Rearranging to isolate P
To isolate P, we can rearrange the equation:
P=RT−aVm
Step 5: Identify the correct option
Now, let's analyze the options provided:
- (a) PVm=RT
- (b) P(Vm−b)=RT
- (c) (P+aV2m)Vm=RT
- (d) P=RTVm+aV2m
From our simplification, we see that option (c) matches our derived equation at low pressure.
Final Answer
The correct answer is:
(c) (P+aV2m)Vm=RT
---
The van der Waals equation is given by:
P+aV2m(Vm−b)=RT
where:
- P = pressure
- Vm = molar volume
- a = measure of the attractive forces between particles
- b = volume occupied by the particles themselves
- R = universal gas constant
- T = temperature
At low pressure, the volume of the gas is large, which means that the excluded volume b becomes negligible. Thus, we can simplify the equation by ignoring the term b.
Neglecting b, the equation simplifies to:
P+aV2mVm=RT
This can be rearranged to:
P+aVm=RT
To isolate P, we can rearrange the equation:
P=RT−aVm
Now, let's analyze the options provided:
- (a) PVm=RT
- (b) P(Vm−b)=RT
- (c) (P+aV2m)Vm=RT
- (d) P=RTVm+aV2m
The correct answer is:
(c) (P+aV2m)Vm=RT
Topper's Solved these Questions
- GASEOUS STATEBook:NARENDRA AWASTHI ENGLISHChapter:GASEOUS STATEExercise:Level 2
Explore 30 Videos
- GASEOUS STATEBook:NARENDRA AWASTHI ENGLISHChapter:GASEOUS STATEExercise:Level 3 Passage 1
Explore 4 Videos
- ELECTROCHEMISTRYBook:NARENDRA AWASTHI ENGLISHChapter:ELECTROCHEMISTRYExercise:Subjective problems
Explore 14 Videos
- IONIC EEQUILIBRIUMBook:NARENDRA AWASTHI ENGLISHChapter:IONIC EEQUILIBRIUMExercise:Subjective problems
Explore 1 Video
Similar Questions
Knowledge Check
The van der Waal equation of gas is
(P+n2aV2)(V−nb)=nRTA(i) CO2 , (ii) H2B(i) CH4 , (ii) CO2C(i) H2 , (ii) CO2DO2, (ii) H2In the Van der Waals equation (P+aV2)(V−b) = constant, the unit of a is
Adyne/cm5Bdyne/cm4Cdyne/cm3Ddyne/cm2
At low pressure the van der Waals' equation is reduced to [P+aV2]V=RT The compressibility factor can be given as .
View SolutionUse of dilution formula (M1V1=M2V2)

View SolutionAt low pressure, if RT=2√a.p, then the volume occupied by a real gas is :
(a)2RTP
(b)2PRT
(c)RT2P
(d)2RTP
View SolutionThe van der Waals' equation for one mole may be expressed as
V3M−(b+RTP)V2m+aVmP−abP=0
where Vm is the molar volume of the gas. Which of the followning is incorrect?
View SolutionThe equation of PcVcRTc = ..........
View SolutionAt a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
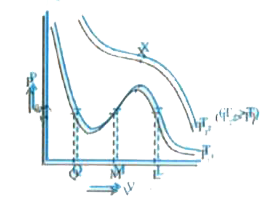
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given as
View Solution