The van der Waals' equation for one mole may be expressed as
V3M−(b+RTP)V2m+aVmP−abP=0
where Vm is the molar volume of the gas. Which of the followning is incorrect?
For a temperature less than TC,V has three real roots
For a temperature less than TC,V has three imaginary roots
For a temperature equal to TC all three roots of V are real and identical
On increasing the temp. (T<TC), the three roots become closer to one another
The correct Answer is:b
To solve the question regarding the van der Waals equation for one mole, we need to analyze the equation and the properties of its roots under different conditions. The van der Waals equation is given as:
V3m−(b+RTP)V2m+aVmP−abP=0
where:
- Vm is the molar volume of the gas,
- R is the universal gas constant,
- T is the temperature,
- P is the pressure,
- a and b are van der Waals constants specific to the gas.
1. Understand the Roots of the Equation:
The cubic equation can have three roots (real or imaginary) depending on the values of T, P, a, and b. The nature of the roots changes with temperature.
2. Critical Temperature Condition:
At the critical temperature Tc, the behavior of the roots changes. It is known that at T<Tc, the equation can yield one real root and two imaginary roots. This is a crucial point in understanding the behavior of gases under different conditions.
3. Analyze the Statements:
The question asks to identify which statement regarding the roots of the equation is incorrect. We need to evaluate the statements related to the number of real and imaginary roots at different temperatures.
4. Evaluate the Statements:
- Statement 1: At T<Tc, there is one real root and two imaginary roots. This is true.
- Statement 2: At T=Tc, all roots are real and equal. This is also true.
- Statement 3: At T>Tc, all roots are real. This is true.
- Statement 4: The statement claiming that at T<Tc all roots are real is incorrect.
5. Conclusion:
The incorrect statement is the one that suggests all roots are real at temperatures below the critical temperature Tc.
Final Answer:
The incorrect statement is that at T<Tc, all roots of the van der Waals equation are real.
- Vm is the molar volume of the gas,
- R is the universal gas constant,
- T is the temperature,
- P is the pressure,
- a and b are van der Waals constants specific to the gas.
The cubic equation can have three roots (real or imaginary) depending on the values of T, P, a, and b. The nature of the roots changes with temperature.
At the critical temperature Tc, the behavior of the roots changes. It is known that at T<Tc, the equation can yield one real root and two imaginary roots. This is a crucial point in understanding the behavior of gases under different conditions.
The question asks to identify which statement regarding the roots of the equation is incorrect. We need to evaluate the statements related to the number of real and imaginary roots at different temperatures.
- Statement 1: At T<Tc, there is one real root and two imaginary roots. This is true.
- Statement 2: At T=Tc, all roots are real and equal. This is also true.
- Statement 3: At T>Tc, all roots are real. This is true.
- Statement 4: The statement claiming that at T<Tc all roots are real is incorrect.
The incorrect statement is the one that suggests all roots are real at temperatures below the critical temperature Tc.
The incorrect statement is that at T<Tc, all roots of the van der Waals equation are real.
Topper's Solved these Questions
- GASEOUS STATEBook:NARENDRA AWASTHI ENGLISHChapter:GASEOUS STATEExercise:Level 2
Explore 30 Videos
- GASEOUS STATEBook:NARENDRA AWASTHI ENGLISHChapter:GASEOUS STATEExercise:Level 3 Passage 1
Explore 4 Videos
- ELECTROCHEMISTRYBook:NARENDRA AWASTHI ENGLISHChapter:ELECTROCHEMISTRYExercise:Subjective problems
Explore 14 Videos
- IONIC EEQUILIBRIUMBook:NARENDRA AWASTHI ENGLISHChapter:IONIC EEQUILIBRIUMExercise:Subjective problems
Explore 1 Video
Similar Questions
The van der Waal's equation of state for some gases can be expressed as :
(P+aV2)(V−b)=RT
Where P is the pressure , V is the molar volume , and T is the absolute temperature of the given sample of gas and a,b,andR are constants.
Which of the following does not have the same dimensional formula as that for RT?
View SolutionThe van der Waal's equation of state for some gases can be expressed as :
(P+aV2)(V−b)=RT
Where P is the pressure , V is the molar volume , and T is the absolute temperature of the given sample of gas and a,b,andR are constants.
In the above problem , the dimensional formula for RT is same as that of
View Solution
Knowledge Check
The van der Waal equation of gas is
(P+n2aV2)(V−nb)=nRTA(i) CO2 , (ii) H2B(i) CH4 , (ii) CO2C(i) H2 , (ii) CO2DO2, (ii) H2
The van der Waal's equation of state for some gases can be expressed as :
(P+aV2)(V−b)=RT
Where P is the pressure , V is the molar volume , and T is the absolute temperature of the given sample of gas and a,b,andR are constants.
The dimensions of a are
View SolutionThe van der Waal equation of gas is
(P+n2aV2)(V−nb)=nRT
View SolutionAt a particular temperature and pressure for a real gas Van der Waal's equation can be written as:
(P+aV2m)(Vm−b)=RT
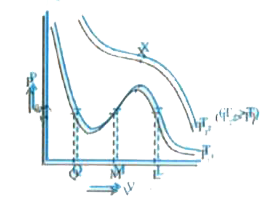
where Vm is molar volume of gas. This is cubic equation in the variable Vm and therefore for any single value of P & T there should be 3 values of Vm. Which are shown in graph as Q, M and L.
As temperature is made to increase at a certain higher temperature the three values of Vm becomes identical. The temperature, pressure & molar volume at point X are called Tc, Pc & Vc for real gas. The compressibility factor in terms of Pc, Vc and T is called Zc.
The expression of Van dcr Waal's constant 'a' can be given as
View SolutionA graph is plotted between PVm along y-axis and P along x-axis, where Vm is the molar volume of a real gas. Find the intercept .
View SolutionThe Van der waal's equation for n moles of a real gas is given by (P+n2aV2)(V−nb)=nRT, where
P pressure of gas, V= volume of gas, T= temperature of gas
R= molar gas constant, a & b= Van der waal's constant
Which of the following have the same dimensions as those of nRT.
View SolutionOne of the important approach to the study of real gases involves the analysis of parameter Z called the compressibility factor Z=PVmRT where P is pressure, Vm is molar volume, T is absolute temperature and R is the universal gas constant. such a relation can also be expressed as Z=(VmrealVmal) (where Vmal and Vmreal are the molar volume for ideal and real gas respectively). Gas corresponding Z<1 have attractive forces amoung constituent particles. As the pressure is lowered or temperature is increased the value of Z approaches 1. (reaching the ideal behaviour)
For a real gas GZ>1 at STP Then for 'G': Which of the following is true:
View SolutionA graph is plotted between PVm along Y-axis and P along X-axis whre Vm is the molar volume of a real gas Find the intercept along Y-axis .
View Solution

