A sample of an ideal gas is expanded 1m3 to 3m3 in a reversible process for which P=KV2 , with K=6bar/m6. What is work done by the gas (in kJ) ?
5200 KJ
15600 kJ
52 kJ
5267 .6 kJ
The correct Answer is:A
To solve the problem of calculating the work done by an ideal gas during a reversible expansion from 1m3 to 3m3 with the pressure given by P=KV2 (where K=6bar/m6), we can follow these steps:
1. Identify the Work Done Formula:
The work done W by the gas during an expansion is given by the integral:
W=∫V2V1PdV
where V1 is the initial volume and V2 is the final volume.
2. Substitute the Pressure Equation:
Given that P=KV2, we can substitute this into the work formula:
W=∫31KV2dV
3. Factor Out the Constant:
Since K is a constant, it can be factored out of the integral:
W=K∫31V2dV
4. Integrate V2:
The integral of V2 is:
∫V2dV=V33
Therefore, we evaluate this from 1 to 3:
W=K(V33)31=K(333−133)
5. Calculate the Values:
Now calculate the values:
W=K(273−13)=K(9−13)=K(27−13)=K(263)
6. Substitute the Value of K:
Substitute K=6bar/m6:
W=6(263)=1563=52bar⋅m3
7. Convert to Kilojoules:
Since 1bar⋅m3=100kJ:
W=52bar⋅m3×100kJ/bar=5200kJ
Final Answer:
The work done by the gas is 5200kJ.
The work done W by the gas during an expansion is given by the integral:
W=∫V2V1PdV
where V1 is the initial volume and V2 is the final volume.
Given that P=KV2, we can substitute this into the work formula:
W=∫31KV2dV
Since K is a constant, it can be factored out of the integral:
W=K∫31V2dV
The integral of V2 is:
∫V2dV=V33
Therefore, we evaluate this from 1 to 3:
W=K(V33)31=K(333−133)
Now calculate the values:
W=K(273−13)=K(9−13)=K(27−13)=K(263)
Substitute K=6bar/m6:
W=6(263)=1563=52bar⋅m3
Since 1bar⋅m3=100kJ:
W=52bar⋅m3×100kJ/bar=5200kJ
The work done by the gas is 5200kJ.
Topper's Solved these Questions
- THERMODYNAMICSBook:NARENDRA AWASTHI ENGLISHChapter:THERMODYNAMICSExercise:Level 2
Explore 40 Videos
- THERMODYNAMICSBook:NARENDRA AWASTHI ENGLISHChapter:THERMODYNAMICSExercise:Level 3
Explore 89 Videos
- STOICHIOMETRYBook:NARENDRA AWASTHI ENGLISHChapter:STOICHIOMETRYExercise:Match the Colum-II
Explore 6 Videos
Similar Questions
A sample of an ideal gas is expanded from 1dm3 to 3 in a reversible process for which P=KV3, with K=1/5(atm/dm3), what is work done by gas (Latm)
View SolutionA sample of an ideal gas is expanded to twice its original volume of 1m3 in a reversible process for which P=αV2, where α=5atmm−6. If CV,m=20Jmol−1K−1, determine moalr change in entropy (ΔSm) for the process.
View SolutionA sample of ideal gas is expanded to twice its original volume of 1.00m3 in a quasi-static process for which p=αV2, with α=5.00atm/m6, as shown in Fig. How much work is done by the expanding gas?
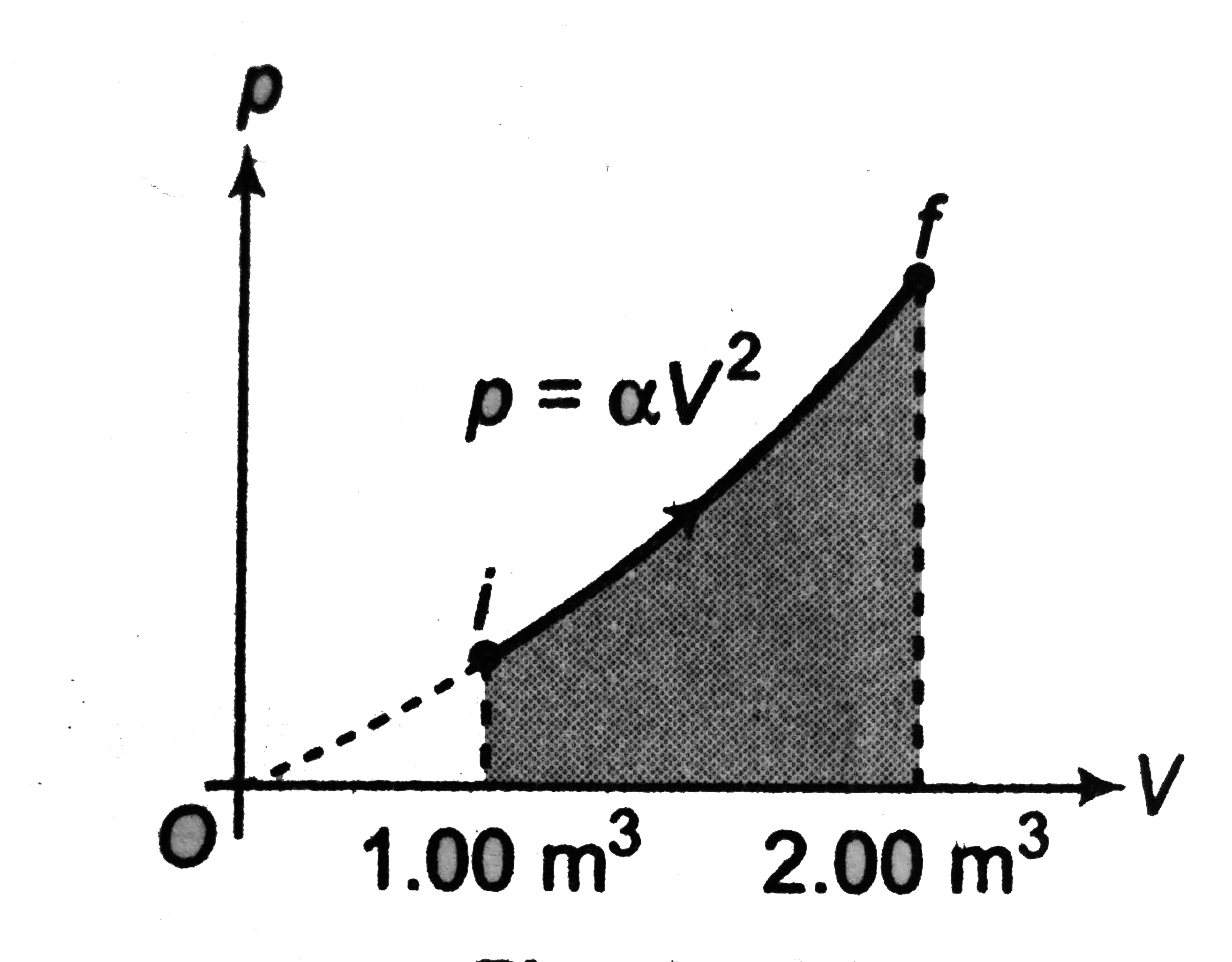
View SolutionA sample of ideal gas is expanded to twice its original volume of 1.00m3 in a quasi-static process for which p=αV2, with α=5.00atm/m6, as shown in Fig. How much work is done by the expanding gas?

View Solution1 moles of an ideal gas expanded spontaneously into vaccum. The work done will be
View Solution2 mole of an ideal monoatomic gas undergoes a reversible process for which PV2=C. The gas is expanded from initial volume of 1 L to final volume of 3 L starting from initial temperature of 300 K. Find ΔH for the process :
View SolutionIn figure, a sample of 3 moles of an ideal gas is undergoing through a cyclic process ABCA.A total of 1500J of heat is withdraw from the sample in the process. The work done by the gas during the part BC is −PKJ.FINDP.(R=253J/moleK)

View SolutionAn ideal gas expands from 10−3m3 to 10−2m3 at 300 K against a constant pressure of 105Nm−2. The workdone is
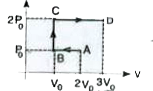
View SolutionP-V diagram of an ideal gas is as shown in figure. Work done by the gas in the process ABCD is
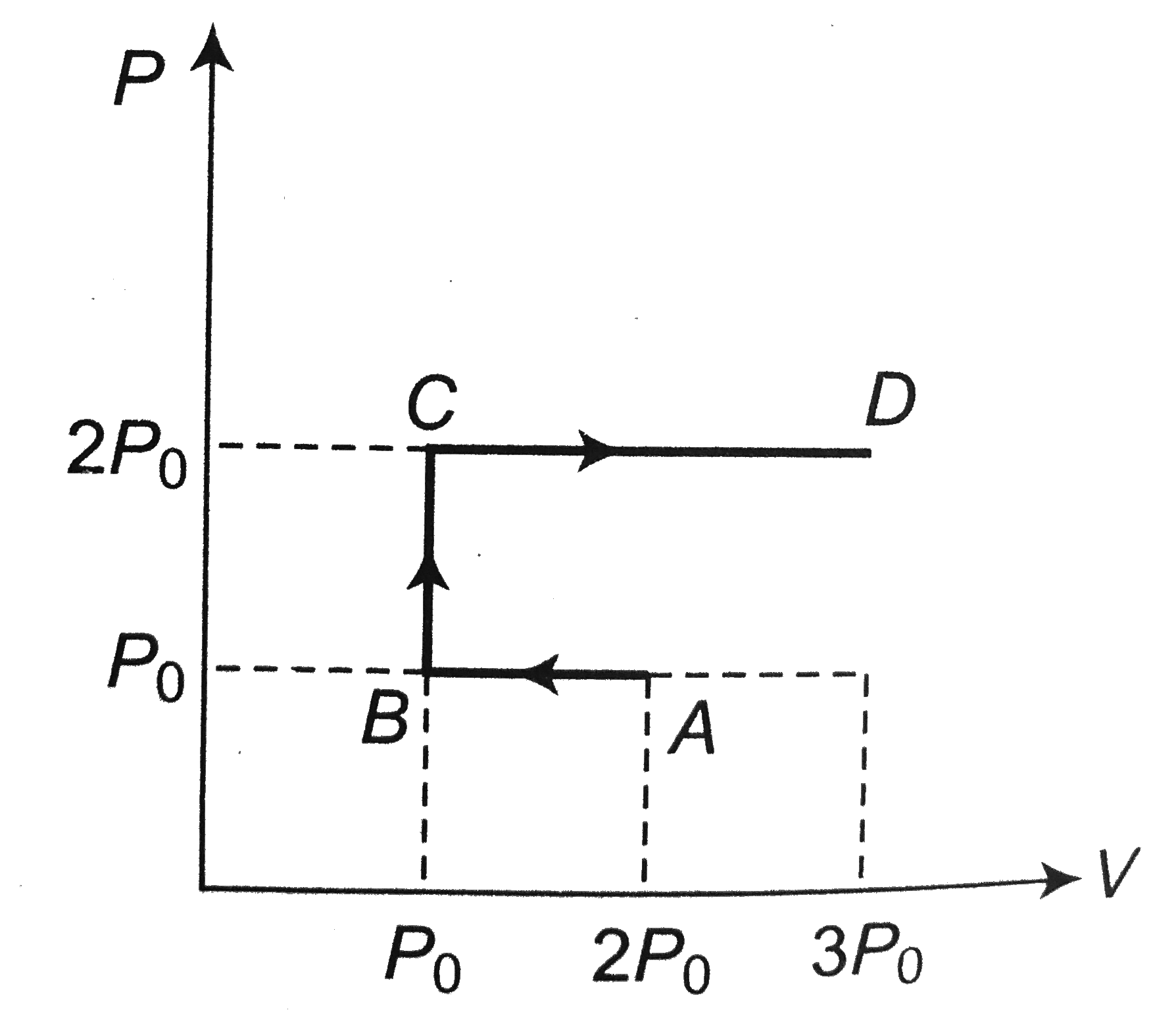
View SolutionP−V diagram of an ideal gas is as shown in figure. Work done by the gas in process ABCD is
View Solution