A sphere of radius 1.00 cm is placed in the path of a parallel beam of light of large aperture. The intensity of the light is 0.50 W cm−2. If the sphere completely absorbs the radiation falling on it, find the force exerted by the light beam on the sphere.
To find the force exerted by the light beam on the sphere, we can use the relationship between intensity, area, and force. Here’s a step-by-step solution:
Step 1: Understand the Given Data
- Radius of the sphere, r=1.00cm=0.01m
- Intensity of the light, I=0.50W/cm2=50W/m2 (since 1cm2=10−4m2)
Step 2: Calculate the Area of the Sphere
The area A of the sphere that is exposed to the light can be calculated using the formula for the surface area of a sphere:
A=4πr2
Substituting the radius:
A=4π(0.01)2=4π(0.0001)=0.0004πm2
Step 3: Calculate the Power Absorbed by the Sphere
The power P absorbed by the sphere can be calculated using the intensity and the area:
P=I⋅A
Substituting the values of intensity and area:
P=50W/m2⋅0.0004πm2=0.02πW
Step 4: Calculate the Force Exerted by the Light Beam
When the sphere completely absorbs the radiation, the force F exerted by the light beam can be calculated using the formula:
F=Pc
where c is the speed of light, approximately 3×108m/s.
Substituting the values:
F=0.02π3×108
Calculating this gives:
F≈0.062833×108≈2.094×10−10N
Step 5: Final Calculation
To express the force in a more standard form, we can round it:
F≈2.1×10−10N
Conclusion
The force exerted by the light beam on the sphere is approximately:
F≈2.1×10−10N
---
- Radius of the sphere, r=1.00cm=0.01m
- Intensity of the light, I=0.50W/cm2=50W/m2 (since 1cm2=10−4m2)
The area A of the sphere that is exposed to the light can be calculated using the formula for the surface area of a sphere:
A=4πr2
Substituting the radius:
A=4π(0.01)2=4π(0.0001)=0.0004πm2
The power P absorbed by the sphere can be calculated using the intensity and the area:
P=I⋅A
Substituting the values of intensity and area:
P=50W/m2⋅0.0004πm2=0.02πW
When the sphere completely absorbs the radiation, the force F exerted by the light beam can be calculated using the formula:
F=Pc
where c is the speed of light, approximately 3×108m/s.
F=0.02π3×108
Calculating this gives:
F≈0.062833×108≈2.094×10−10N
To express the force in a more standard form, we can round it:
F≈2.1×10−10N
The force exerted by the light beam on the sphere is approximately:
F≈2.1×10−10N
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer
13 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - objective II
7 Videos
- PERMANENT MAGNETSBOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Short Answer
11 Videos
- PHOTOMETRYBOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions
38 Videos
Similar Questions
A perfectly reflecting solid hemisphere of radius R is placed in the path of a parallel beam of light of large aperture. If the beam carrries an intensity l, find the force exerted by the beam on the hemisphere.
View SolutionA concave lens is placed in the path of a uniform parallel of beam of light falling on a screen as shown . Then
_E01_089_Q01.png)
View SolutionIn the path of a uniform light beam of large cross-sectional area and intensity I. a solid sphere of redius R which is perfectly reflecting is placed . Find the force exerted on this sphere due to the light beam.
View SolutionFind the amplitude of the electric field in a parallel bean of light of intensity 2.0Wm−2.
View SolutionA parallel beam of light falls on a solid tranparent sphere.
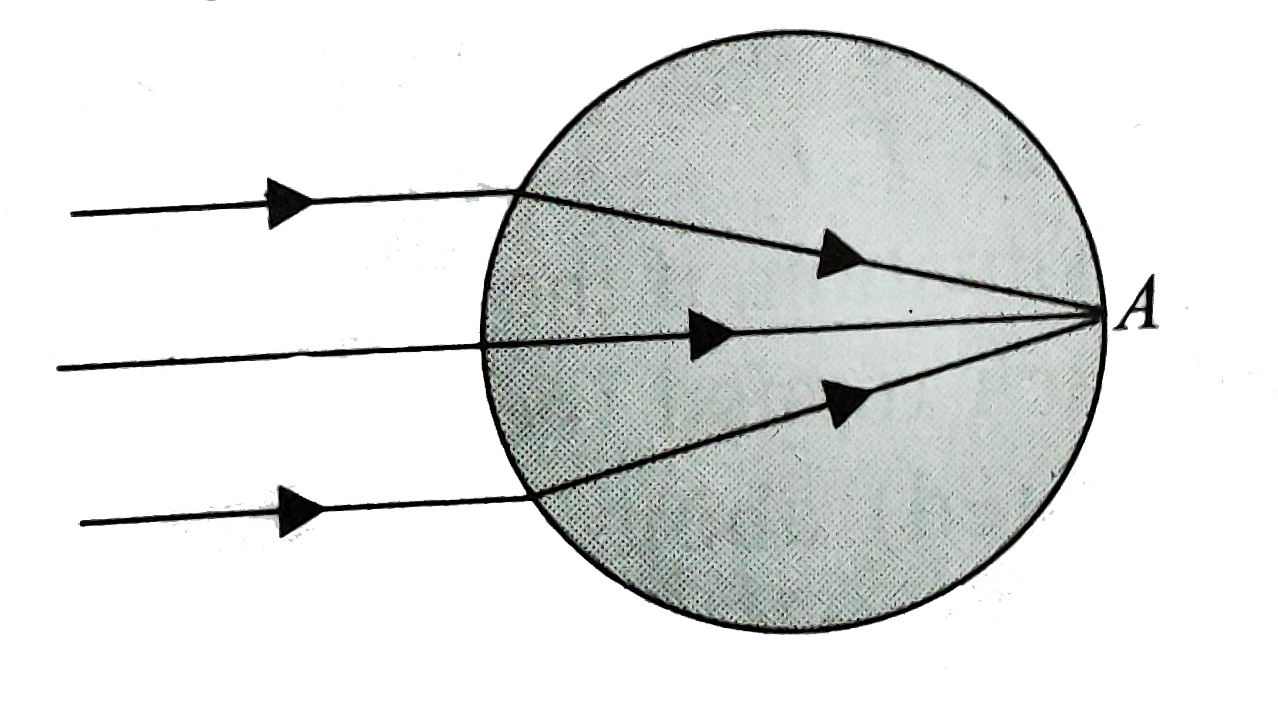
Q. Which is corret?
View SolutionA parallel beam of monochromatic light of wavelength 500nm is incident normally on a perfectly absorbing surface. The power through any cross- section of the beam is 10 W. Find (a) the number of photons absorbed per second by the surface and (b) the force exerted by the light beam on the surface.
View SolutionA parellel beam of monochromatic light of wavelength 500 nm is incident normally on a perfectly absorbing surface. The power through any cross section of the beam is 10 W. Find
(a) the number of photons absorbed per second by the surface and
(b) the force exerted by the light beam on the surface.
View SolutionFind the amplitude of electric and magnetic fields in parallel beam of light of intensity 4.0Wm−2
View SolutionA convex lens of diameter 8.0 cm is used to focus a parallel beam of light of wavelength 620 nm. If the light be focused at a distance of 20 cm from the lens, what would be the radius of the central bright spot formed ?
View SolutionA 100 W light bulb is placed at the centre of a spherical chamber of radius 20cm. Assume that 60% of the energy supplied to the bulb is converted into light and that the surface of the chamber is perfectly absorbing. Find the pressure exerted by the light on the surface of the chamber.
View Solution
