A uniform magnetic field of magnitude 0.20 T exists in space from east to west what speed should a particle of mass 0.010 g and having a charge 1.0X10−5C be projected from south to north so that it moves with a uniform velocity?
To solve the problem, we need to find the speed at which a charged particle should be projected so that it moves with a uniform velocity in a magnetic field. Here are the steps to derive the solution:
Step 1: Identify the forces acting on the particle
When the charged particle enters the magnetic field, two forces act on it:
- The magnetic force (FB) acting upward.
- The gravitational force (Fg) acting downward.
For the particle to move with a uniform velocity, these two forces must be equal in magnitude.
Step 2: Write the expressions for the forces
1. The magnetic force is given by:
FB=Q⋅v⋅B
where Q is the charge of the particle, v is the speed of the particle, and B is the magnetic field strength.
2. The gravitational force is given by:
Fg=m⋅g
where m is the mass of the particle and g is the acceleration due to gravity (approximately 9.81m/s2).
Step 3: Set the forces equal for uniform velocity
For uniform velocity, we set the magnetic force equal to the gravitational force:
Q⋅v⋅B=m⋅g
Step 4: Solve for speed (v)
Rearranging the equation to solve for v:
v=m⋅gQ⋅B
Step 5: Substitute the known values
- Mass (m) = 0.010g=0.010×10−3kg=1.0×10−5kg
- Charge (Q) = 1.0×10−5C
- Magnetic field (B) = 0.20T
- Gravitational acceleration (g) = 9.81m/s2
Substituting these values into the equation:
v=(1.0×10−5kg)⋅(9.81m/s2)(1.0×10−5C)⋅(0.20T)
Step 6: Calculate the speed
Calculating the numerator:
1.0×10−5⋅9.81=9.81×10−5kg m/s2
Calculating the denominator:
1.0×10−5⋅0.20=2.0×10−6C T
Now, substituting back into the equation for v:
v=9.81×10−52.0×10−6=49.05m/s
Final Answer
The speed at which the particle should be projected is approximately:
49.05m/s
When the charged particle enters the magnetic field, two forces act on it:
- The magnetic force (FB) acting upward.
- The gravitational force (Fg) acting downward.
1. The magnetic force is given by:
FB=Q⋅v⋅B
where Q is the charge of the particle, v is the speed of the particle, and B is the magnetic field strength.
Fg=m⋅g
where m is the mass of the particle and g is the acceleration due to gravity (approximately 9.81m/s2).
For uniform velocity, we set the magnetic force equal to the gravitational force:
Q⋅v⋅B=m⋅g
Rearranging the equation to solve for v:
v=m⋅gQ⋅B
- Mass (m) = 0.010g=0.010×10−3kg=1.0×10−5kg
- Charge (Q) = 1.0×10−5C
- Magnetic field (B) = 0.20T
- Gravitational acceleration (g) = 9.81m/s2
v=(1.0×10−5kg)⋅(9.81m/s2)(1.0×10−5C)⋅(0.20T)
Calculating the numerator:
1.0×10−5⋅9.81=9.81×10−5kg m/s2
1.0×10−5⋅0.20=2.0×10−6C T
v=9.81×10−52.0×10−6=49.05m/s
The speed at which the particle should be projected is approximately:
49.05m/s
Topper's Solved these Questions
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER
10 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 1
10 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
Similar Questions
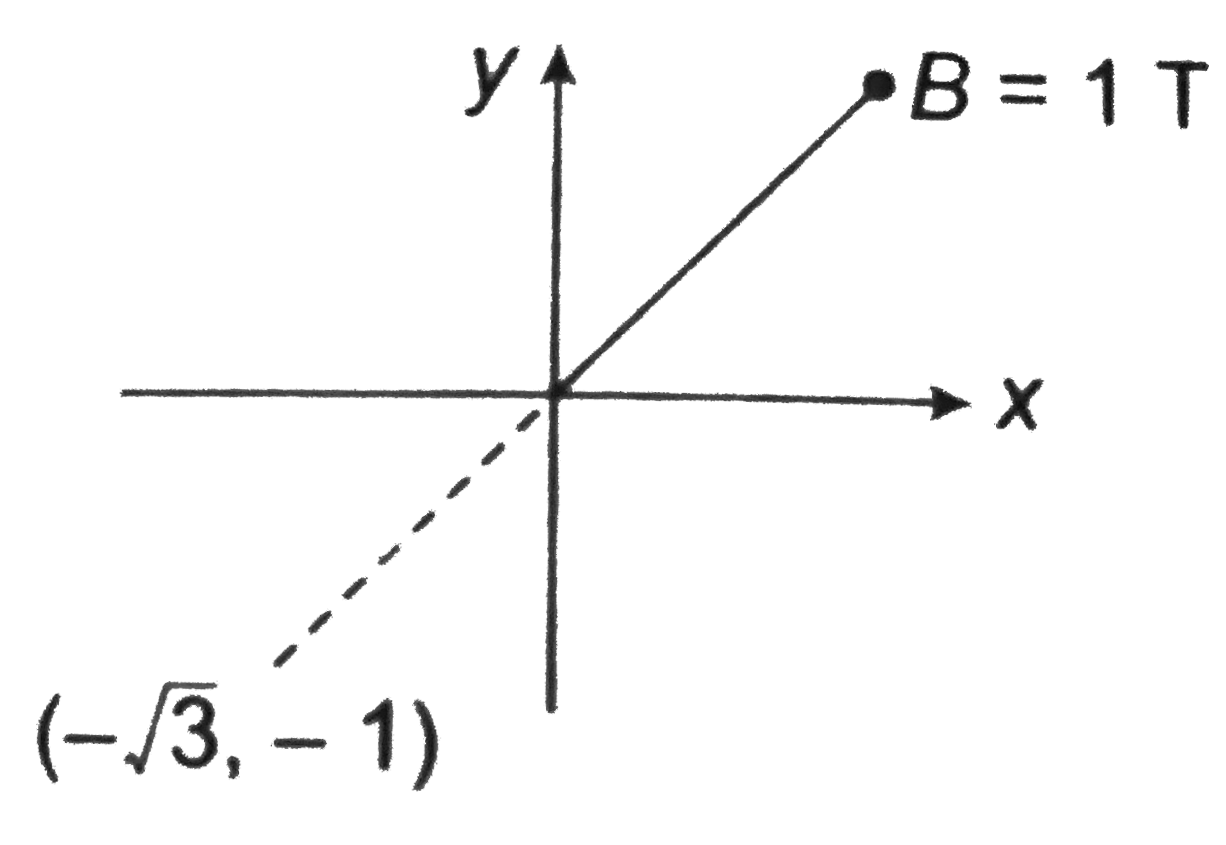
A uniform magnetic field of magnitude 1T exists in region y≥0 along ˆk direction as shown. A particle of charge 1C is projected from point (−√3,−1) towards origin with speeds 1m/sec. If mass of particle moves are:
View SolutionA uniform magnetic field of 0.20×10−3T exists in the space. Find the the change in the magnetic scalar potential as one moves through 50cm along the field.
View SolutionA magnetic field of (4.0X10−3→k) T exerts a force of (4.0→i+3.0→jx10−10 N on a particle having a charge of 1.0X10−9 C and going in the x-y plane. Find the velocity of the particle.
View SolutionA proton enter in a uniform magnetic field of 2.0 mT at an angle of 60degrees with the magnetic field with speed 10m/s. Find the picth of path
View SolutionA uniform magnetic field ¯¯¯B=B0ˆj exists in a space. A particle of mass m and charge q is projected towards negative x-axis with speed v from the a point (d,0,0) The maximum value v for which the particle does not hit y−z plane is .
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionThere exist uniform magnetic and electric fields of manitudes 1T and 1Vm−1 respectively, along positive y-axis. A charged particle of mass 1kg and charge 1C is having velocity 1ms−1 along x-axis and is at origin at t=0. Then, the coordinates of the particle at time πs will be
View SolutionIn a certain region of space there exists a constant and uniform magnetic field of induction B. The width of the magnetic field is a. A charged particle having charge q is projected perpendicular to B and along the width the field. If deflection produced by the fiel perpendicular to the width is d, then the magnitud of the momentum of the particle is,

View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is

View SolutionA particle having a charge20μC and mass 20μg moves along a circle of radius 5.0 cm under the action of a magnetic field 5.0 cm under the action of a magnetic field B = 1.0 T. When the particle is at a point P, a uniform electric field is switched on and it is found that the particla continues on the tangent through P qith a uniform velocity. Find the electric field.
View Solution
