A magnetic field of (4.0X10−3→k) T exerts a force of (4.0→i+3.0→jx10−10 N on a particle having a charge of 1.0X10−9 C and going in the x-y plane. Find the velocity of the particle.
To solve the problem, we need to find the velocity of a charged particle moving in a magnetic field. The force exerted on the particle is given, and we can use the equation for the magnetic force on a charged particle.
1. Identify Given Values:
- Magnetic field, →B=4.0×10−3^k T
- Force, →F=(4.0^i+3.0×10−10^j) N
- Charge, q=1.0×10−9 C
2. Write the Magnetic Force Equation:
The magnetic force →F on a charged particle is given by:
→F=q→v×→B
where →v is the velocity vector of the particle.
3. Assume the Velocity Vector:
Since the particle is moving in the xy-plane, we can express the velocity vector as:
→v=vx^i+vy^j
4. Substitute Known Values into the Force Equation:
(4.0^i+3.0×10−10^j)=(1.0×10−9)(vx^i+vy^j)×(4.0×10−3^k)
5. Calculate the Cross Product:
Using the right-hand rule for the cross product:
^i×^k=−^j,^j×^k=^i
Therefore,
→v×→B=(vx^i+vy^j)×(4.0×10−3^k)=4.0×10−3(−vx^j+vy^i)
6. Substitute the Cross Product Back into the Force Equation:
(4.0^i+3.0×10−10^j)=(1.0×10−9)⋅4.0×10−3(−vx^j+vy^i)
Simplifying gives:
(4.0^i+3.0×10−10^j)=4.0×10−12vy^i−4.0×10−12vx^j
7. Equate Coefficients of ^i and ^j:
For ^i:
4.0=4.0×10−12vy
Solving for vy:
vy=4.04.0×10−12=1012 m/s
For ^j:
3.0×10−10=−4.0×10−12vx
Solving for vx:
vx=−3.0×10−104.0×10−12=−75 m/s
8. Final Velocity Vector:
Combining the components, the final velocity vector is:
→v=−75^i+1012^j m/s
- Magnetic field, →B=4.0×10−3^k T
- Force, →F=(4.0^i+3.0×10−10^j) N
- Charge, q=1.0×10−9 C
The magnetic force →F on a charged particle is given by:
→F=q→v×→B
where →v is the velocity vector of the particle.
Since the particle is moving in the xy-plane, we can express the velocity vector as:
→v=vx^i+vy^j
(4.0^i+3.0×10−10^j)=(1.0×10−9)(vx^i+vy^j)×(4.0×10−3^k)
Using the right-hand rule for the cross product:
^i×^k=−^j,^j×^k=^i
Therefore,
→v×→B=(vx^i+vy^j)×(4.0×10−3^k)=4.0×10−3(−vx^j+vy^i)
(4.0^i+3.0×10−10^j)=(1.0×10−9)⋅4.0×10−3(−vx^j+vy^i)
Simplifying gives:
(4.0^i+3.0×10−10^j)=4.0×10−12vy^i−4.0×10−12vx^j
For ^i:
4.0=4.0×10−12vy
Solving for vy:
vy=4.04.0×10−12=1012 m/s
3.0×10−10=−4.0×10−12vx
Solving for vx:
vx=−3.0×10−104.0×10−12=−75 m/s
Combining the components, the final velocity vector is:
→v=−75^i+1012^j m/s
Topper's Solved these Questions
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER
10 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 1
10 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
Similar Questions
A magnetic field of (4.0×10−3ˆk)T exerts a force (4.0ˆi+3.0ˆj)×10−10N on a particle having a charge 10−9C and moving in the x−y plane. Find the velocity of the particle.
View SolutionA magnetic field of (4.0×10−3ˆk)T exerts a force (4.0ˆi+3.0ˆj)×10−10N on a particle having a charge 10−9C and moving in te x−y plane. Find the velocity of the particle.
View SolutionA uniform magnetic field of magnitude 0.20 T exists in space from east to west what speed should a particle of mass 0.010 g and having a charge 1.0X10−5C be projected from south to north so that it moves with a uniform velocity?
View SolutionA particle having a charge of 2.0X10−8C and a mass of 2.0X10−10g is projected with a speed of 2.0X103ms−1 in a region having a uniform magnetic field of 0.10 T. The velocity is perpendicular to the field. Find the radius of the circle formed by the particle and also the time period.
View SolutionMagnetic force on a charged particle is given by →Fm=q(→v×→B) and electrostatic force →Fe=q→E. A particle having charge q = 1C and mass 1 kg is released from rest at origin. There are electric and magnetic field given by →E=(10ˆi)N/Cforx=1.8m and →B=−(5ˆk)T for 1.8m≤x≤2.4m
A screen is placed parallel to y-z plane at x=3m. Neglect gravity forces.
The speed with which the particle will collide the screen is
View SolutionAs a charged particle 'q' moving with a velocity →v enters a uniform magnetic field →B, it experience a force →F=q(→v×→B).Forθ=0∘or180∘,θ being the angle between →vand→B, force experienced is zero and the particle passes undeflected. For θ=90∘, the particle moves along a circular arc and the magnetic force (qvB) provides the necessary centripetal force (mv2/r). For other values of θ(θ≠0∘,180∘,90∘), the charged particle moves along a helical path which is the resultant motion of simultaneous circular and translational motions.
Suppose a particle that carries a charge of magnitude q and has a mass 4×10−15 kg is moving in a region containing a uniform magnetic field →B=−0.4ˆkT. At some instant, velocity of the particle is →v=(8ˆi−6ˆj4ˆk)×106ms−1 and force acting on it has a magnitude 1.6 N
If the coordinates of the particle at t = 0 are (2 m, 1 m, 0), coordinates at a time t = 3 T, where T is the time period of circular component of motion. will be (take π=3.14)
View SolutionAn experimenter's diary reads as follows: ''a charged particle is projected in a magnetic feld of (7.0→i−3.0→j)X10−3 T. The acceleraation of the particle is found to be (□→i+7.0→j)X10−6ms−2'.Theνmber→≤ftofveci in the last expression was not readable. What can this number be?
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
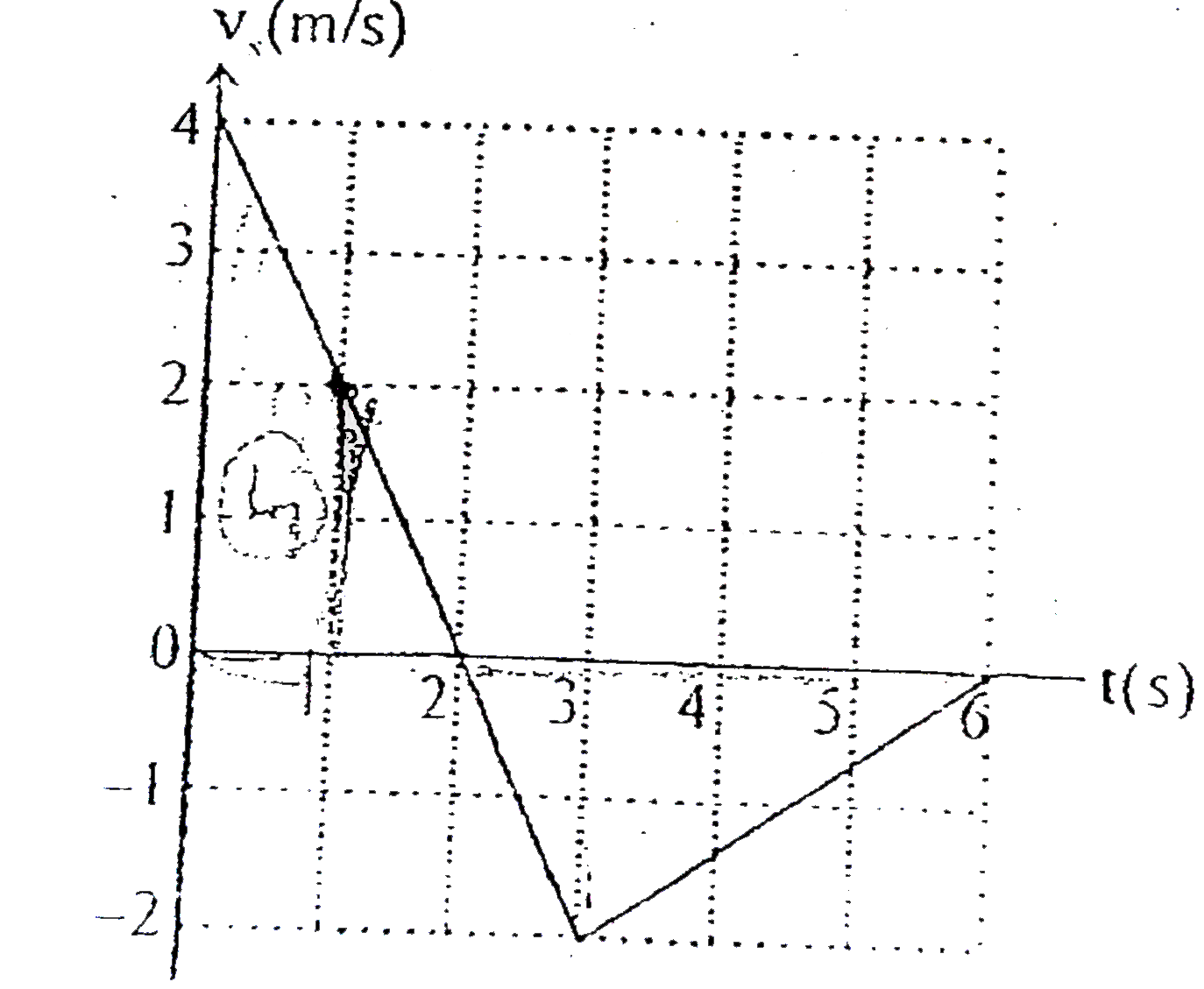
View SolutionA particle of mass m=1.6X10−27 kg and charge q=1.6X10−19 C moves at a speed of 1.0X107ms−7. It enters a region of uniform magnetic field at a point E, as shown in The field has a strength of 1.0 T. (a) The magnetic field is directed into the plane of the paper. The particle leaves the region of the filed at the point F. Find the distance EF and the angle theta. (b) If the field is coming out of the paper, find the time spent by the particle in the regio the magnetic feld after entering it at E.

View SolutionA particle movesin the X-Y plane with a constasnt acceleration of 1.5ms2 in the direction making an angle of 370 with the X-axis.At t=0 the particle is at the orign and its velocity is 8.0 m/s along the X-axis. Find the velocity and the position of the particle at t=4.0 s.

View Solution
