A wire, carrying a current , is kept in the plane along the curve . A magnetic field exists in the z-direction. Find the magnitude of the magnetic force on the portion of the wire between .
To find the magnitude of the magnetic force on the portion of the wire between x=0 and x=λ, we can follow these steps:
Step 1: Understand the Given Information
We have a wire carrying a current i along the curve defined by y=Asin(2πλx) in the x−y plane. A magnetic field B exists in the z-direction.
Step 2: Identify the Force on a Small Element of the Wire
The magnetic force dF on a small segment dL of the wire can be expressed using the formula:
dF=idL×B
Here, dL is a vector along the wire in the direction of the current.
Step 3: Determine the Expression for dL
The wire is parametrized by x and y as y=Asin(2πλx). The differential length element dL can be expressed in terms of dx:
dL=(dx,dy)=(dx,dydxdx)=(dx,A2πλcos(2πλx)dx)
Thus,
dL=(1,A2πλcos(2πλx))dx
Step 4: Calculate the Cross Product
Since the magnetic field B is in the z-direction, we can write:
B=(0,0,B)
The cross product dL×B is calculated as follows:
dF=idL×B=i∣∣
∣
∣∣ijk1A2πλcos(2πλx)000B∣∣
∣
∣∣
Calculating the determinant gives:
dF=iB(A2πλcos(2πλx))dxi
Step 5: Integrate to Find the Total Force
Now, we need to integrate dF from x=0 to x=λ:
F=∫λ0dF=iB∫λ0A2πλcos(2πλx)dx
Calculating the integral:
∫λ0cos(2πλx)dx=(λ2πsin(2πλx))λ0=λ2π(sin(2π)−sin(0))=0
Thus, the total force F is:
F=0
Conclusion
The magnitude of the magnetic force on the portion of the wire between x=0 and x=λ is 0.
---
We have a wire carrying a current i along the curve defined by y=Asin(2πλx) in the x−y plane. A magnetic field B exists in the z-direction.
The magnetic force dF on a small segment dL of the wire can be expressed using the formula:
dF=idL×B
Here, dL is a vector along the wire in the direction of the current.
The wire is parametrized by x and y as y=Asin(2πλx). The differential length element dL can be expressed in terms of dx:
dL=(dx,dy)=(dx,dydxdx)=(dx,A2πλcos(2πλx)dx)
Thus,
dL=(1,A2πλcos(2πλx))dx
Since the magnetic field B is in the z-direction, we can write:
B=(0,0,B)
The cross product dL×B is calculated as follows:
dF=idL×B=i∣∣
∣
∣∣ijk1A2πλcos(2πλx)000B∣∣
∣
∣∣
Calculating the determinant gives:
dF=iB(A2πλcos(2πλx))dxi
Now, we need to integrate dF from x=0 to x=λ:
F=∫λ0dF=iB∫λ0A2πλcos(2πλx)dx
Calculating the integral:
∫λ0cos(2πλx)dx=(λ2πsin(2πλx))λ0=λ2π(sin(2π)−sin(0))=0
Thus, the total force F is:
F=0
The magnitude of the magnetic force on the portion of the wire between x=0 and x=λ is 0.
Topper's Solved these Questions
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - QUESTIONS FOR SHORT ASNWER
10 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective 1
10 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
Similar Questions
A wire, carriying a current I is kept in the x-y plame the curve y -(2 cm) Asin(2πλx).Amag≠ticfieldB∃∈thez−direction.F∈dthemagnitudeofthemag≠ticforceontheportionofthewirebetweenz−−0andx=lambda//2
View SolutionA wire of length L carries a current i along the x-axis. A magnetic field B=B0(ˆi+ˆj+ˆk) exists in the space. Find the magnitude of the magnetic force acting on the wire.
View SolutionA wire loop carrying current I is placed in the x-y plane as shown. Magnetic induction at P is
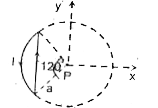
View Solution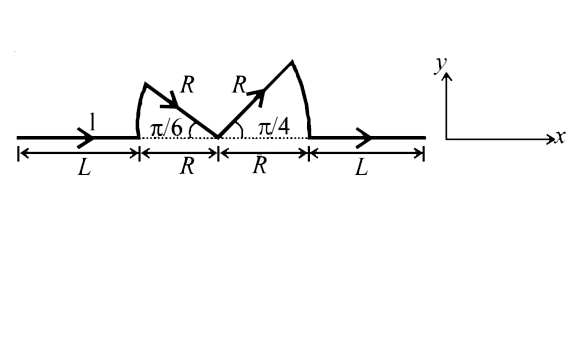
A conductor (shown in the figure) carrying constant current I is kept in the x-y plane in a uniform magnetic field B. If F is the magnitude of the total magnetic force acting on the conductor, then the correct statement is/are
View Solution
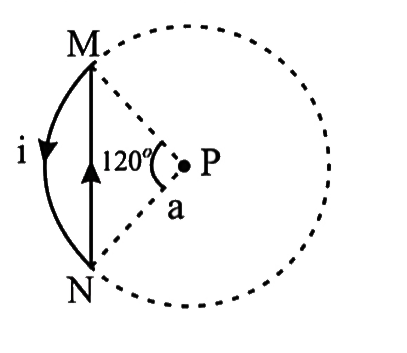
A conducting wire MN carrying a current I is bent into the shape as shown and placed in xy plane. A uniform magnetic field →B=−Bˆk is existing in the region. The net magnetic force experenced by the conducting wire MN is
View SolutionFind the area of the region bounded by the curve y=sinx between x=0andx=2π.
View SolutionA wire of length l carries a current I along the x-asis. A magnetic field exists which is given as →B=B0(→i+→j+→k) T. find the magnitude of the magnetic force acting on the wire.
View SolutionA conductor (shown in the figure) carrying constant current I is kept in the x−y plane in a uniform magnetic field →B. If →F is the magnitude of the total magnetic force acting on the conductor, then the correct statement(s) is (are)

View SolutionA wire loop carrying current I is placed in the x−y plane as shown in the figure. If an external uniform magnetic field →B=Bˆi is switched on, then the torque acting on the loop is
View SolutionThree coplanar parallel wires, each carrying a current of 10 A along the same direction, are placed with a separation 5.0 cm between the consecutive ones. Find the magnitude of the magnetic force per unit length acting on the wires.
View Solution
