A copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8kms−1.
The correct Answer is:A, C
To find the frequencies at which standing longitudinal waves can be set up in a copper rod of length 1.0 m clamped at its middle point, we can follow these steps:
Step 1: Understand the setup
The copper rod is clamped at its middle, which means it will vibrate in such a way that there are nodes at the clamped ends and antinodes at the free ends. The length of the rod is 1.0 m, and since it is clamped at the middle, each half of the rod (L/2) will vibrate.
Step 2: Determine the wavelength
For a rod clamped at the middle, the fundamental mode of vibration will have a wavelength (λ) that is twice the length of each half of the rod. Therefore, we can express the relationship as:
λ2=L2
This leads to:
λ=2L
Substituting the length of the rod (L = 1.0 m):
λ=2×1.0m=2.0m
Step 3: Calculate the fundamental frequency
The speed of sound in copper is given as v=3.8km/s=3800m/s. The frequency (f) can be calculated using the formula:
f=vλ
Substituting the values:
f=3800m/s2.0m=1900Hz
Step 4: Determine higher harmonics
The frequencies of the higher harmonics can be expressed as:
fn=n⋅f0
where f0 is the fundamental frequency and n is a positive integer (1, 2, 3,...). Thus:
fn=n⋅1900Hz
Step 5: Find the range of n
We need to find the values of n such that the frequencies lie between 20 Hz and 20,000 Hz:
1. For n=1:
f1=1⋅1900=1900Hz
2. For n=2:
f2=2⋅1900=3800Hz
3. For n=3:
f3=3⋅1900=5700Hz
4. For n=4:
f4=4⋅1900=7600Hz
5. For n=5:
f5=5⋅1900=9500Hz
6. For n=6:
f6=6⋅1900=11400Hz
7. For n=7:
f7=7⋅1900=13300Hz
8. For n=8:
f8=8⋅1900=15200Hz
9. For n=9:
f9=9⋅1900=17100Hz
10. For n=10:
f10=10⋅1900=19000Hz
Step 6: List the possible frequencies
The possible frequencies between 20 Hz and 20,000 Hz are:
- 1900 Hz
- 3800 Hz
- 5700 Hz
- 7600 Hz
- 9500 Hz
- 11400 Hz
- 13300 Hz
- 15200 Hz
- 17100 Hz
- 19000 Hz
Final Answer
The frequencies at which standing longitudinal waves can be set up in the copper rod are:
- 1900 Hz
- 3800 Hz
- 5700 Hz
- 7600 Hz
- 9500 Hz
- 11400 Hz
- 13300 Hz
- 15200 Hz
- 17100 Hz
- 19000 Hz
The copper rod is clamped at its middle, which means it will vibrate in such a way that there are nodes at the clamped ends and antinodes at the free ends. The length of the rod is 1.0 m, and since it is clamped at the middle, each half of the rod (L/2) will vibrate.
For a rod clamped at the middle, the fundamental mode of vibration will have a wavelength (λ) that is twice the length of each half of the rod. Therefore, we can express the relationship as:
λ2=L2
This leads to:
λ=2L
Substituting the length of the rod (L = 1.0 m):
λ=2×1.0m=2.0m
The speed of sound in copper is given as v=3.8km/s=3800m/s. The frequency (f) can be calculated using the formula:
f=vλ
Substituting the values:
f=3800m/s2.0m=1900Hz
The frequencies of the higher harmonics can be expressed as:
fn=n⋅f0
where f0 is the fundamental frequency and n is a positive integer (1, 2, 3,...). Thus:
fn=n⋅1900Hz
We need to find the values of n such that the frequencies lie between 20 Hz and 20,000 Hz:
1. For n=1:
f1=1⋅1900=1900Hz
2. For n=2:
f2=2⋅1900=3800Hz
3. For n=3:
f3=3⋅1900=5700Hz
4. For n=4:
f4=4⋅1900=7600Hz
5. For n=5:
f5=5⋅1900=9500Hz
6. For n=6:
f6=6⋅1900=11400Hz
7. For n=7:
f7=7⋅1900=13300Hz
8. For n=8:
f8=8⋅1900=15200Hz
9. For n=9:
f9=9⋅1900=17100Hz
10. For n=10:
f10=10⋅1900=19000Hz
The possible frequencies between 20 Hz and 20,000 Hz are:
- 1900 Hz
- 3800 Hz
- 5700 Hz
- 7600 Hz
- 9500 Hz
- 11400 Hz
- 13300 Hz
- 15200 Hz
- 17100 Hz
- 19000 Hz
The frequencies at which standing longitudinal waves can be set up in the copper rod are:
- 1900 Hz
- 3800 Hz
- 5700 Hz
- 7600 Hz
- 9500 Hz
- 11400 Hz
- 13300 Hz
- 15200 Hz
- 17100 Hz
- 19000 Hz
Topper's Solved these Questions
Similar Questions
A cylindrical metal tube has a length of 50 cm and is open at both ends. Find the frequencies between 1000 Hz and 2000 Hz at which the air column in the tube can resonate. Speed of sound in air is 340ms−1.
View SolutionA copper rod of length l=50cm is clamped at its midpoint. Find the number of natural longitudinal oscillations of the rod in the frequency range from 20 to 50kHz. What are those frequencies equal to ?
View Solution
Knowledge Check
A steel rod of length 100 cm is clamped at the middle. The frequency of the fundamental mode for the longitudinal vibrations of the rod is
(Speed of sound in steel = 5 km s−1) a) 1.5 KHz b) 2 KHz c) 2.5 KHz d) 3 KHzA1.5 KHzB2 KHzC2.5 KHzD3 KHz
A person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360ms−1.
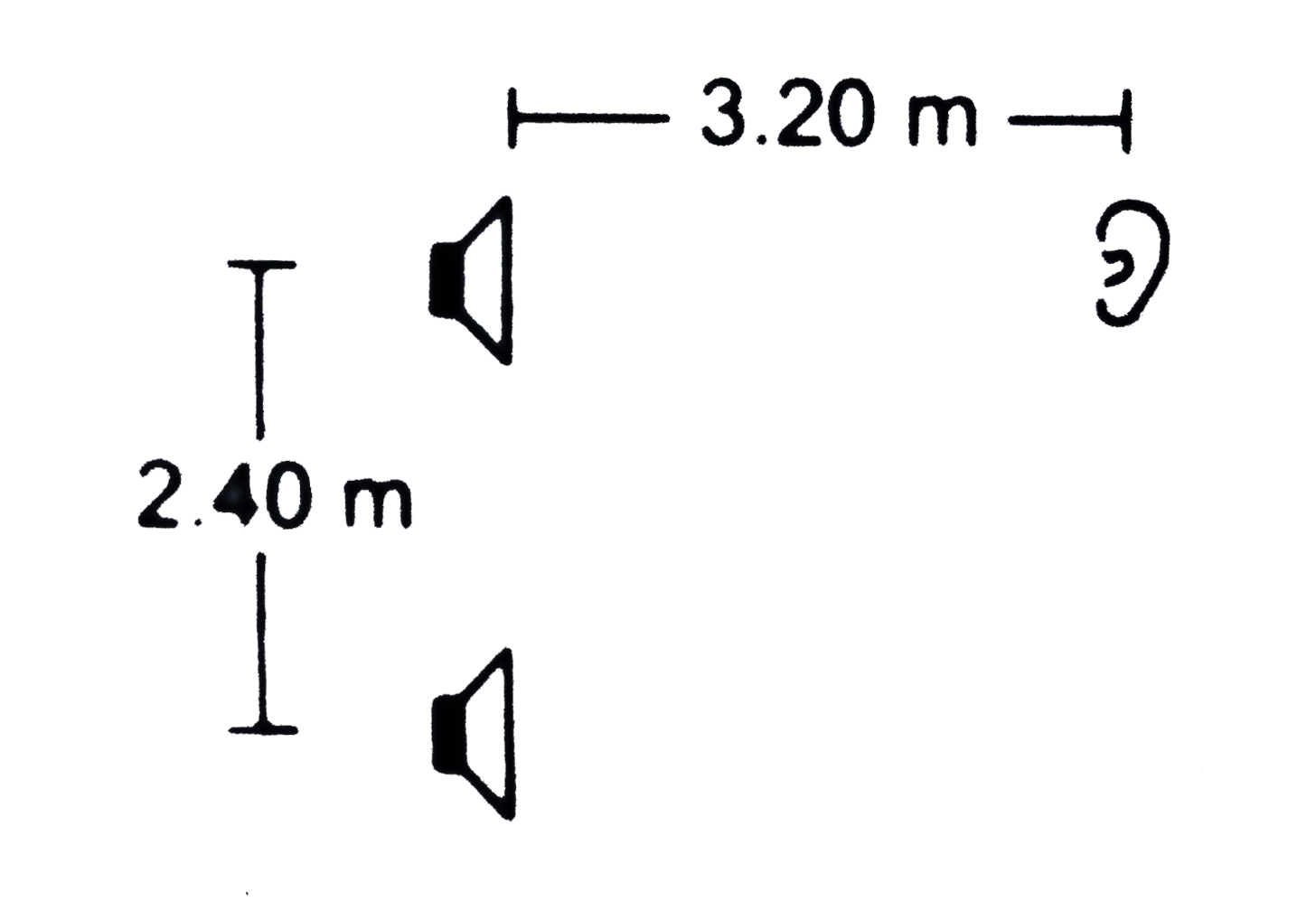
View SolutionTwo stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1
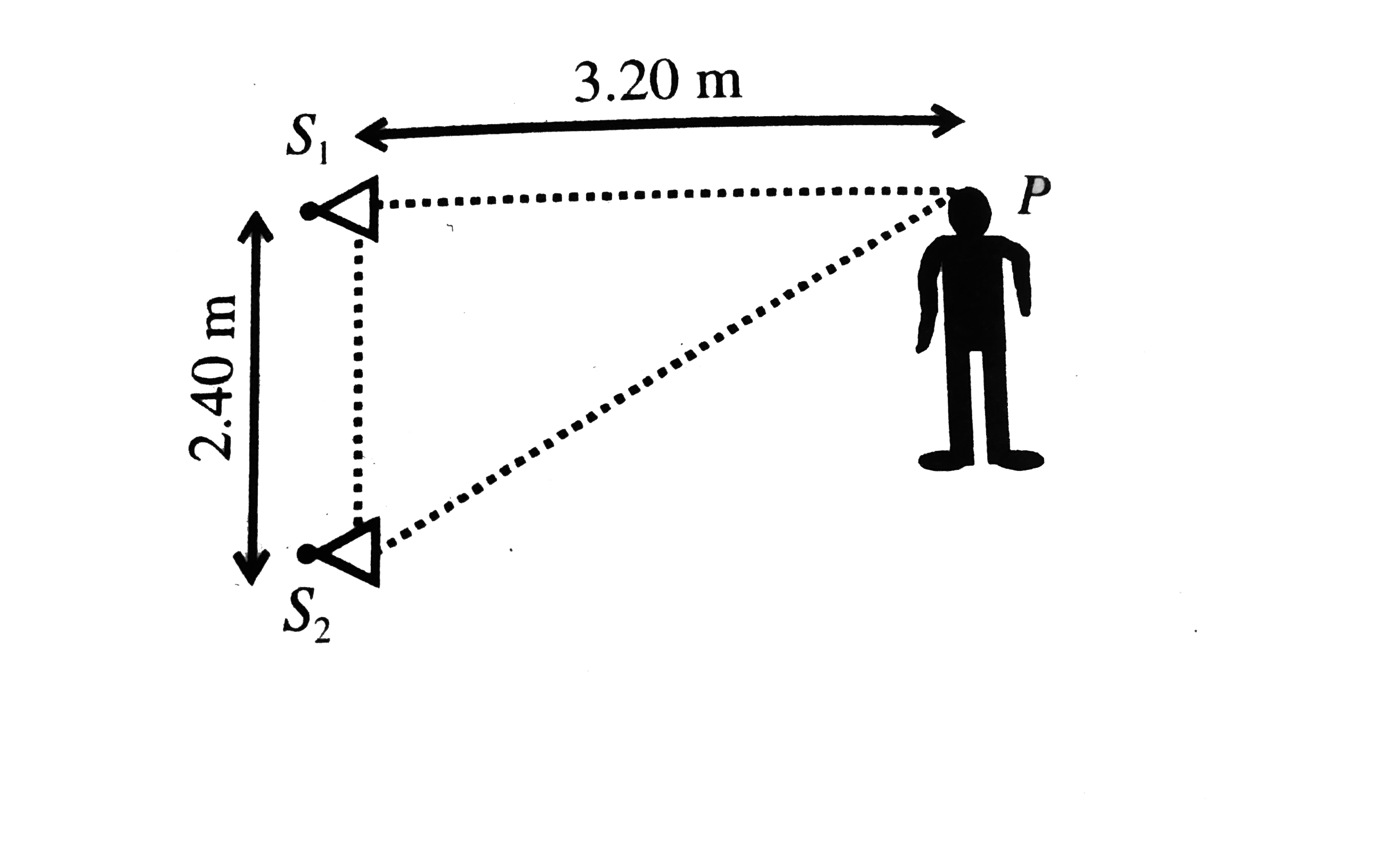
View SolutionTwo stereo speaks S1andS2 are separated by a distance of 2.40m. A person (P) is at a distance of 2.40m. A person (P) is at a distance of 3.20m directly in front of one of the speakers as shown in Fig. 7.8. Find the frequencies in the audible range (20−20,000Hz) for which the listener will hear a minimum sound intensity . Speed of sound in air = 320 m//s.
View SolutionTwo successive resonance frequencies in an open organ pipe are 1944 Hz and 2592 Hz. Find the length of the tube. The speed of sound in air is 324ms−1.
View SolutionA steel rod 100 cm long is clamped at its middle. The fundamental frequency of longitudinal vibrations of the rod is given to be 2.53k Hz. What is the speed of sound in steel?
View SolutionAn electronically driven loudspeaker is placed near the open end of a resonance column apparatus. The length of air column in the tube is 80 cm. The frequency of the loudspeaker can be varied between 20 Hz and 2 kHz. Find the frequencies at which the column will resonate. Speed of sound in air =320ms−1
View SolutionA metallic rod of length 1m is rigidly clamped at its mid point. Longirudinal stationary wave are setup in the rod in such a way that there are two nodes on either side of the midpoint. The amplitude of an antinode is 2×10−6m. Write the equation of motion of a point 2 cm from the midpoint and those of the constituent waves in the rod, (Young,s modulus of the material of the rod =2×1011Nm−2 , density =8000kg−m−3). Both ends are free.
View Solution

