Two stereo speaks S1andS2 are separated by a distance of 2.40m. A person (P) is at a distance of 2.40m. A person (P) is at a distance of 3.20m directly in front of one of the speakers as shown in Fig. 7.8. Find the frequencies in the audible range (20−20,000Hz) for which the listener will hear a minimum sound intensity . Speed of sound in air = 320 m//s. 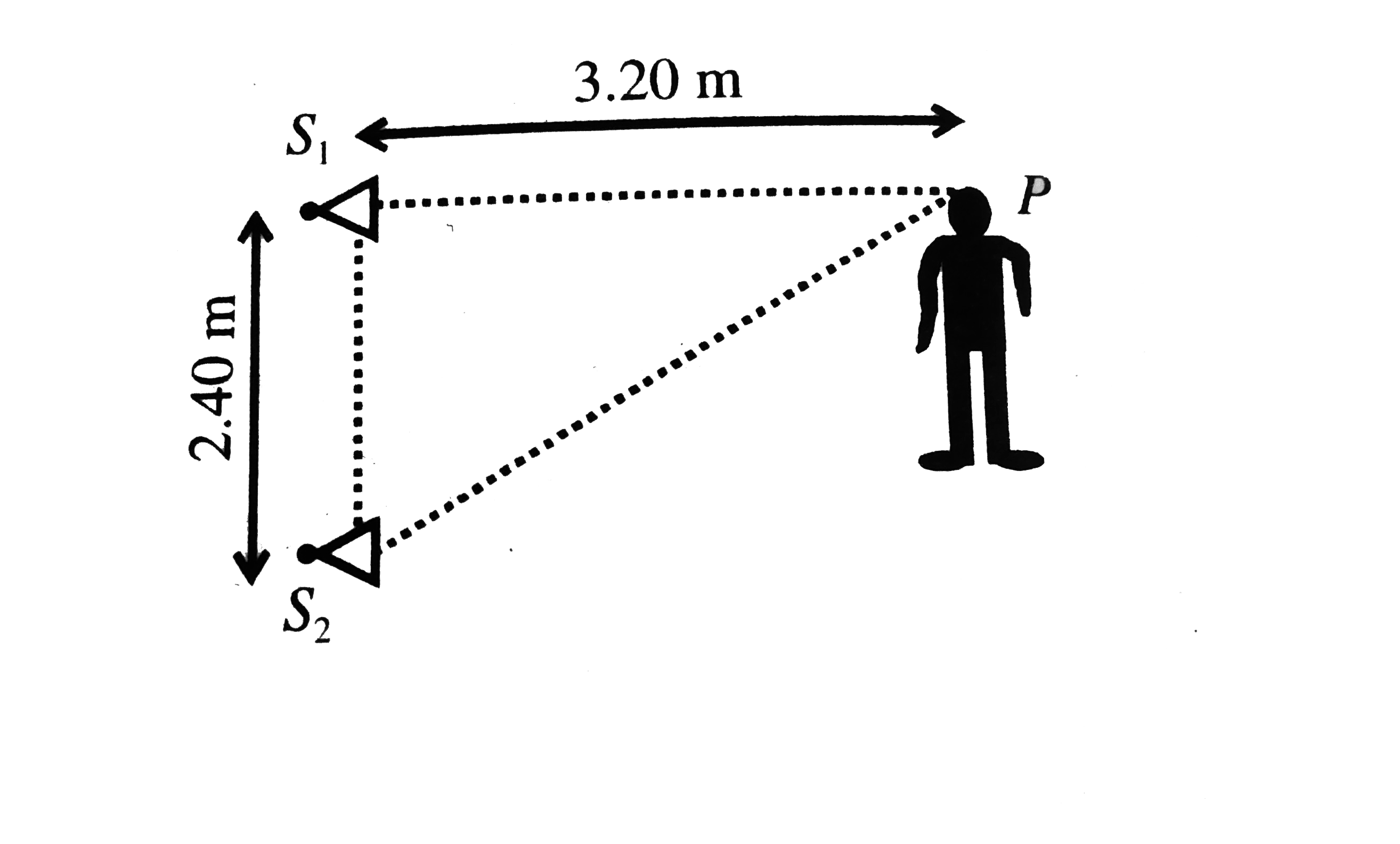
Waves from S1 to S2 reach at point P.
Therefore , the path differnce between waves reaching from S1 to S2 will be Δ=S2P−S1P
Given S1P=3.20m
S2P=√(2.40)2+(3.20)2=4.0m
∴Δ=4.0−3.20=0.80
For minima , path difference
Δ=(2r−1)λ2,r=1,2,3,....
We have λ=v/n , where n is the frequency
Δ=(2r−1)v2n
0.80=(2r−1)v2n
Frequency n=(2r−1)v2×0.80=(2r−1)3201.6Hz=(2r−1)200Hz
Therefore , the required frequencies are n=(2r−1)×200 with r=1,2,....50.
Putting the values of r in the above equation , we get
n=200Hz,600Hz,1000Hz,1400Hz,1800Hz,.....,19800Hz
Similar Questions
Two stereo speakers are separated by a distance of 2.40 m. A person stands at a distance of 3.20 m directly in front of one of the speakers as shown in figure. Find the frequencies in the audible range (20-2000 Hz) for which the listener will hear a minimum sound intensity. Speed of sound in air =320ms−1

View SolutionFind the minimum and maximum wavelengths of sound in water that is in the audible range (20-20000 Hz) for an average human ear. Speed of sound in water =1450ms−1.
View SolutionFind the minimum and maximum wavelengths of sound in water that is in the audible range (20-20000 Hz) for an average human ear. Speed of sound in water =1450ms−1.
View SolutionA copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8kms−1.
View SolutionA soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
View SolutionA person standing at a distance of 6 m from a source of sound receives sound wave in two ways, one directly from the source and other after reflection from a rigid boundary as shown in the figure. The maximum wavelength for which, the person will receive maximum sound intensity, is

View SolutionTwo audio speakers are kept some distance apart and are driven by the same amplifier system. A person is sitting at a place 6.0 m from one of the speakers and 6.4 m from the other. If the sound signal is continuously varied from 500 Hz to 5000 Hz, what are the frequencies for which there is a destructive interference at the place of the listener? Speed of sound in air=320ms−1
View SolutionA person can hear sound waves in the frequency range 20 Hz to 20 kHz. Find the minimum and the maximum wavelengths of sound that is audible to the person. The speed of sound is 360ms−1.
View SolutionThe intensity of sound from a public loud speaker is 1μwatt m−2 at a distance of 5 m. What is the intensity at a distance of 100 m ?
View SolutionA soure of sound of frequency 165 hz is placed in front of a wall at a distance 2 m from it. A dtector is also placed in front of the wall at the same distance from it. Find the minimum distance between the source and detector for which maximum sound is recorded int he detector . the speed of sound is 330 m/s
View Solution
