A 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode.A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air .
The correct Answer is:C, D
To find the tension in the wire, we will follow these steps:
Step 1: Gather the given data
- Length of the wire, Lw=30.0cm=0.30m
- Mass of the wire, Mw=10.0g=0.010kg
- Length of the closed organ pipe, Lp=50.0cm=0.50m
- Speed of sound in air, V=340m/s
Step 2: Calculate the mass per unit length (μ) of the wire
The mass per unit length μ is given by:
μ=MwLw
Substituting the values:
μ=0.010kg0.30m=0.0100.30=0.0333kg/m
Step 3: Calculate the fundamental frequency of the wire (νw)
The fundamental frequency of the wire is given by:
νw=12Lw√Tμ
We will rearrange this equation to solve for T:
T=(2Lwνw)2μ
Step 4: Calculate the fundamental frequency of the closed organ pipe (νp)
The fundamental frequency of the closed organ pipe is given by:
νp=V4Lp
Substituting the values:
νp=340m/s4×0.50m=3402=170Hz
Step 5: Set the frequencies equal (resonance condition)
Since the wire and the organ pipe are in resonance, we have:
νw=νp
Thus:
12Lw√Tμ=170
Step 6: Substitute and solve for T
Substituting Lw=0.30m and μ=0.0333kg/m:
12×0.30√T0.0333=170
This simplifies to:
10.60√T0.0333=170
√T0.0333=170×0.60=102
Squaring both sides:
T0.0333=1022
T=1022×0.0333
Calculating 1022:
1022=10404
Thus:
T=10404×0.0333≈346.8N
Final Answer
The tension in the wire is approximately:
T≈347N
---
- Length of the wire, Lw=30.0cm=0.30m
- Mass of the wire, Mw=10.0g=0.010kg
- Length of the closed organ pipe, Lp=50.0cm=0.50m
- Speed of sound in air, V=340m/s
The mass per unit length μ is given by:
μ=MwLw
Substituting the values:
μ=0.010kg0.30m=0.0100.30=0.0333kg/m
The fundamental frequency of the wire is given by:
νw=12Lw√Tμ
We will rearrange this equation to solve for T:
T=(2Lwνw)2μ
The fundamental frequency of the closed organ pipe is given by:
νp=V4Lp
Substituting the values:
νp=340m/s4×0.50m=3402=170Hz
Since the wire and the organ pipe are in resonance, we have:
νw=νp
Thus:
12Lw√Tμ=170
Substituting Lw=0.30m and μ=0.0333kg/m:
12×0.30√T0.0333=170
This simplifies to:
10.60√T0.0333=170
√T0.0333=170×0.60=102
Squaring both sides:
T0.0333=1022
T=1022×0.0333
Calculating 1022:
1022=10404
Thus:
T=10404×0.0333≈346.8N
The tension in the wire is approximately:
T≈347N
Topper's Solved these Questions
Similar Questions
A tube 1.0m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3m long and a mass of 0.01kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = 330m/s .
View SolutionA closed organ pipe can vibrate at a minimum frequency of 500 Hz. Find the length of the tube. Speed of sound in air =340ms−1.
View Solution
Knowledge Check
A pipe 17 cm long is closed at one end. Which harmonic mode of the pipe resonates a 1.5 kHz source? (Speed of sound in air = 340 m s−1)
AFirstBThirdCFifthDSeventh
A stretched wire is kept near the open end of a closed pipe 0.75 m long. The wire is 0.3 m long and has a mass of 0.01 kg. The wire is made to vibrate in its fundamental node, after Ixing at both ends. It sets the air column in the tube hito vibration at its fundamental frequency by resonance. Find (a) the frequency of oscillation of the air column and 6) the tension in the wire. Velocity of sound =330 m/s.
View SolutionTwo closed organ pipes of length 100 cm and 101 cm 16 beats is 20 sec. When each pipe is sounded in its fundamental mode calculate the velocity of sound
View SolutionFind the greatest length of an organ pipe open at both ends that will have its fundamental frequency in the normal hearing range (20-20,000 Hz). Speed of sound in air =340ms−1.
View SolutionA 40 cm wire having a mass of 3.2 g is stretched between two fixed supports 40.05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1.0mm2, find its Young modulus.
View SolutionA 40 cm wire having a mass of 3.2 g is stretched between two fixed supports 40.05 cm apart. In its fundamental mode, the wire vibrates at 220 Hz. If the area of cross section of the wire is 1.0mm2, find its Young modulus.
View SolutionConsider the situation shown in figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 40ms−1, find the tension in the wire.
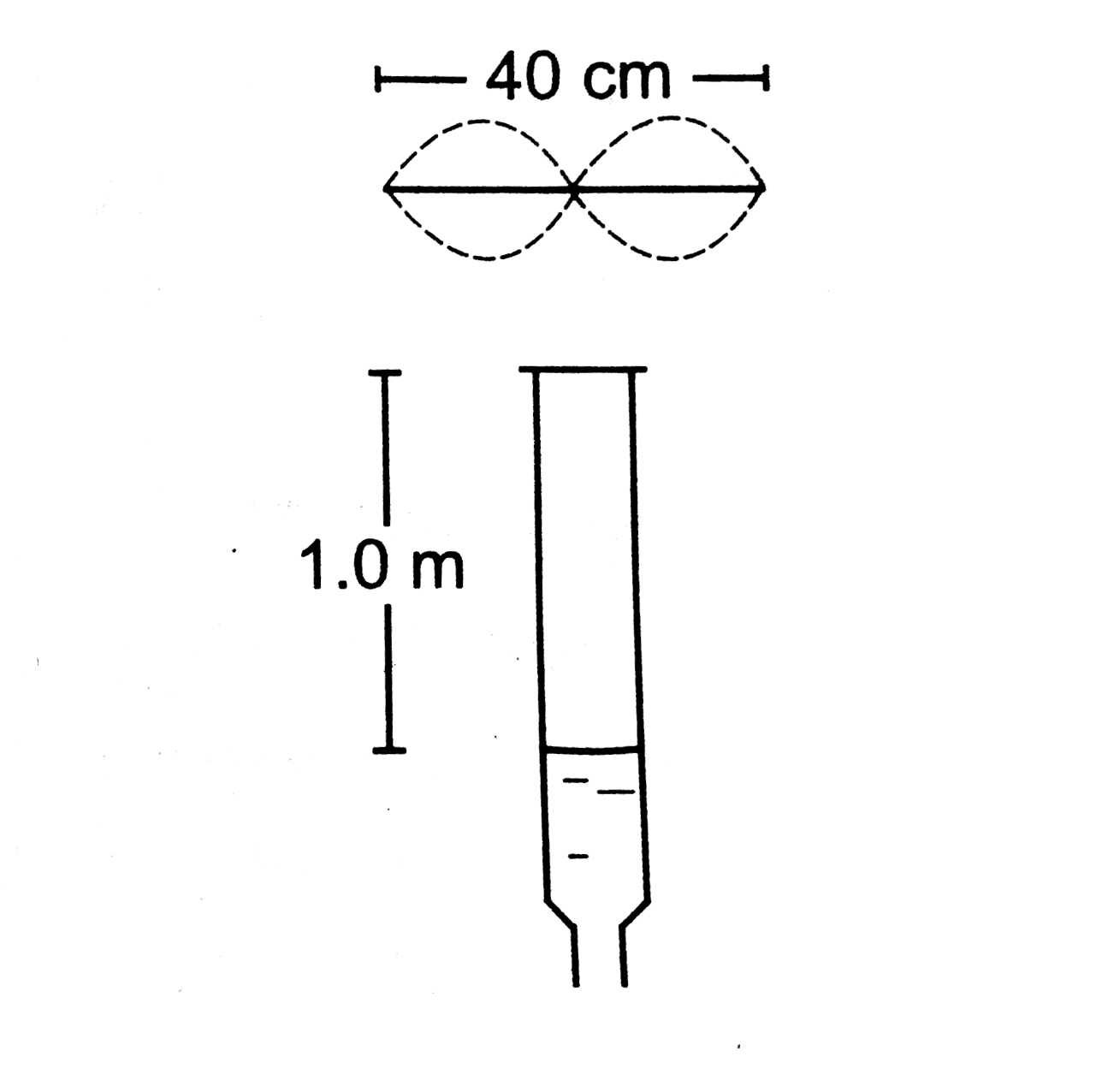 .
.
View SolutionA pipe 20cm long is closed at one end. Which harmonic mode of the pipe is resonantly excited by a 430Hz source? Will the same source be in resonance with the pipe if both ends are open? Take speed of sound in air 340m/s.
View Solution
