A stretched wire is kept near the open end of a closed pipe 0.75 m long. The wire is 0.3 m long and has a mass of 0.01 kg. The wire is made to vibrate in its fundamental node, after Ixing at both ends. It sets the air column in the tube hito vibration at its fundamental frequency by resonance. Find (a) the frequency of oscillation of the air column and 6) the tension in the wire. Velocity of sound =330 m/s.
To solve the problem step by step, we will break it down into two parts: finding the frequency of oscillation of the air column and then calculating the tension in the wire.
Step 1: Calculate the frequency of oscillation of the air column
The fundamental frequency of a closed pipe can be calculated using the formula:
fc=V4L
Where:
- fc = fundamental frequency of the air column
- V = velocity of sound in air (given as 330 m/s)
- L = length of the closed pipe (given as 0.75 m)
Substituting the values into the formula:
fc=330m/s4×0.75m=3303=110Hz
Step 2: Determine the frequency of the wire
Since the wire is made to vibrate in its fundamental mode and sets the air column into vibration at its fundamental frequency by resonance, the frequency of the wire fw is equal to the frequency of the air column fc.
Thus,
fw=fc=110Hz
Step 3: Calculate the mass per unit length of the wire
The mass per unit length μ of the wire can be calculated using the formula:
μ=mL
Where:
- m = mass of the wire (given as 0.01 kg)
- L = length of the wire (given as 0.3 m)
Substituting the values:
μ=0.01kg0.3m=0.0333kg/m
Step 4: Calculate the tension in the wire
The fundamental frequency of the stretched wire can be expressed as:
fw=12L√Tμ
Rearranging this to find the tension T:
T=(2Lfw)2μ
Substituting the values:
- L=0.3m
- fw=110Hz
- μ=0.0333kg/m
Calculating:
T=(2×0.3m×110Hz)2×0.0333kg/m
Calculating 2×0.3×110:
=66m/s
Now squaring it:
=4356m2/s2
Now multiplying by μ:
T=4356×0.0333≈145.2N
Final Answers:
(a) The frequency of oscillation of the air column is 110Hz.
(b) The tension in the wire is 145.2N.
---
- fc = fundamental frequency of the air column
- V = velocity of sound in air (given as 330 m/s)
- L = length of the closed pipe (given as 0.75 m)
- m = mass of the wire (given as 0.01 kg)
- L = length of the wire (given as 0.3 m)
- fw=110Hz
- μ=0.0333kg/m
(a) The frequency of oscillation of the air column is 110Hz.
Topper's Solved these Questions
- WAVESBook:ICSEChapter:WAVESExercise:Musical Sound
Explore 2 Videos
- WAVESBook:ICSEChapter:WAVESExercise:Conceptual Short Answer Questions With Answers
Explore 25 Videos
- WAVESBook:ICSEChapter:WAVESExercise:Additional Solved Problems
Explore 13 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS Book:ICSEChapter:VECTORS SCALARS ELEMENTARY CALCULUS Exercise:UNSOLVED PROBLEMS
Explore 79 Videos
Similar Questions
A tube 1.0m long is closed at one end. A stretched wire is placed near the open end. The wire is 0.3m long and a mass of 0.01kg . It is held fixed at both ends and vibrates in its fundamental mode. It sets the air column in the tube into vibration at its fundamental frequency by resonance. Find
(a) the frequency of oscillation of the air column and
(b) the tension in the wire.
Speed of sound in air = 330m/s .
View SolutionConsider the situation shown in figure. The wire which has a mass of 4.00 g oscillates in its second harmonic and sets the air column in the tube into vibrations in its fundamental mode. Assuming that the speed of sound in air is 40ms−1, find the tension in the wire.
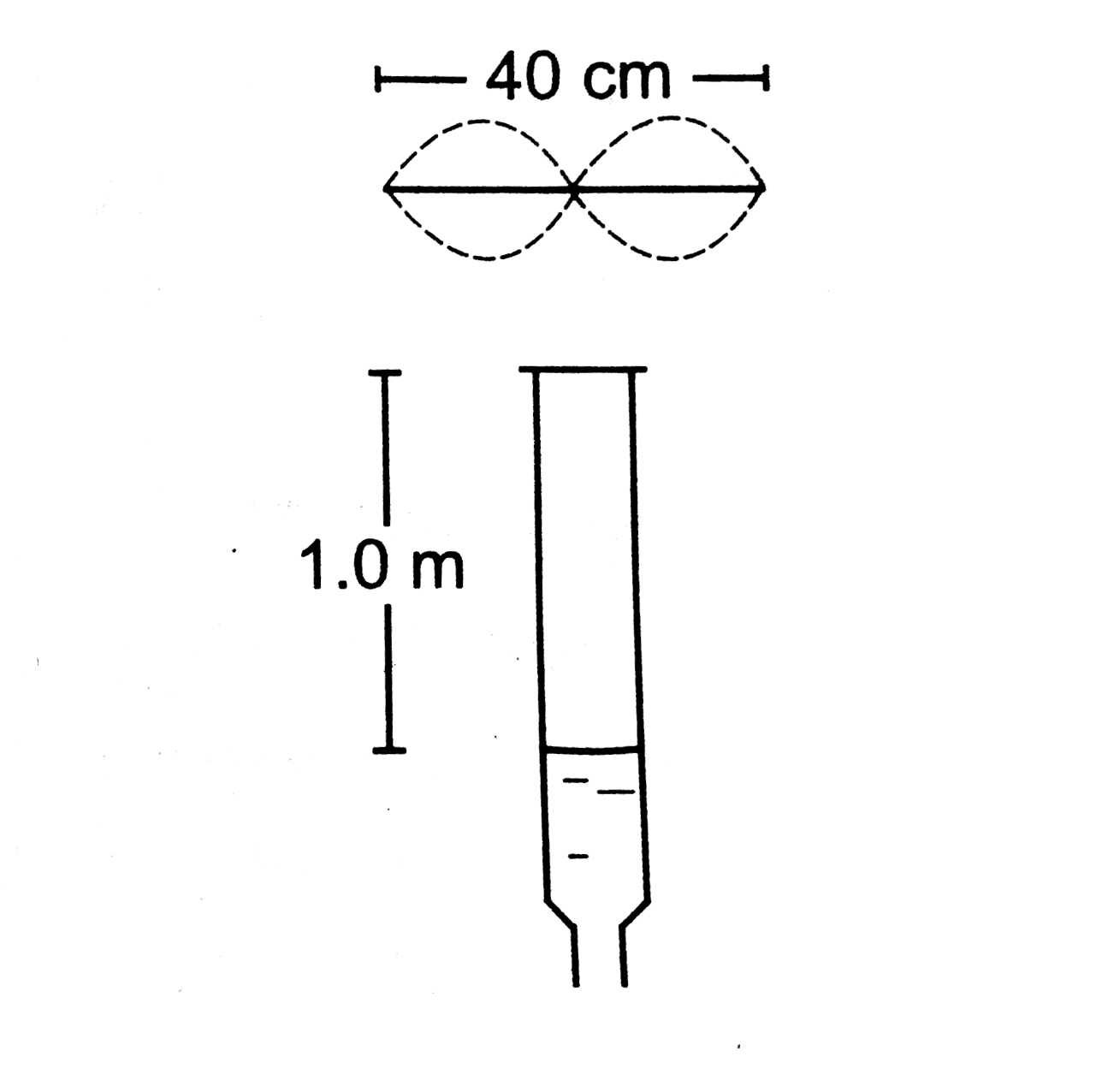 .
.
View SolutionA wire of length 40cm which has a mass of 4 g oscillates in its second harmonic and sets the air column in the tube to vibrations in its funrations in its fundamental mode as shows in figure. Assuming the speed of sound in air as 340m/s . Find the tension in the wire.

View SolutionA wire of length 40 cm which has a mass of 4 gms oscillates in its second harmonic and sets the air column in the tube to vibrations in its fundamental mode as shown in figure. Assuming speed of sound in air as 340 m/s, find the tension in the wire.

View SolutionIf the fundamental frequency of a pipe closed at one is 512HZ . The frequency of a pipe of the same dimension but open at both ends will be
View SolutionA 30.0-cm-long wire having a mass of 10.0 g is fixed at the two ends and is vibrated in its fundamental mode.A 50.0-cm-long closed organ pipe, placed with its open end near the wire, is set up into resonance in its fundamental mode by the vibrating wire. Find the tension in the wire. Speed of sound in air =340ms−1.
View SolutionFind the fundamental frequency and the frequency of the third overtone of a pipe 45 cm long. If the pipe is open at both ends (use V=344m/s)
View SolutionCalculate the frequency of the fundamental note of 0.35m long open and closed pipes? Velocity of sound is 340ms−1.
View SolutionAn open organ pipe has fundamental frequency
100 Hz. What frequency will be produced if its one
end is closed ?
View SolutionThe separation between a node and the next antinode in a vibrating air column is 25 cm. If the speed of sound in air is 340ms−1, find the frequency of vibration of the air column.
View Solution

