A metallic rod of length 1m is rigidly clamped at its mid point. Longirudinal stationary wave are setup in the rod in such a way that there are two nodes on either side of the midpoint. The amplitude of an antinode is 2×10−6m. Write the equation of motion of a point 2 cm from the midpoint and those of the constituent waves in the rod, (Young,s modulus of the material of the rod =2×1011Nm−2 , density =8000kg−m−3). Both ends are free.
(i) y=2×10−6cos5π(0.5±0.02)sin25000πt,
(ii) y1=10−6sin(25000πt−5πx),y2=10−6sin(25000πt+5πx)
y,y1,y2& x are in m & t is in sec
As found in case of strings, in case of rods also the clamped point behave as a node while the free end antinode. The situation is shown in the figure
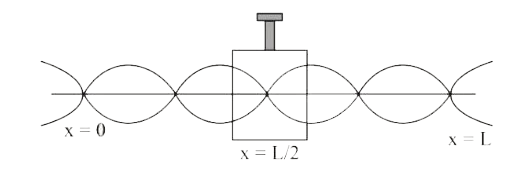
Because the distance between two consecutive nodes is (λ/2) while between a node and antinode is λ/4, hence
4×[λ2]+2[λ4]=Lorλ=2×15=0.4m
Further, it is given that Y=2×1011N/m2andρ=8×103kg/m3
v=√Yρ=√2×10118×103=5000m/s
Hence, from v=nλ,n=vλ=50000A=12500Hz
Now if incident and reflected waves along the rod are y1=Asin(ωt−kx)andy2=Asin(ωt+kx+ϕ)
The resultant will be y=y1+y2=A[sin(ωt−kx)+sin(ωt+kx+ϕ)]=2Acos(kx+ϕ2)sin(ωt+ϕ2)
Because there is an antinode at the free end of the rod, hence amplitude is maximum at x=0, So
cos(k×0+ϕ2)=maximum=1 i.e., ϕ=0
And Amax=2A=2×10−6m(given)
y=2×10−6cos[2πxλ]sin(2πnt)
Putting values of λandn, we get y=2×10−6cos5πxsin25000πt
Now, because for a point 2 cm from the midpoint x=(0.50±0.02)
Hence y=2×10−6cos5π(0.5±0.02)sin25000πt.
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (TRUE FALSE TYPE)4videos
WAVE MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - WAVE MOTIONEXERCISE - JEE ADVANCED ARCHIVE LEVEL 2 (NUMERICAL VALUE TYPE)21videos
WAVE MOTION
- BOOK - VMC MODULES ENGLISHCHAPTER - UNITS, MEASUREMENTS & ERRORSEXERCISE - IN - CHAPTER EXERCISE - B10videos
UNITS, MEASUREMENTS & ERRORS
- BOOK - VMC MODULES ENGLISHCHAPTER - WORK ENERGY AND POWER EXERCISE - IMPECCABLE54videos
WORK ENERGY AND POWER
Similar Questions
At which point of a stationary wave the sound heard is maximum, at the node or the antinode ?
View SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The magnitude of strain at midpoint of the rod at t=1sec isView SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing stress developed in the rod isView SolutionA metallic rod of length 1m has one end free and other end rigidly clamped. Longitudinal stationary waves are set up in the rod in such a way that there are total six antinodes present along the rod. The amplitude of an antinode is 4×10−6m. young's modulus and density of the rod are 6.4×1010N/m2 and 4×103Kg/m3 respectively. Consider the free end to be at origin and at t=0 particles at free end are at positive extreme.
The equation describing displacements of particles about their mean positions is.View SolutionA metallic rod of length 1 m, young's modulus 3×1011Nm−3 and density is 7.5×102kgm3clamped at its middle. Longitudinal stationary vibrations are produced in the rod with the total number of displacement nodes equal to 3. The frequency of vibrations is
View SolutionIn a standing wave the phase difference between two points on either side of a a node will be
View SolutionA copper rod of length 1.0 m is clamped at its middle point. Find the frequencies between 20 Hz and 20,000 Hz at which standing longitudinal waves can be set up in the rod. The speed of sound in copper is 3.8kms−1.
View SolutionIn a stationary longitudinal wave, nodes are points of
View SolutionA rod of nickel of length l is clamped at its midpoint . The rod is stuck and vibrations are set up in the rod . Find the general expression for the frequency of the longitudinal vibrations of the rod . Young's modulus and density of the rod is Yandρ , respectively.
View SolutionA copper rod of length l=50cm is clamped at its midpoint. Find the number of natural longitudinal oscillations of the rod in the frequency range from 20 to 50kHz. What are those frequencies equal to ?
View Solution


