Find the thickness of a plate which will produce a change in optical path equal to half the wavelength λ of the light passing through it normally. The refractive index of the plate is μ.
The correct Answer is:A, B, D
To find the thickness of a plate that produces a change in optical path equal to half the wavelength of light passing through it normally, we can follow these steps:
1. Understand the Problem: We need to find the thickness t of a plate such that the change in optical path Δx is equal to λ2, where λ is the wavelength of the light. The refractive index of the plate is given as μ.
2. Write the Optical Path Difference Formula: The optical path difference Δx when light passes through a medium is given by the formula:
Δx=(μ−1)t
where μ is the refractive index of the plate and t is the thickness of the plate.
3. Set Up the Equation: According to the problem, we have:
Δx=λ2
Therefore, we can set up the equation:
(μ−1)t=λ2
4. Rearrange to Solve for Thickness t: We can rearrange the equation to solve for t:
t=λ2μ−1
Simplifying this gives:
t=λ2(μ−1)
5. Final Expression: Thus, the thickness t of the plate that produces a change in optical path equal to half the wavelength of light is given by:
t=λ2(μ−1)
Final Answer:
The thickness of the plate is t=λ2(μ−1).
Δx=(μ−1)t
where μ is the refractive index of the plate and t is the thickness of the plate.
Δx=λ2
Therefore, we can set up the equation:
(μ−1)t=λ2
t=λ2μ−1
Simplifying this gives:
t=λ2(μ−1)
t=λ2(μ−1)
The thickness of the plate is t=λ2(μ−1).
Topper's Solved these Questions
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Question for short Answer
11 Videos
- LIGHT WAVESBOOK - HC VERMA ENGLISHCHAPTER - LIGHT WAVESEXERCISE - Objective -2
10 Videos
- GEOMETRICAL OPTICSBOOK - HC VERMA ENGLISHCHAPTER - GEOMETRICAL OPTICSEXERCISE - Question For short Answer
18 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
Similar Questions
The ratio of thickness of plates of two transparent medium A and B is 6 : 4. If light takes equal time in passing through them, then refractive index of A with respect to B will be
View SolutionWhen a mica plate of thickness 0.1mm is introduced in one of the interfering beams, the central fringe is displaced by a distance equal to 10 fringes. If the wavelength of the light is 6000A0, the refractive index of the mica is
View SolutionA long solenoid having n = 200 turns per metre has a circular cross-section of radius a1=1cm. A circular conducting loop of radius a2=4cm and resistance R=5(Ω) encircles the solenoid such that the centre of circular loop coincides with the midpoint of the axial line of the solenoid and they have the same axis as shown in Fig.
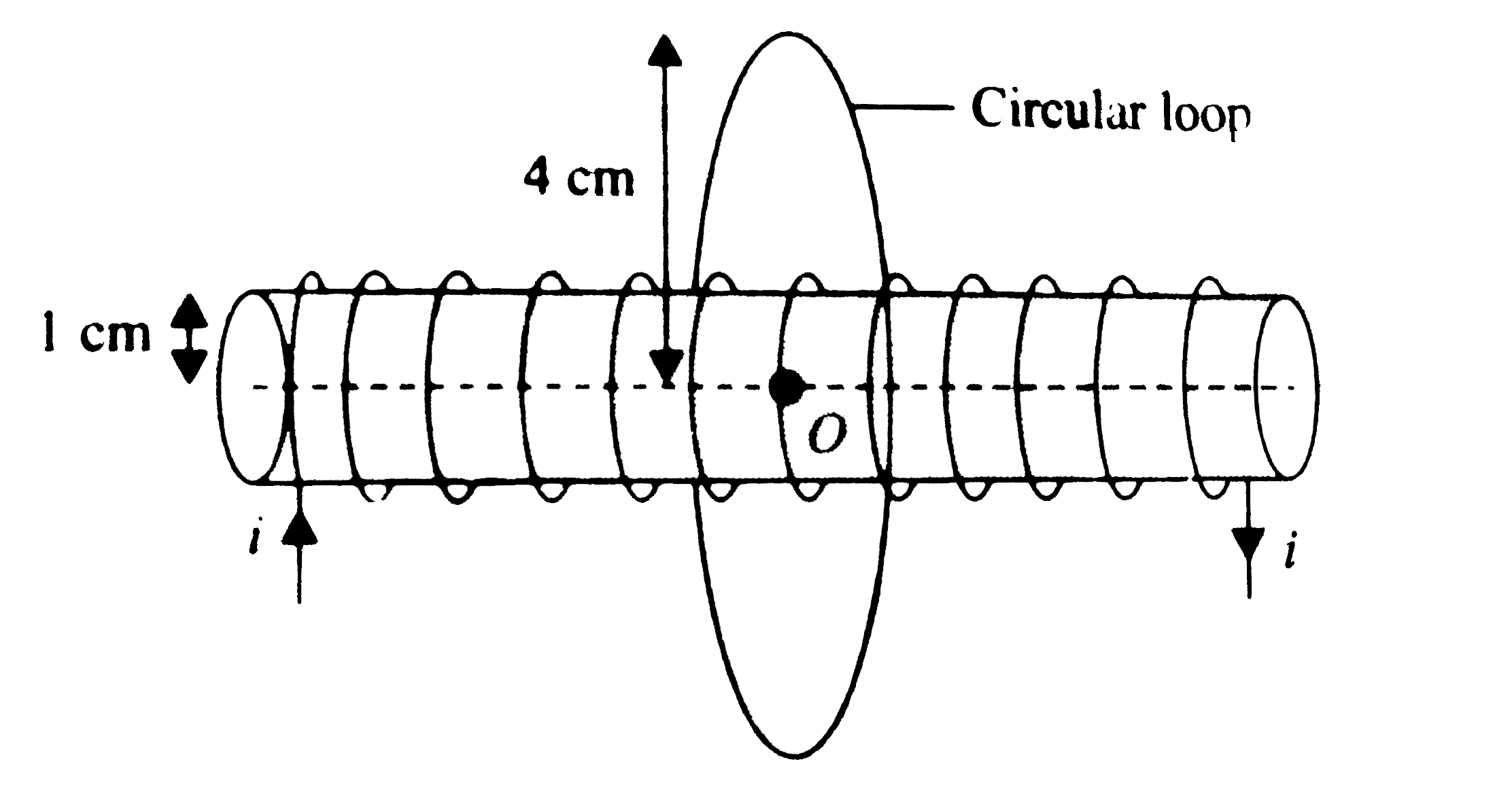
A current 't' in the solenoid results in magnetic field along its axis with magnitude B=(μ)ni at points well inside the solenoid on its axis. We can neglect the insignificant field outside the solenoid. This results in a magnetic flux (ϕ)B through the circular loop. If the current in the winding of solenoid is changed, it will also change the magnetic field B=(μ)0ni and hence also the magnetic flux through the circular loop. Obvisouly, it will result in an induced emf or induced electric field in the circular loop and an induced current will appear in the loop. Let current in the winding of solenoid be reduced at a rate of 75A/sec.
When the current in the solenoid becomes zero so that external magnetic field for the loop stops changing, current in the loop will follow a differenctial equation given by [You may use an approximation that field at all points in the area of loop is the same as at the centre
View SolutionFind the minimum thickness of a film which will strongly reflect the light of wavelength 589 nm. The refractive index of the material of the film is 1.25.
View SolutionA plate of thickness t made of a material of refractive index μ is placed in front of one of the slits in a double slit experiment. (a) Find the changes in he optical path due to introduction of the plate. (b) Wht should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero ? Wavelength of the light used is λ. Neglect any absorption of light in the plate.
View SolutionA plate of thickness t made of a material of refractive index μ is placed in front of one of the slits in a double slit experiment. (a) Find the changes in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the center of the fringe pattern zero ? Wavelength of the light used is λ. Neglect any absorption of light in the plate.
View SolutionThe angles of incidence and refraction of a monochromatic ray of light of wavelength λ at an air-glass interface are i and r, respectively. A parallel beam of light with a small spread δλ in wavelength about a mean wavelength λ is refracted at the same air-glass interface. The refractive index μ of glass depends on the wavelength λ as μ(λ)=a+b/λ2 where a and b are constants. Then the angular spread in the angle of refraction of the beam is
View SolutionIn Young's double slit experiment, the fringes are displaced index 1.5 is introduced in the path of one of the beams. When this plate in replaced by another plate of the same thickness, the shift of fringes is (3/2)x. The refractive index of the second plate is
View SolutionA ray of light passes through a prism in a principle plane the deviation being equal to angle of incidence which is equal to 2α. It is given that α is the angle fo prism and μ is the refractive index of the material of prism, then
View SolutionA lens with a focal length of f=30cm produces on a screen a sharp image of an object that is at a distance of a=40cm from the lens. A plane parallel plate with thickness of d=9cm is placed between the lens and the object perpendicular to the optical axis of the lens. Through what distance should the screen be shifted for the image of the object to remain distinct? The refractive index of the glass of the plate is μ=1.8.
View Solution
