The ratio of thickness of plates of two transparent medium A and B is 6 : 4. If light takes equal time in passing through them, then refractive index of A with respect to B will be
1.4
1.5
1.75
1.33
The correct Answer is:2
To find the refractive index of medium A with respect to medium B given the ratio of thicknesses and the condition that light takes equal time to pass through both mediums, we can follow these steps:
1. Understand the Given Information:
- The ratio of thicknesses of the two mediums A and B is given as:
dAdB=64=32
- The time taken for light to pass through both mediums is equal:
tA=tB
2. Relate Speed, Distance, and Time:
- The speed of light in a medium can be expressed as:
v=dt
- Therefore, for medium A:
vA=dAtA
- And for medium B:
vB=dBtB
3. Since the times are equal:
- We can write:
vA=dAtandvB=dBt
- Here, t is the common time taken for both mediums.
4. Express the Refractive Index:
- The refractive index μ of a medium is given by:
μ=cv
- Therefore, the refractive indices of A and B can be expressed as:
μA=cvAandμB=cvB
5. Find the Ratio of Refractive Indices:
- The ratio of refractive indices μAμB can be expressed as:
μAμB=vBvA
6. Substituting the Speeds:
- Substitute the expressions for vA and vB:
μAμB=dBtdAt=dBdA
7. Using the Thickness Ratio:
- From the thickness ratio dAdB=32, we can find:
dBdA=23
8. Final Calculation:
- Thus, we have:
μAμB=dBdA=23
9. Conclusion:
- Therefore, the refractive index of medium A with respect to medium B is:
μA/B=23≈0.666
- The ratio of thicknesses of the two mediums A and B is given as:
dAdB=64=32
- The time taken for light to pass through both mediums is equal:
tA=tB
- The speed of light in a medium can be expressed as:
v=dt
- Therefore, for medium A:
vA=dAtA
- And for medium B:
vB=dBtB
- We can write:
vA=dAtandvB=dBt
- Here, t is the common time taken for both mediums.
- The refractive index μ of a medium is given by:
μ=cv
- Therefore, the refractive indices of A and B can be expressed as:
μA=cvAandμB=cvB
- The ratio of refractive indices μAμB can be expressed as:
μAμB=vBvA
- Substitute the expressions for vA and vB:
μAμB=dBtdAt=dBdA
- From the thickness ratio dAdB=32, we can find:
dBdA=23
- Thus, we have:
μAμB=dBdA=23
- Therefore, the refractive index of medium A with respect to medium B is:
μA/B=23≈0.666
Topper's Solved these Questions
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-1
1 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-2
1 Videos
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
Similar Questions
The speed of light in a transparent medium is 0.6 times that of its speed in vacuum. What is the refractive index of the medium?
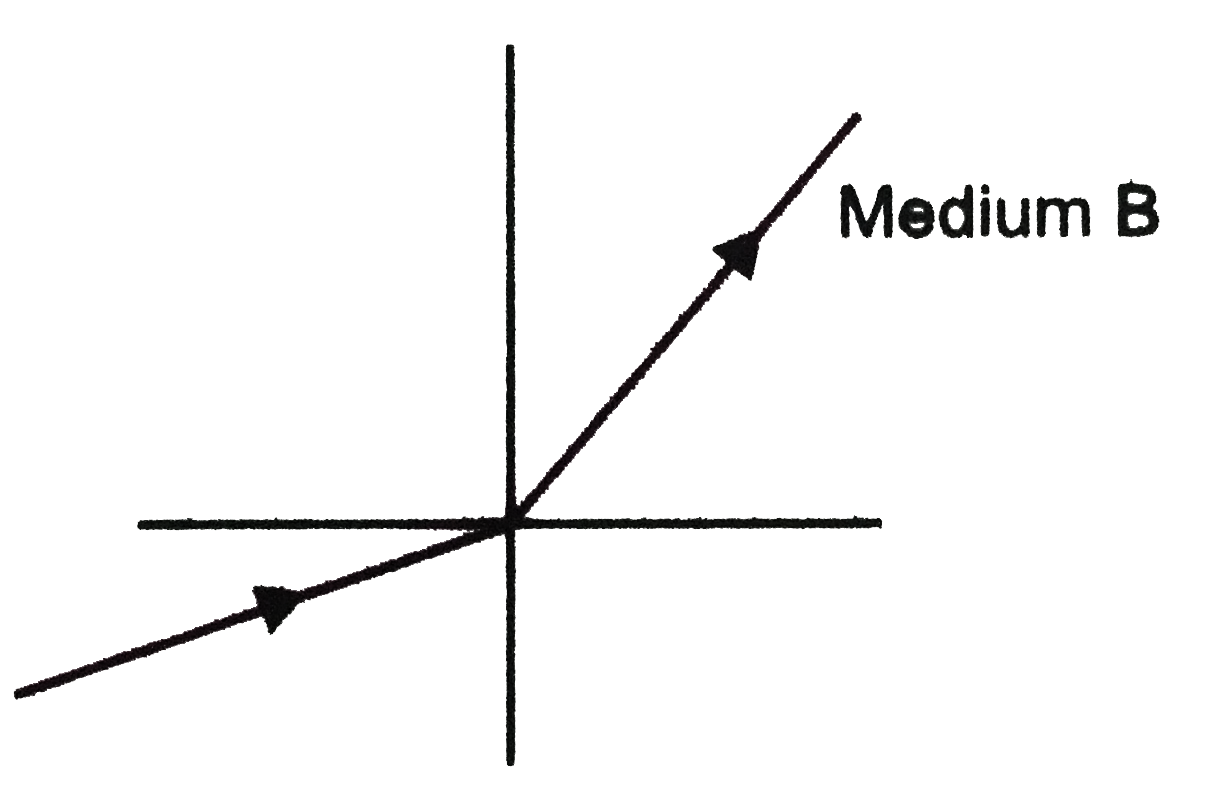
View SolutionA light ray enters from medium A to medium B as shown in Figure. The refractive index of medium A relative to B will be
View SolutionFind the thickness of a plate which will produce a change in optical path equal to half the wavelength λ of the light passing through it normally. The refractive index of the plate is μ.
View SolutionThe critical angle between a certain transparent medium and air is ϕ. A ray of light travelling through air enters the medium at an angle of incidence equal to its Brewster angle θ. Therefore, the angle of refraction is
View SolutionThe critical angle between a certain transparent medium and air is ϕ. A ray of light travelling through air enters the medium at an angle of incidence equal to its Brewster angle θ. Therefore, the angle of refraction is
View SolutionTime taken by sunlight to pass through a window of thickness 4mm whose refraactive index is 32, is
View Solution(a) State Snell's law of refraction of light.
(b) A transparent medium A floats on another transparent medium B. When a ray of light travels obliquely from A into B, the refracted ray bends away from from the normal. Which of these two media A or B are optically denser and why ?
View SolutionA ray of light is incident on the surface of a glass plate at an angle of incidence equal to Brewster's angle ϕ. If μ represents the refractive index of glass with respect to air, then the angle between reflected and refracted rays is
View SolutionHow is the refractive index of a medium related to the speed of light ? Obtain an expression for refractive index of a medium with respect to another in terms of speed of light in these two media ?
View SolutionDefine refractive index of a transparent medium. A ray of light passes through a triangular prism. Plot a graph showing the variation of angle of deviation with the angle of incidence.
View Solution
