A man can see the objects upto a distance of one metre from his eyes. For correcting his eye sight so that he can see an object at infinity, he requires a lens whose power is
+0.5D
+1.0
+2.0
−1.0D
The correct Answer is:4
To solve the problem, we need to determine the power of the lens required for a man who can only see objects up to a distance of 1 meter, so that he can see objects at infinity.
1. Identify the Given Information:
- The maximum distance at which the man can see clearly (near point) is d=1m.
- He wants to see objects at infinity, which means the object distance u=−∞ (the negative sign indicates that the object is on the same side as the incoming light).
2. Determine the Image Distance:
- For the man to see an object at infinity, the image must be formed at his near point, which is v=−1m (again, the negative sign indicates that the image is formed on the same side as the object).
3. Use the Lens Formula:
- The lens formula is given by:
1f=1v−1u
- Substitute the values of v and u:
1f=1−1−1−∞
4. Simplify the Equation:
- Since 1−∞=0, the equation simplifies to:
1f=−1−0=−1
- Therefore, we find:
f=−1m
5. Calculate the Power of the Lens:
- The power P of a lens is given by the formula:
P=1f(in meters)
- Substitute f=−1m:
P=1−1=−1D
6. Conclusion:
- The power of the lens required to correct the man's eyesight so that he can see objects at infinity is −1D.
Final Answer:
The power of the lens required is −1D.
---
- The maximum distance at which the man can see clearly (near point) is d=1m.
- He wants to see objects at infinity, which means the object distance u=−∞ (the negative sign indicates that the object is on the same side as the incoming light).
- For the man to see an object at infinity, the image must be formed at his near point, which is v=−1m (again, the negative sign indicates that the image is formed on the same side as the object).
- The lens formula is given by:
1f=1v−1u
- Substitute the values of v and u:
1f=1−1−1−∞
- Since 1−∞=0, the equation simplifies to:
1f=−1−0=−1
- Therefore, we find:
f=−1m
- The power P of a lens is given by the formula:
P=1f(in meters)
- Substitute f=−1m:
P=1−1=−1D
- The power of the lens required to correct the man's eyesight so that he can see objects at infinity is −1D.
The power of the lens required is −1D.
Topper's Solved these Questions
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-1
1 Video
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - PRACTICE EXERCISE-2
1 Video
- RAY OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS EXERCISE - IN-CHAPTER EXERCISE-J
10 Videos
- QUIZBOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS
30 Videos
- RAY OPTICS AND WAVE OPTICS BOOK - VMC MODULES ENGLISHCHAPTER - RAY OPTICS AND WAVE OPTICS EXERCISE - IMPECCABLE
58 Videos
Similar Questions
Man can see objects equally clear from various distances due to
View SolutionA person cannot see beyond a distance of 50 cm.The power of corrective lens required to see distant object is
View SolutionA far sighted person cannot see object clearly al a distance less than 75 cm from his eyes. The power of the lens needed to read an object al 25 cm is
View SolutionA person suffering from defective vision can see objects clearly only beyond 100 cm from the eye. Find the power of lens required so that he can see clearly the object placed at a distance of distinct vision (D = 25cm)
View SolutionA person can see clearly objects only when they lie between 50 cm and 400 cm from his eyes. In order to increase the miximum distance of distinct vision to infinity , the person has to use, will be
View SolutionIf a person can sees clearly at a distance of 100 cm, then find the power of leris used to see object at 40 cm.
View SolutionIf the eye is kept very close to a coverging lens (focal length =10cm) and at the optical centre of the lens and an object is kept at distance 'd' of the object from the lebs so that its image can be seen clearly by the defect free eye is :
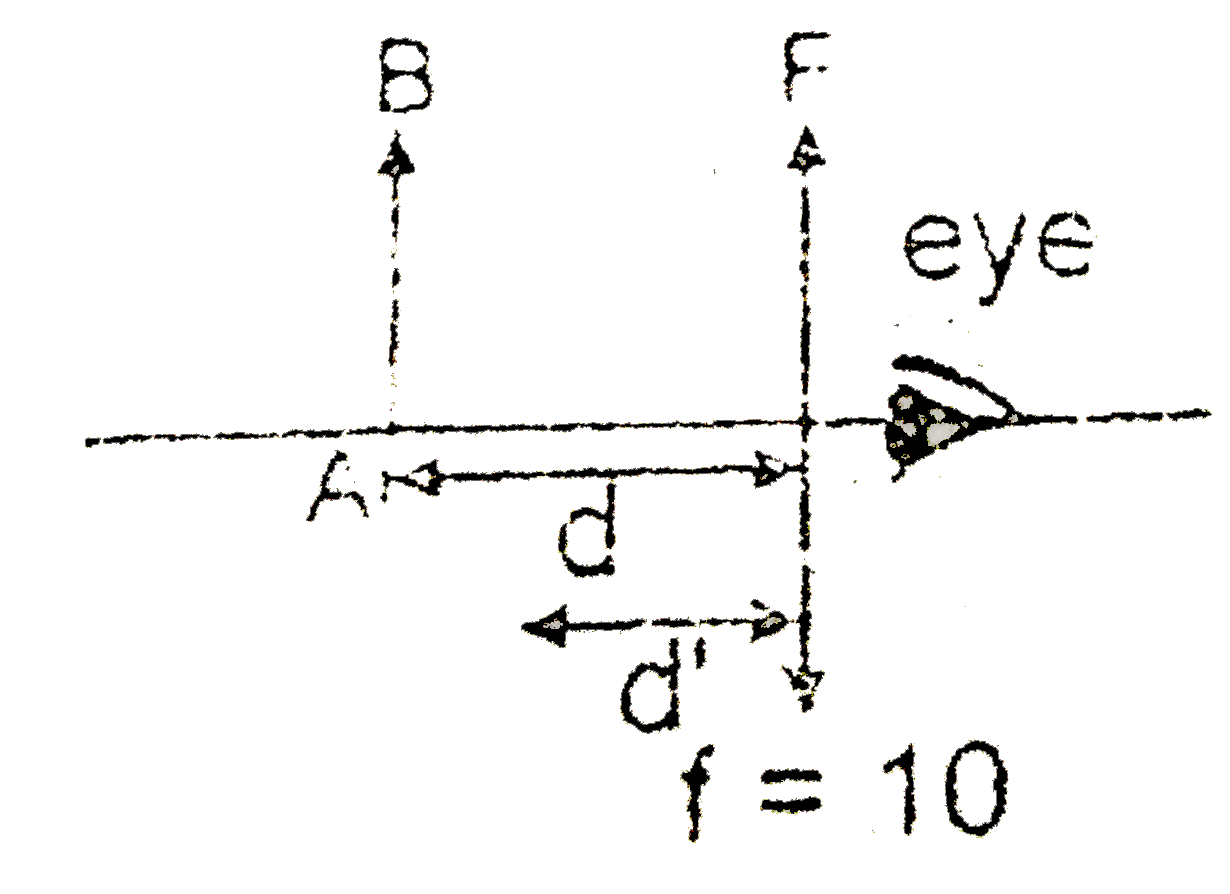 .
.
View SolutionIf the eye is kept very close to a coverging lens (focal length =10cm) and at the optical centre of the lens and an object is kept at distance 'd' of the object from the lebs so that its image can be seen clearly by the defect free eye is :
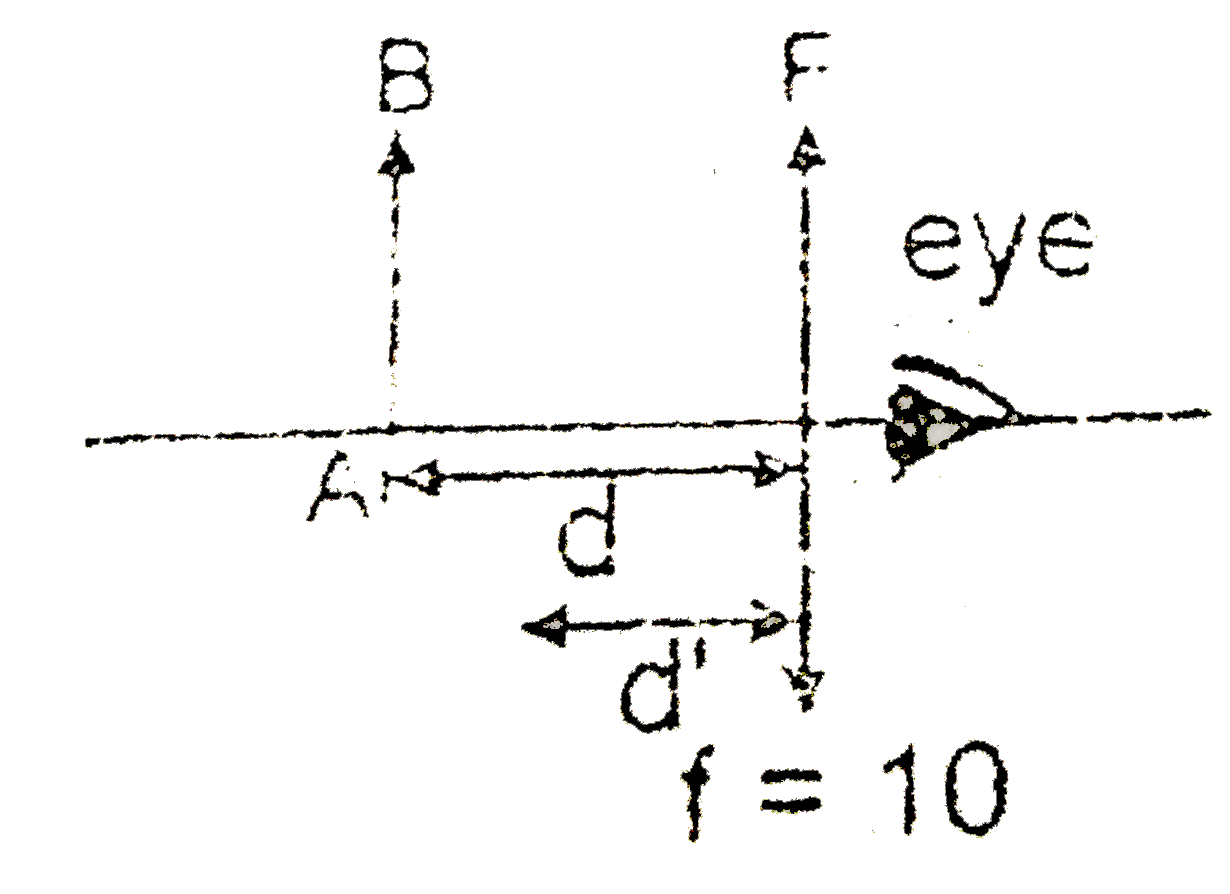 .
.
View SolutionA person cannot see objects clearly beyond 125 cm. The power of the lens to correct the vision is
View SolutionA person cannot see objects clearly beyond 50.cm. The power of lens to correct the vision
View Solution
