A block of mass 5 kg executes simple harmonic motion under the restoring force of a spring. The amplitude and the time period of the motion are 0.1 m and 3.14 s respectively. Find the maximum force exerted by the spring on the block.
To find the maximum force exerted by the spring on the block, we can follow these steps:
1. Identify Given Values:
- Mass of the block, m=5kg
- Amplitude of motion, A=0.1m
- Time period of motion, T=3.14s
2. Calculate Angular Frequency (ω):
The angular frequency ω can be calculated using the formula:
ω=2πT
Substituting the value of T:
ω=2π3.14≈2rad/s
3. Calculate Spring Constant (k):
The spring constant k can be calculated using the formula:
k=m⋅ω2
Substituting the values of m and ω:
k=5⋅(2)2=5⋅4=20N/m
4. Calculate Maximum Force (Fmax):
The maximum force exerted by the spring occurs when the block is at the extreme position (maximum displacement), which is equal to the amplitude A. The formula for the force exerted by the spring is:
Fmax=k⋅A
Substituting the values of k and A:
Fmax=20⋅0.1=2N
Final Answer:
The maximum force exerted by the spring on the block is 2N.
---
- Mass of the block, m=5kg
- Amplitude of motion, A=0.1m
- Time period of motion, T=3.14s
The angular frequency ω can be calculated using the formula:
ω=2πT
Substituting the value of T:
ω=2π3.14≈2rad/s
The spring constant k can be calculated using the formula:
k=m⋅ω2
Substituting the values of m and ω:
k=5⋅(2)2=5⋅4=20N/m
The maximum force exerted by the spring occurs when the block is at the extreme position (maximum displacement), which is equal to the amplitude A. The formula for the force exerted by the spring is:
Fmax=k⋅A
Substituting the values of k and A:
Fmax=20⋅0.1=2N
The maximum force exerted by the spring on the block is 2N.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective -1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
A body of mass 0.01 kg executes simple harmonic motion about x = 0 under the influence of a force as shown in figure. The time period of SHM is
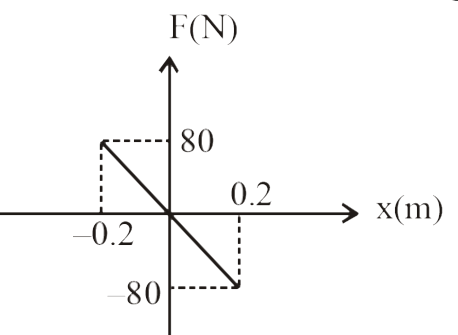
View SolutionA body of mass 0.01 kg executes simple harmonic motion (SHM) about x=0 under the influence of a force shown in the figure. The period of the SHM is
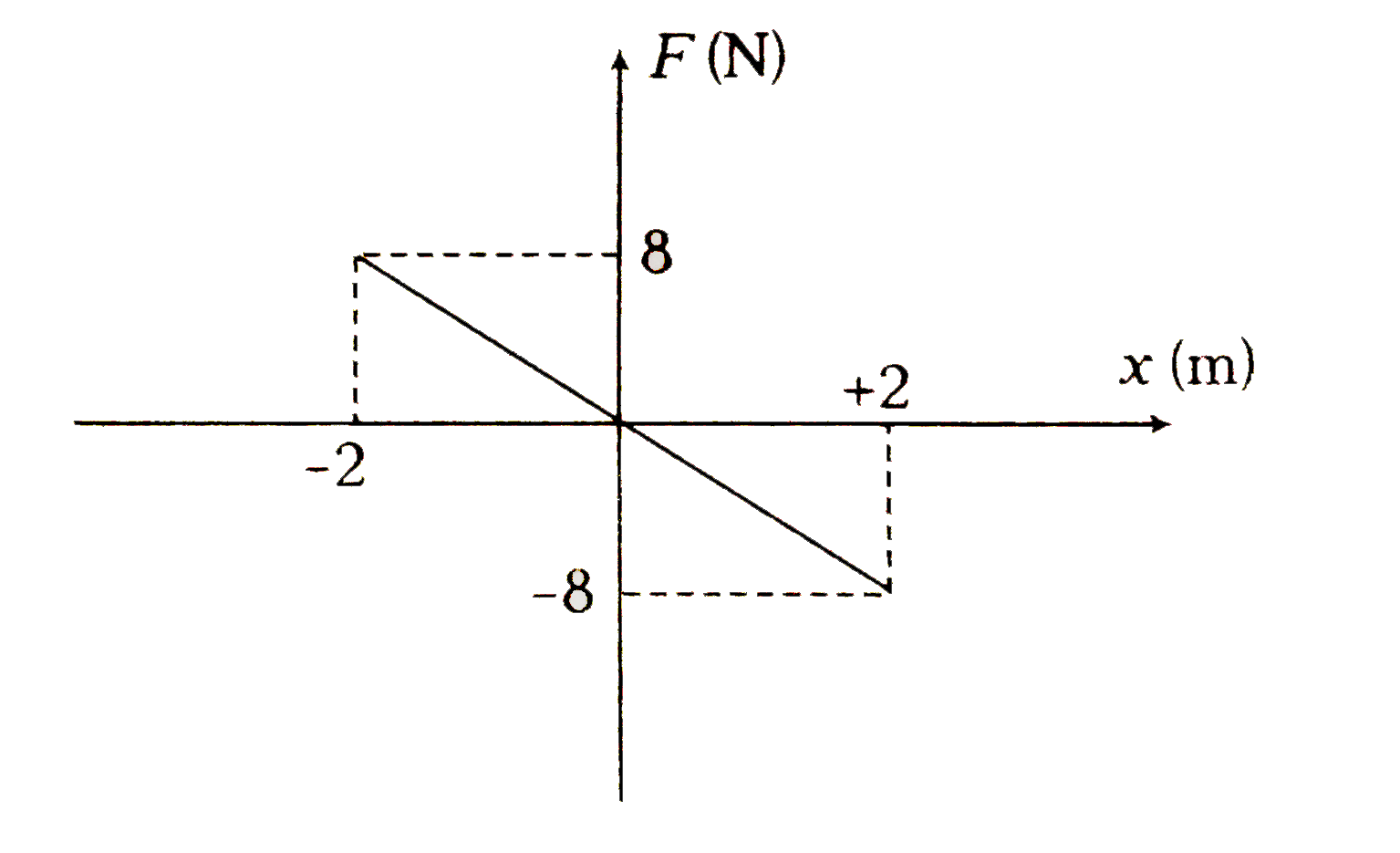
View SolutionA particle of mass 200g executes a simple harmonic motion. The restoring force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA paricle of mass 30kg executes a simple harmonic motion. The restorting force is provided by a spring of spring constant 80N/m. Find the time period.
View SolutionA block of mass 0.5 kg hanging from a vertical spring executes simple harmonic motion of amplitude 0.1 m and time period 0.314s. Find the maximum fore exerted by the spring on the blockl.
View SolutionA particle of mass 200 g executes a simpel harmonit motion. The resrtoring force is provided by a spring of spring constant 80Nm−1. Find the time period.
View SolutionA 5kg mass bounces in simple harmonic motion at the end of a spring. At which point the acceleration of the mass is the greatest?
View SolutionA particle executes simple harmonic motion under the restoring force provided by a spring. The time period is T. If the spring is divided in two equal parts and one part is used to continue the simple harmonic motion, the time period will
View SolutionA particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View SolutionA particle of mass 40 g executes a simple harmonic motion of amplitude 2.0 cm. If the time period is 0.20 s, find the total mechanical energy of the system.
View Solution
