A particle of mass 100 g moving at an initial speed u collides with another particle of same mass kept initially at rest. If the total kinetic energy becomes 0.2 J after the collision what could be minimum and the maximum value of u.
The correct Answer is:B
To solve the problem, we need to find the minimum and maximum values of the initial speed u of a particle of mass 100 g (0.1 kg) that collides with another particle of the same mass at rest, given that the total kinetic energy after the collision is 0.2 J.
1. Convert Mass to Kilograms:
The mass of each particle is given as 100 g. We convert this to kilograms:
m=100g=0.1kg
2. Write the Expression for Final Kinetic Energy:
The total kinetic energy after the collision is given as 0.2 J. The final kinetic energy can be expressed as:
KEf=12mV21+12mV22=0.2J
Substituting m=0.1kg:
0.1(12V21+12V22)=0.2
Simplifying gives:
V21+V22=4(Equation 1)
3. Apply Conservation of Momentum:
The initial momentum of the system is:
Pinitial=mu=0.1u
The final momentum is:
Pfinal=mV1+mV2=0.1V1+0.1V2
Setting the initial momentum equal to the final momentum:
0.1u=0.1(V1+V2)
This simplifies to:
u=V1+V2(Equation 2)
4. Relate Velocities Using Coefficient of Restitution:
The coefficient of restitution e relates the velocities before and after the collision:
e=V2−V1u
Rearranging gives:
V2−V1=eu(Equation 3)
5. Solve the System of Equations:
We have three equations:
- V1+V2=u (Equation 2)
- V21+V22=4 (Equation 1)
- V2−V1=eu (Equation 3)
From Equation 2, we can express V2 in terms of V1:
V2=u−V1
Substituting this into Equation 1:
V21+(u−V1)2=4
Expanding gives:
V21+(u2−2uV1+V21)=4
Simplifying:
2V21−2uV1+u2−4=0
This is a quadratic equation in V1.
6. Use the Discriminant:
For V1 to have real solutions, the discriminant must be non-negative:
D=(−2u)2−4⋅2⋅(u2−4)≥0
Simplifying:
4u2−8(u2−4)≥0
4u2−8u2+32≥0
−4u2+32≥0
u2≤8
Thus:
u≤√8=2√2
7. Find Minimum Value of u:
The minimum value of u occurs when e=1:
u=2(minimum)
8. Find Maximum Value of u:
The maximum value of u occurs when e=0:
u=2√2(maximum)
Final Answer
- Minimum value of u=2m/s
- Maximum value of u=2√2m/s
The mass of each particle is given as 100 g. We convert this to kilograms:
m=100g=0.1kg
The total kinetic energy after the collision is given as 0.2 J. The final kinetic energy can be expressed as:
KEf=12mV21+12mV22=0.2J
Substituting m=0.1kg:
0.1(12V21+12V22)=0.2
Simplifying gives:
V21+V22=4(Equation 1)
The initial momentum of the system is:
Pinitial=mu=0.1u
The final momentum is:
Pfinal=mV1+mV2=0.1V1+0.1V2
Setting the initial momentum equal to the final momentum:
0.1u=0.1(V1+V2)
This simplifies to:
u=V1+V2(Equation 2)
The coefficient of restitution e relates the velocities before and after the collision:
e=V2−V1u
Rearranging gives:
V2−V1=eu(Equation 3)
We have three equations:
- V1+V2=u (Equation 2)
- V21+V22=4 (Equation 1)
- V2−V1=eu (Equation 3)
V2=u−V1
Substituting this into Equation 1:
V21+(u−V1)2=4
Expanding gives:
V21+(u2−2uV1+V21)=4
Simplifying:
2V21−2uV1+u2−4=0
This is a quadratic equation in V1.
For V1 to have real solutions, the discriminant must be non-negative:
D=(−2u)2−4⋅2⋅(u2−4)≥0
Simplifying:
4u2−8(u2−4)≥0
4u2−8u2+32≥0
−4u2+32≥0
u2≤8
Thus:
u≤√8=2√2
The minimum value of u occurs when e=1:
u=2(minimum)
The maximum value of u occurs when e=0:
u=2√2(maximum)
- Minimum value of u=2m/s
- Maximum value of u=2√2m/s
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Question For short Answer
25 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -2
11 Videos
- CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONBOOK - HC VERMA ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM, COLLISIONEXERCISE - Objective -1
18 Videos
- CALORIMETRYBOOK - HC VERMA ENGLISHCHAPTER - CALORIMETRYEXERCISE - Short answer
9 Videos
- CIRCULAR MOTIONBOOK - HC VERMA ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Question for short Answer
10 Videos
Similar Questions
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
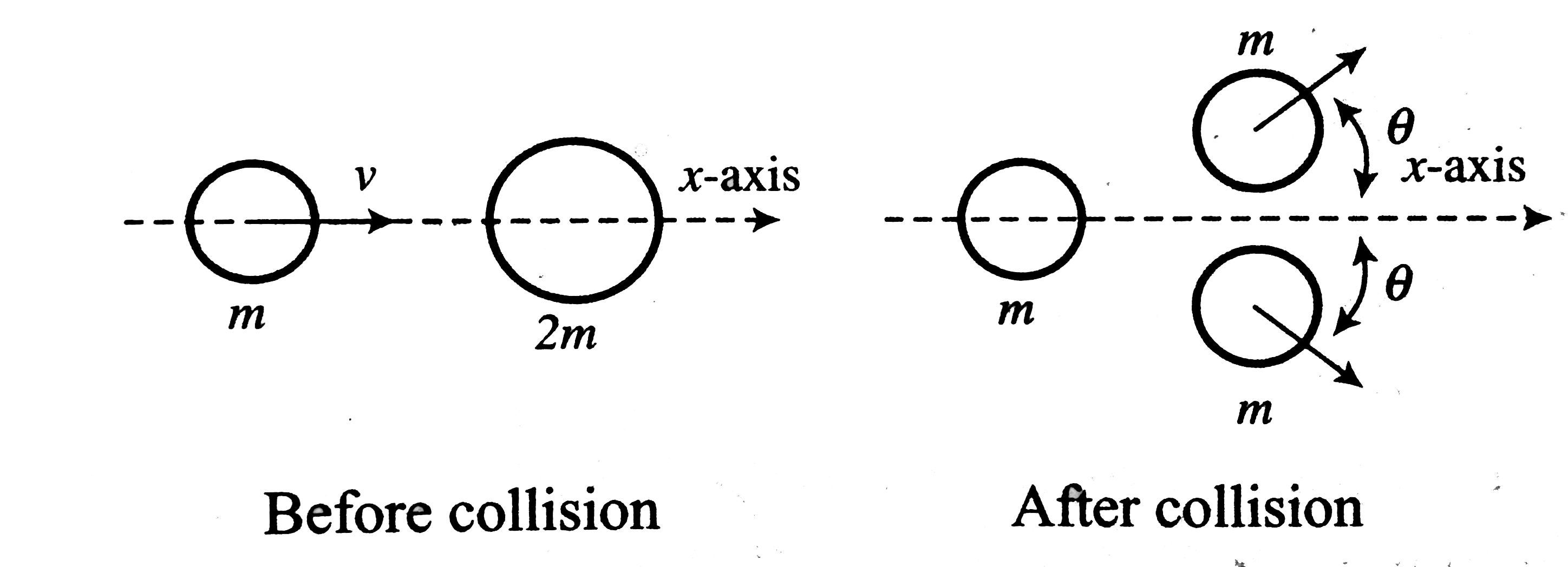
View SolutionA particle of mass m is moving along the x-axis with speed v when It collides with a particle of mass 2m initially at rest. After the collision, the first particle has come to rest and the second particle has split into two equal-mass pieces that are shown in the figure. Which of the following statements correctly describes the speeds of the two places? (θ>0)
View SolutionA moving particle of mass m makes a head-on perfectly inelastic collision with a particle of mas 2m which is initially at rest. Find the fractional loss in energy of the colliding partic le after collision.
View SolutionA body of mass m1 moving at a constant speed undergoes an elastic head on collision with a body of mass m2 initially at rest. The ratio of the kinetic energy of mass m1 after the collision to that before the collision is -
View SolutionIf one sphere collides head - on with another sphere of the same mass at rest inelastically. The ratio of their speeds (v2v1) after collision shall be
View SolutionOn a friction surface a block a mass M moving at speed v collides elastic with another block of same mass M which is initially at rest . After collision the first block moves at an angle θ to its initial direction and has a speed v3. The second block's speed after the collision is
View SolutionA body of mass 2 m moving with velocity v makes a head - on elastic collision with another body of mass m which is initially at rest. Loss of kinetic energy of the colliding body (mass 2 m) is
View Solution
