A body starts slipping down an incline and moves half meter in half second. How ling will it take to move the next half meter?
Supose the body is acceleratiing downward withan acceleration a
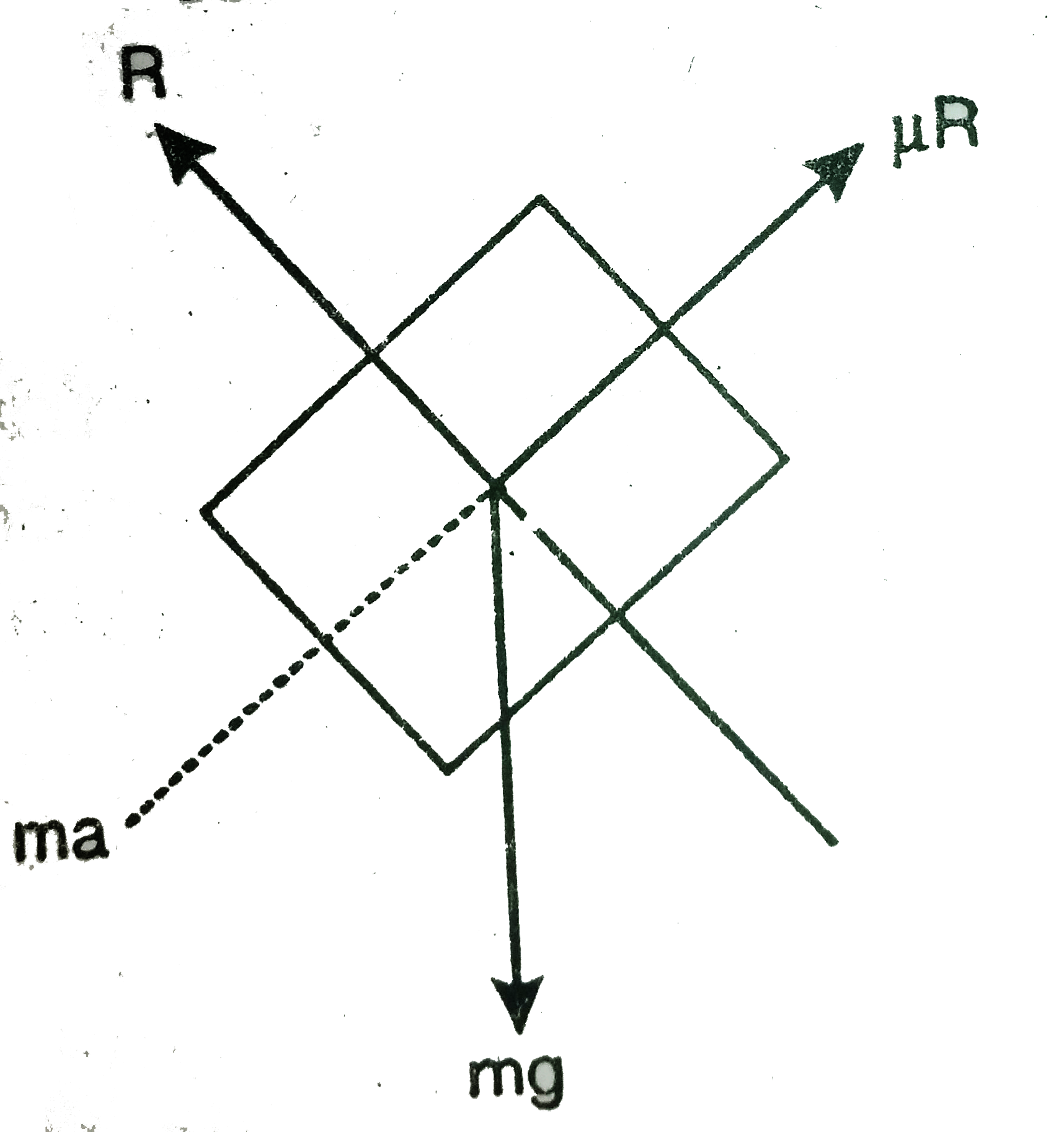
From the free body diagram
→R−mgcosθ=0
→R=mgcosθ…..i
and ma−mgsinθ−μR
=0
→a=mg(sinθ−μcosθ)m
=g(sinθ−μcosθ)
For the first halfmeter, <br>v=0<br>S=5m,t=0.5sec,<br>So,v=u+at<br>=0+(0.5)4=2m/sec
From S=ut+12at2
0.5=0+12a(0.5)2
→a=4ms2
For the next half metre
u=2msec,a=4ms2
S=0.5
→05=2t+(12)4t2
→2t2+2t−05=0
4t2+4t−1=0
→t=−4±√16+162×4<br>=1.656/8 = 0.2027
time taken to cover next that half meter is 0.21 sec.
Related Playlists
- BOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Questions for short Answer11videos
FRICTION
- BOOK - HC VERMA ENGLISHCHAPTER - FRICTIONEXERCISE - Objective -25videos
FRICTION
- BOOK - HC VERMA ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - All Questions90videos
FLUID MECHANICS
- BOOK - HC VERMA ENGLISHCHAPTER - GRAVITATIONEXERCISE - Question for short Answers18videos
GRAVITATION
Similar Questions
Hugo lies on top of a building, throwing pennies straight down to the street below. The formula for the height in meters, H, that a penny falls is H=Vt+5t2, where V is the original velocity of the penny (how fast Hugo throws it as it leaves his hand in meters per second) and t is equal to the time it takes to hit the ground in seconds. The building is 60 meters high, and Hugo throws the penny down at an initial speed of 20 meters per second. How long does it take for the penny to hit the ground?
View SolutionA body dropped from top of a tower falls through 40m during the last two seconds of its fall. The height of tower in m is ( g= 10 m//s^2)
View SolutionThe half life of a first order reaction is 60min. How long will is take to consume 90% of the reactant?
View SolutionA body starts from rest and moves with a uniform acceleration of 10ms−2 for 5 seconds. During the next 10 seconds it moves with uniform velocity. Find the total distance travelled by the body (Using graphical analysis).
View SolutionA body starts from rest and moves with a uniform acceleration of 10ms−2 for 5 seconds. During the next 10 seconds it moves with uniform velocity. Find the total distance travelled by the body (Using graphical analysis).
View SolutionStarting from rest , a body slides down at 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of friction between the body and the inclined plane is
View SolutionStarting from rest a body slides down a 45∘ inclined plane in twice the time it takes to slide down the same distance in the absence of friction. The coefficient of the body and the inclined plane is :
View SolutionA body is moving down along inclined plane of angle of inclination q. The coefficient of friction between the body and the plane varies as mu = 0.5x, where x is the distance moved down the plane. The body will have the maximum velocity when it has travelled a distance x given by
View SolutionA particle starts moving from position of rest under a constant acceleration. If it travels a distance x in t second, what distance will it travel in next t second?
View SolutionA cylindrical water tank has a diameter of 14 meters and a height of 20 meters. A water truck can fill π cubic meters of the tank every minute. How long will take the water truck to fill water tank from empty to half full?
View Solution


