An elevator is descending with uniform acceleration.To measure the acceleration, a person in the elevator drops a coin at momen the elevator strts. The coin is 6 ft asbove the floor of the elevator at the time it is dropped. The person observes that the coin strikes the floor in 1 second. Calculate these dta the acceleration of the elevator.
To solve the problem, we need to determine the acceleration of the elevator based on the motion of the coin dropped from it. Here’s a step-by-step solution:
Step 1: Understand the Problem
The elevator is descending with uniform acceleration, and a coin is dropped from a height of 6 feet above the floor of the elevator. The coin strikes the floor of the elevator in 1 second. We need to find the acceleration of the elevator.
Step 2: Define Variables
- Let A be the acceleration of the elevator (in feet per second squared).
- The acceleration due to gravity g is approximately 32ft/s2.
- The distance sc that the coin travels is 6ft.
- The time t taken for the coin to hit the floor is 1s.
Step 3: Establish the Equation of Motion
When the coin is dropped, it has an initial velocity u=0 (since it is dropped). The effective acceleration of the coin relative to the elevator is g−A, where g is the acceleration due to gravity and A is the acceleration of the elevator.
Using the equation of motion:
sc=ut+12a′t2
where a′=g−A.
Substituting the known values:
6=0⋅1+12(g−A)(12)
This simplifies to:
6=12(g−A)
Step 4: Substitute the Value of g
Substituting g=32ft/s2 into the equation:
6=12(32−A)
Step 5: Solve for A
Multiply both sides by 2 to eliminate the fraction:
12=32−A
Rearranging gives:
A=32−12
A=20ft/s2
Conclusion
The acceleration of the elevator is 20ft/s2.
The elevator is descending with uniform acceleration, and a coin is dropped from a height of 6 feet above the floor of the elevator. The coin strikes the floor of the elevator in 1 second. We need to find the acceleration of the elevator.
- Let A be the acceleration of the elevator (in feet per second squared).
- The acceleration due to gravity g is approximately 32ft/s2.
- The distance sc that the coin travels is 6ft.
- The time t taken for the coin to hit the floor is 1s.
When the coin is dropped, it has an initial velocity u=0 (since it is dropped). The effective acceleration of the coin relative to the elevator is g−A, where g is the acceleration due to gravity and A is the acceleration of the elevator.
sc=ut+12a′t2
where a′=g−A.
6=0⋅1+12(g−A)(12)
This simplifies to:
6=12(g−A)
Substituting g=32ft/s2 into the equation:
6=12(32−A)
Multiply both sides by 2 to eliminate the fraction:
12=32−A
Rearranging gives:
A=32−12
A=20ft/s2
The acceleration of the elevator is 20ft/s2.
Topper's Solved these Questions
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Question for short Answer
Explore 13 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Objective -2
Explore 9 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMA ENGLISHChapter:PHYSICS AND MATHEMATICSExercise:Question for short Answer
Explore 14 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
Similar Questions
An elevator (lift) ascends with an upward acceleration of 1.2ms−2. At the instant when its upward speed is 2.4ms−1, a loose bolt drops from the ceiling of the elevator 2.7m above the floor of the elevator. Calculate (a) the time of flight of the bolt from the ceiling to the floor and (b) the distance it has fallen relaative to the elevator shaft.
View SolutionA person standing oin the floor of an elevator drops as coin. The coin reaches the floor of the elevator in a time t1 if the elevator is stationary and in the t2 if it is moving uniformly. Then
View SolutionThe force exerted by the floor of an elevator on the foot of a person standing there is more than the weight of the person if the elevator is :
View SolutionAn elevator is moving vertically up with a acceleration a the force exerted on the floor by a passenger of mass m is
View Solution
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the acceleration of the elevator in upward direction, (mss2):
View SolutionA train is moving forward with a horizontal acceleration a. A man sitting in the train drops a coin on the floor of the train . The acceleration of the coin w.r.t man is
View SolutionAn elevator of height 'h' ascends with constant acceleration 'a'. When it corsses a plalform bolt drops from the top of the elevator. If the time for the bolt to hit the floor of the elevator is √λhg+a then find 'λ'.
View SolutionConsider an elevator moving downwards with an acceleration a, the force exerted by a passenger of mass m on the floor of the elevator is :
View Solution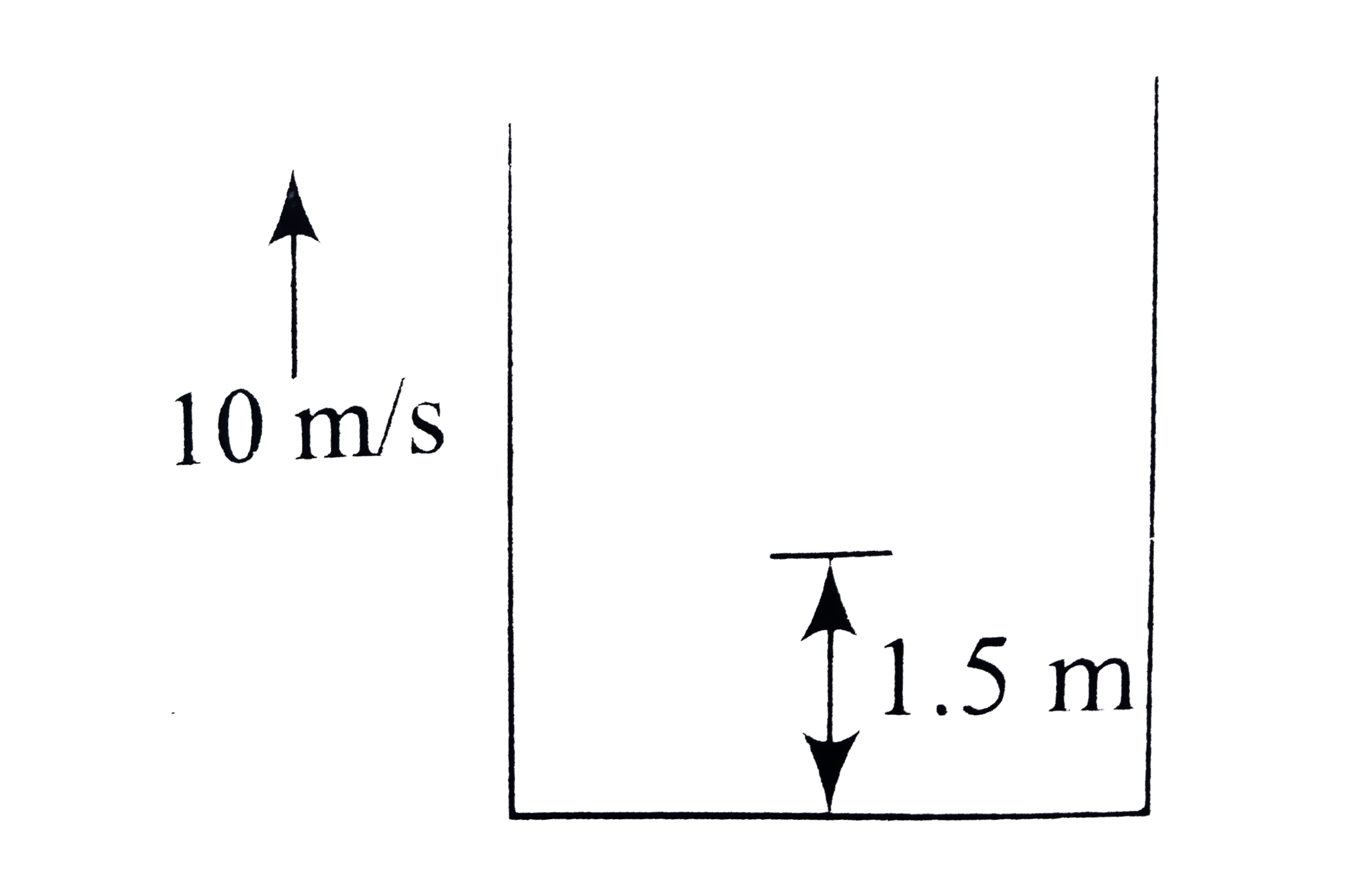
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :
View Solution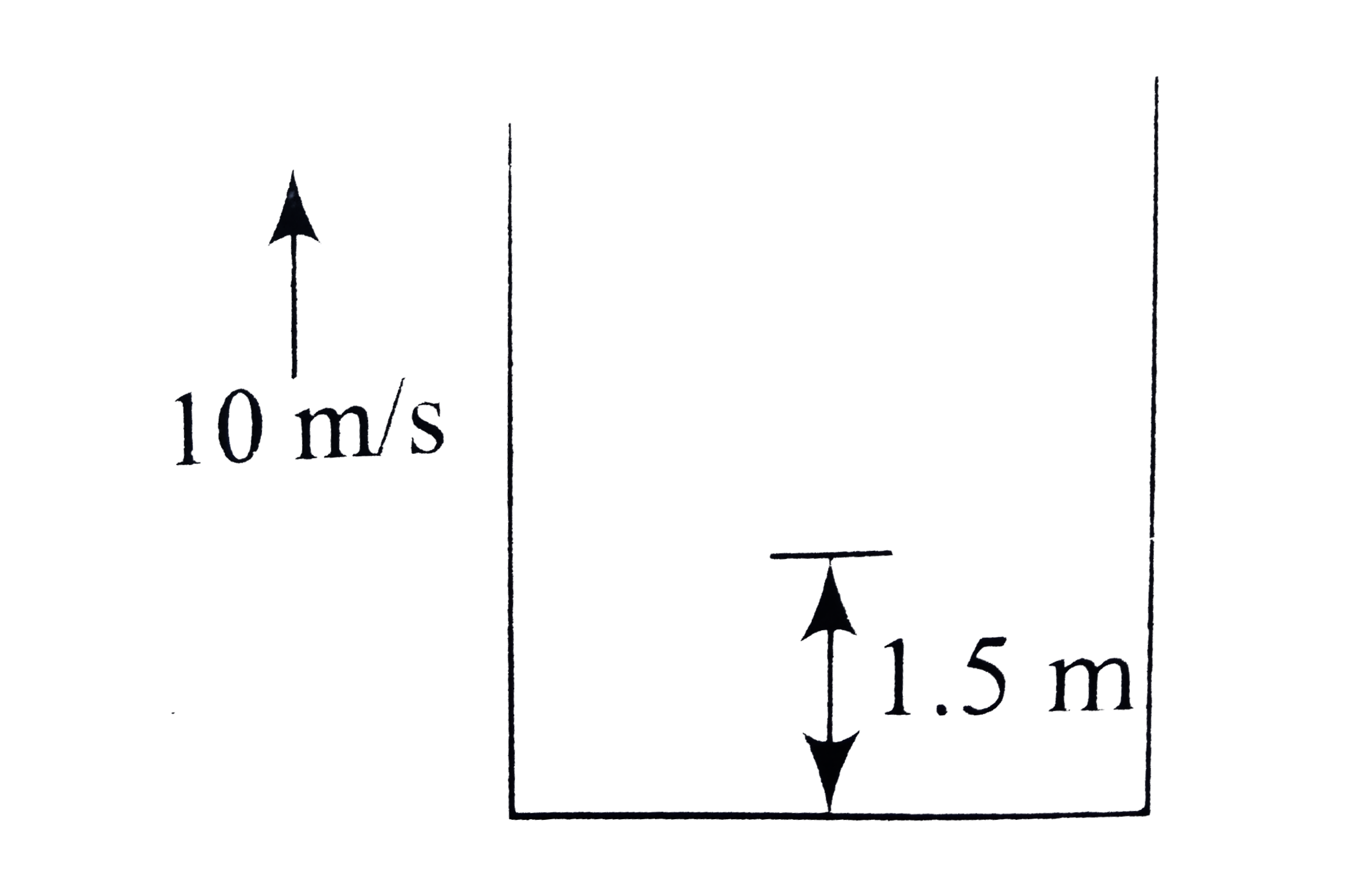
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the displacement of the bullet relative to ground during its flight:
View Solution