The sum of the three vectors shown in figure is zero. Find the magnitudes of the vectors . 
Take the axes as shown in the ure

The x-component of
The x-component of vec(OC)=(OC) cos 135^0= - 1/sqrt(2) OC. OB- 1/sqrt2 OC.OB 1/sqrt2 OCThe y-component of
The y-component of .
The y-component of .
.....iii
As the resultant is zero so is its y-compoentn from iii,
From i. .
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBook:HC VERMA ENGLISHChapter:PHYSICS AND MATHEMATICSExercise:Objective 1
Explore 6 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMA ENGLISHChapter:PHYSICS AND MATHEMATICSExercise:Objective 2
Explore 5 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMA ENGLISHChapter:PHYSICS AND MATHEMATICSExercise:Question for short Answer
Explore 14 Videos
- NEWTON'S LAWS OF MOTIONBook:HC VERMA ENGLISHChapter:NEWTON'S LAWS OF MOTIONExercise:Questions for short Answer
Explore 17 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Question for short Answer
Explore 13 Videos
Similar Questions
The sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
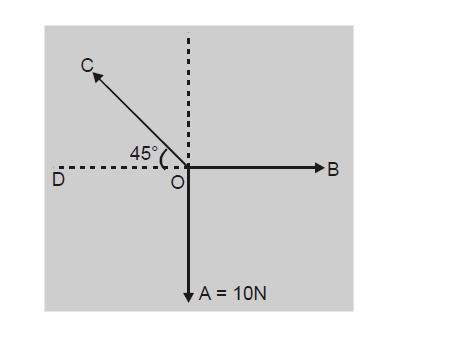
(ii) What is the magnitude of vector −−→OC ?
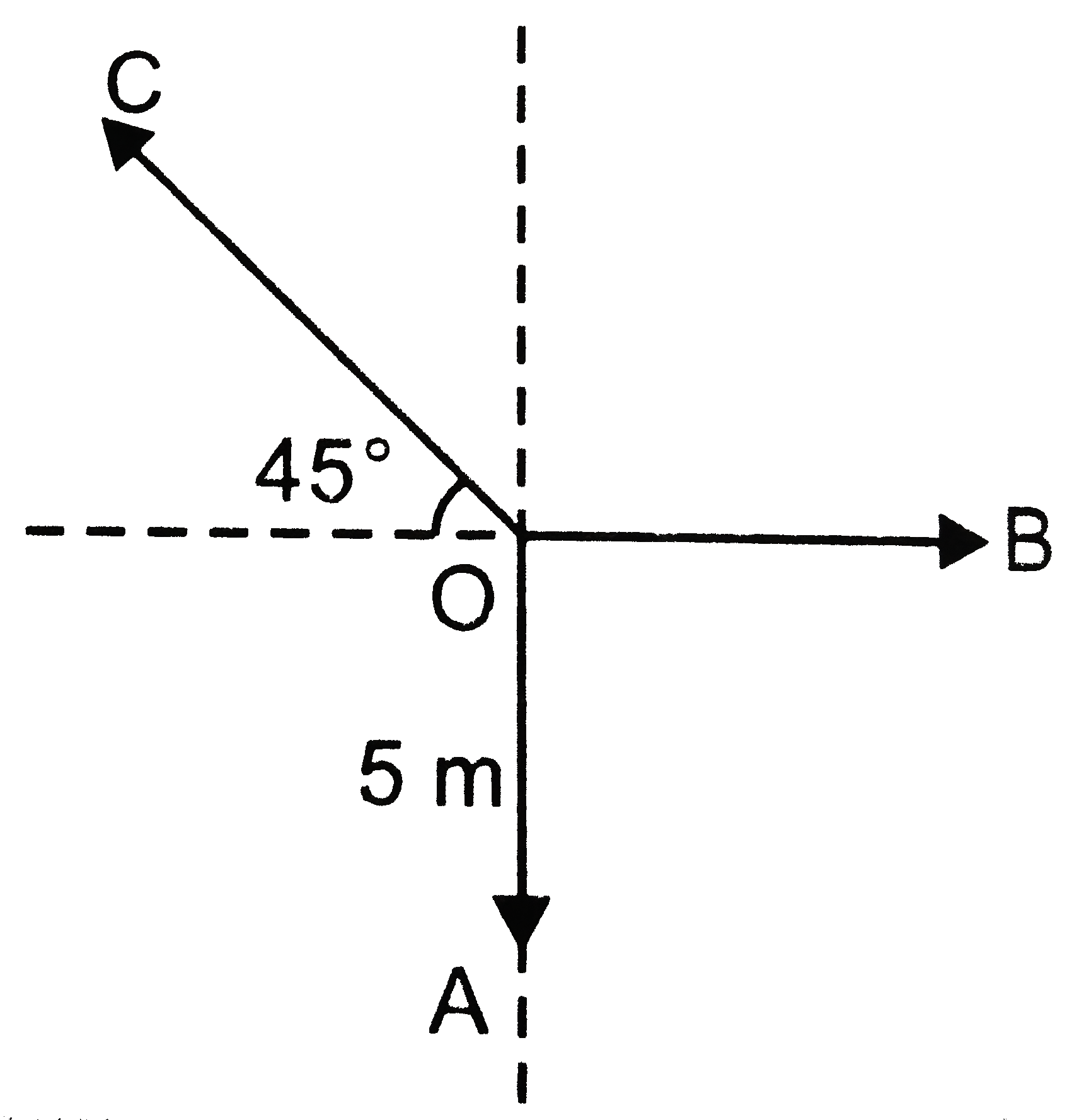
View SolutionThe sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
 .
.
(a) What is the magnitude of the vector −−→OB?
(b) What is the magnitude of the vector −−→OC ?
View Solution
Knowledge Check
The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
A3B4C5D8
A vector →A of length 10 units makes an angle of 60∘ with a vector →B of length 6 units. Find the magnitude of the vector difference →A−→B & the angles with vector →A.
View SolutionIf →A→B,→C are three vectors and one of them has zero magnitude , then given that →A×→B=0and→B×→C=0 , Prove that →A×→c=0
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
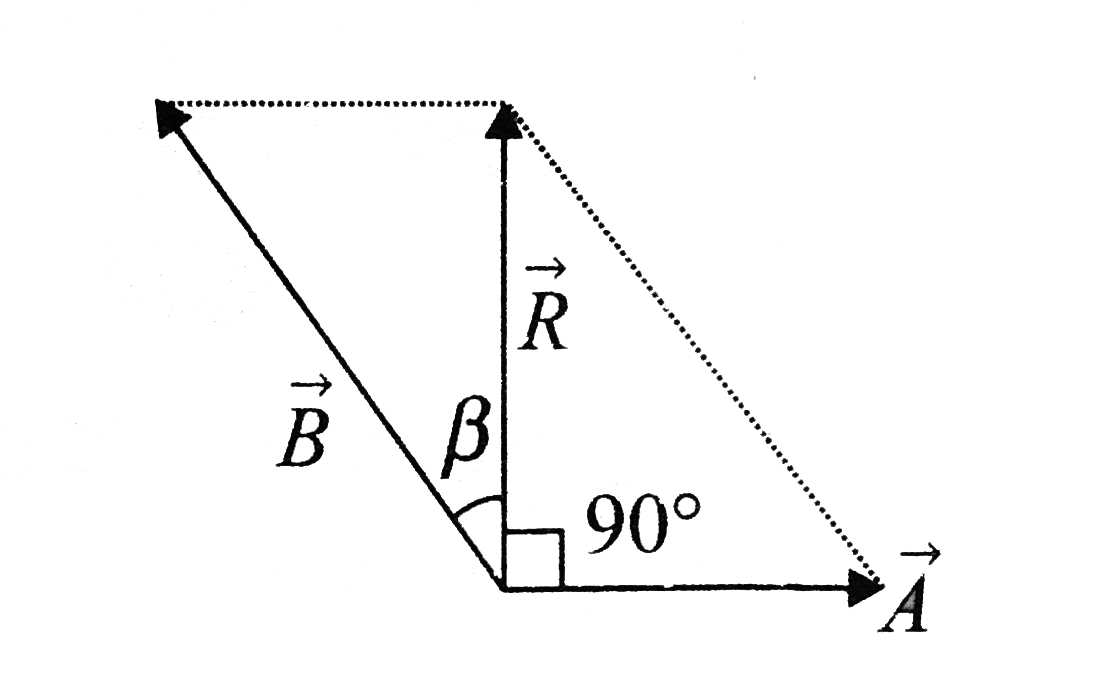
View SolutionGiven that →A+→B+→C=→0. Out of three vectors, two are equal in magnitude and the magnitude of the third vectors is √2 times that of either of the two having equal magnitude. Find the angles between the vectors.
View SolutionGiven that →A+→B+→C=→0. Out of three vectors,two are equal in magnitude and the magnitude of the third vectors is √2 times that of either of the two having equal magnitude. Find the angles between the vectors.
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionFind the resultant of the three vectors −−→OA,−−→OB and −−→OC shown in figure. Radius of the circle is R.

View Solution

