The resultant of vectors −−→OAand−−→OB is perpendicular to −−→OA. Find the angle AOB.
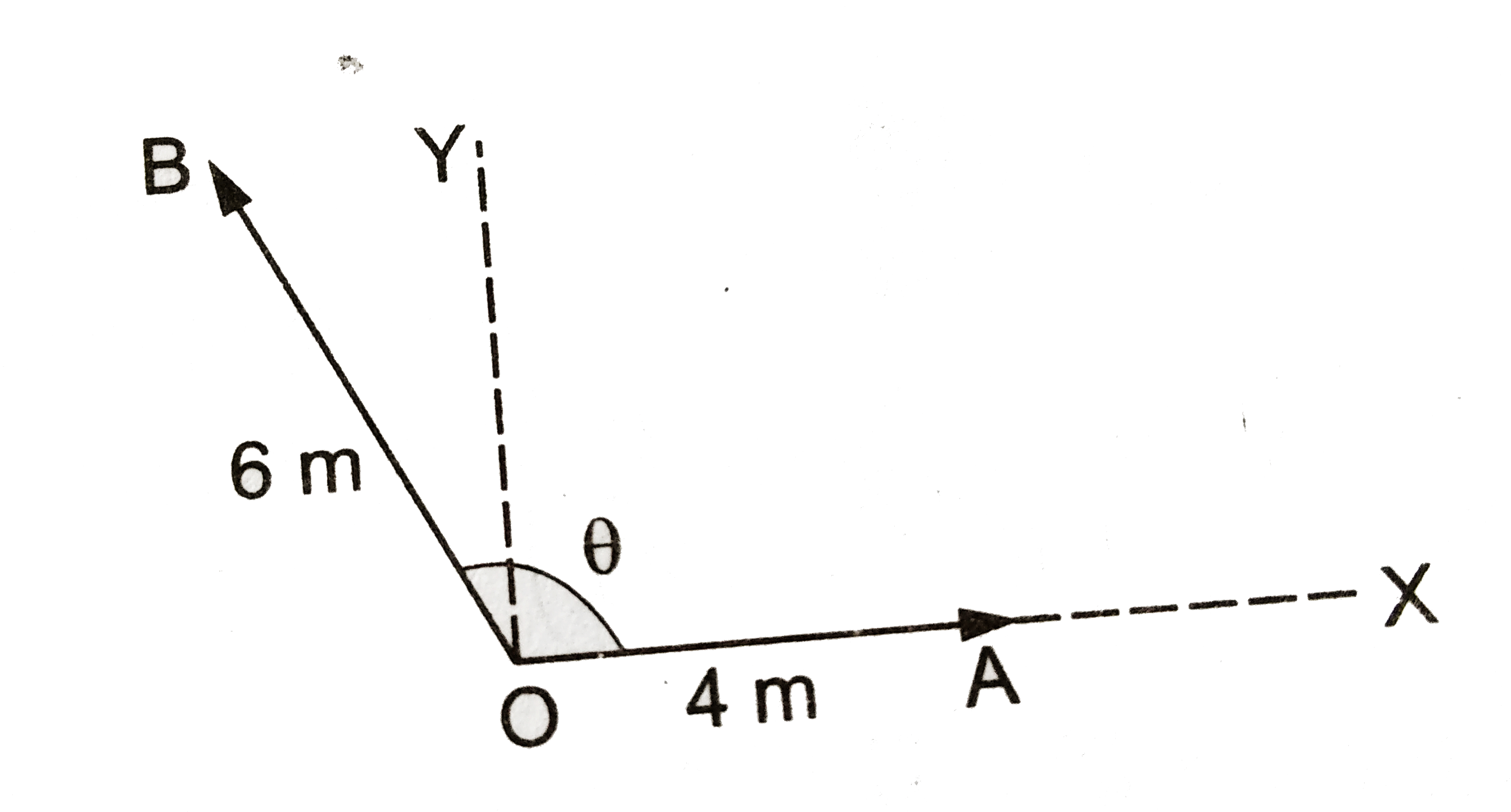
Take the dotted lines as X,Y axes.
x -component of −−→OA=4m, x-component of
−−→OB=6mcosθ.
x- component of the resultant =(4+6cosθ) m.
But it is given that the resultant is along Y-axis. Thus, the -component of the resultant =0
4+6cosθ=0,or,cosθ=23
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Objective 1
6 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Objective 2
5 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer
17 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
Similar Questions
The resultant of vectors −−→OAand−−→OB is peerpendicular to −−→OA. Find the angle AOB.

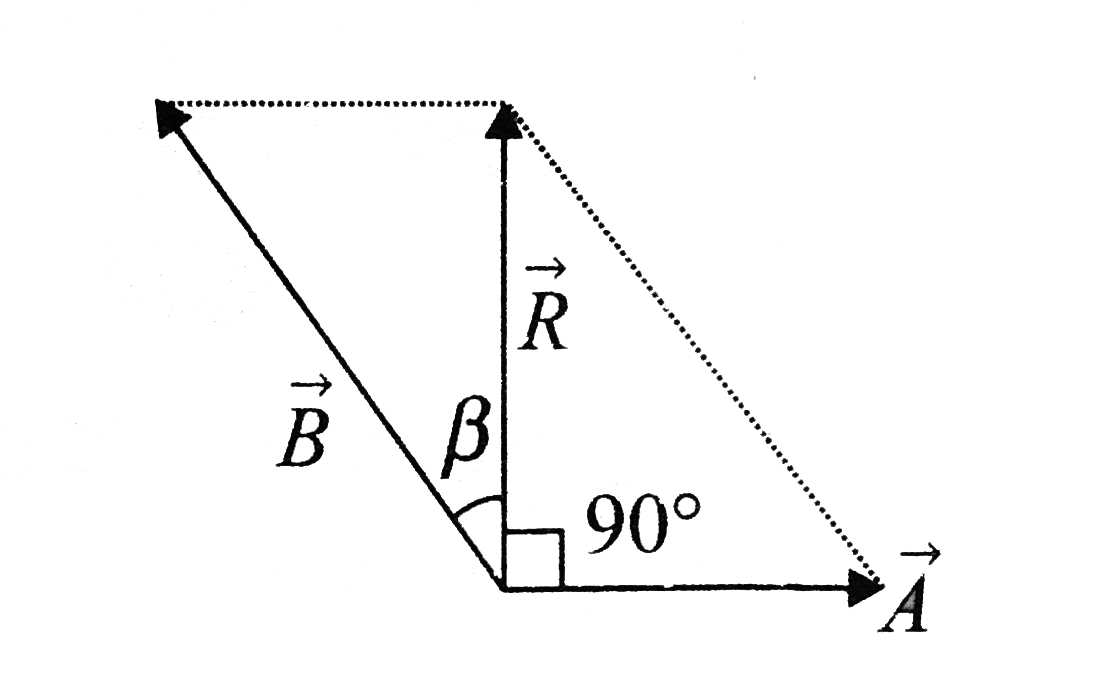
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
View SolutionThe resultant →Pand→Q is perpendicular to →P. What is the angle between →Pand→Q?
View SolutionThe resultant of two vectors →P and →Q is →R. If →Q is doubled then the new resultant vector is perpendicular to →P. Then magnitude of →R is :-
View SolutionTwo vectors →P and →Q are added, the magnitude of resultant is 15 units. If →Q is reversed and added to →P resultant has a magnitude √113 units. The resultant of →P and a vector perpendicular →P and equal in magnitude to→Q has a magnitude
View SolutionIf →A,→B&→A+→B are three non− zero vector. Such that →A+→B is perpendicular to →B then which of one is correct :
View SolutionLet →a,→b,and→c are vectors such that |→a|=3,∣∣→b∣∣=4and|→c|=5,and(→a+→b) is perpendicular to →c,(→b+→c) is perpendicular to →aand(→c+→a) is perpendicular to →b. Then find the value of ∣∣→a+→b+→c∣∣ .
View SolutionThe resultant and dot product of two vectors →aand→b is equal to the magnitude of →a. Show that when the vector →a is doubled , the new resultant is perpendicular to →b .
View SolutionThe magnitude of vectors −−→OA,−−→OBand−−→OC in figure are equal. Find the direction of −−→OA+−−→OB−−−→OC.
 .
.
View SolutionThe vector (→a+3→b) is perpendicular to (7→a−5→b) and (→a−4→b) is perpendicular to (7→a−2→b). The angle between →a and →b is :
View Solution
