The velocity v and displacement x of a particle executing simple harmonic motion are related as
vdvdx=−ω2x.
Atx=0,v=v0. Find the velocity v when the displacement becomes x.
To solve the problem, we start with the given relationship between velocity v and displacement x for a particle executing simple harmonic motion:
vdvdx=−ω2x
Step 1: Rearranging the Equation
We can rearrange the equation to separate variables. This gives us:
vdv=−ω2xdx
Step 2: Integrating Both Sides
Next, we will integrate both sides. The left side is integrated with respect to v and the right side with respect to x:
∫vdv=∫−ω2xdx
Step 3: Performing the Integrations
The left side integrates to:
v22+C1
And the right side integrates to:
−ω2x22+C2
Combining these results, we have:
v22=−ω2x22+C
where C=C2−C1.
Step 4: Applying Initial Conditions
We know that at x=0, v=v0. Plugging these values into our equation gives:
v202=−ω2(0)22+C
This simplifies to:
C=v202
Step 5: Substituting Back into the Equation
Now we substitute C back into our integrated equation:
v22=−ω2x22+v202
Step 6: Solving for v2
Multiplying through by 2 to eliminate the fraction gives:
v2=v20−ω2x2
Step 7: Taking the Square Root
Finally, we take the square root to find v:
v=√v20−ω2x2
This is the expression for the velocity v when the displacement is x.
Final Answer
v=√v20−ω2x2
---
We can rearrange the equation to separate variables. This gives us:
Next, we will integrate both sides. The left side is integrated with respect to v and the right side with respect to x:
The left side integrates to:
We know that at x=0, v=v0. Plugging these values into our equation gives:
Now we substitute C back into our integrated equation:
Multiplying through by 2 to eliminate the fraction gives:
Finally, we take the square root to find v:
v=√v20−ω2x2
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBook:HC VERMA ENGLISHChapter:PHYSICS AND MATHEMATICSExercise:Objective 1
Explore 6 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMA ENGLISHChapter:PHYSICS AND MATHEMATICSExercise:Objective 2
Explore 5 Videos
- PHYSICS AND MATHEMATICSBook:HC VERMA ENGLISHChapter:PHYSICS AND MATHEMATICSExercise:Question for short Answer
Explore 14 Videos
- NEWTON'S LAWS OF MOTIONBook:HC VERMA ENGLISHChapter:NEWTON'S LAWS OF MOTIONExercise:Questions for short Answer
Explore 17 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Question for short Answer
Explore 13 Videos
Similar Questions
Knowledge Check
A particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2Which of the following relationships between the acceleration a and the displacement x of a particle executing simple harmonic motion?
Aa=2x2Ba=−2x2Ca=2xDa=−2x
The acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View SolutionObtain the formulae for displacement, velocity, acceleration and time period of a particle executing simple harmonic motion. When is the velocity of particle maximum and when zero ? Acceleration ?
View SolutionThe acceleration (a) of a particle depends on displacement (s) as a=5+s . Initially s=0,v=5, then velocity v corresponding to the displacement is given by
View SolutionIf a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
View SolutionFor a particle undergoing simple harmonic motion, the velocity is plotted against displacement. The curve will be
View SolutionThe velocity-displacement graph of a particle is shown in Fig . (a) Write the relation between (v) and (x).
(b) Obtain the relation between acceleration and displacement and plot it .
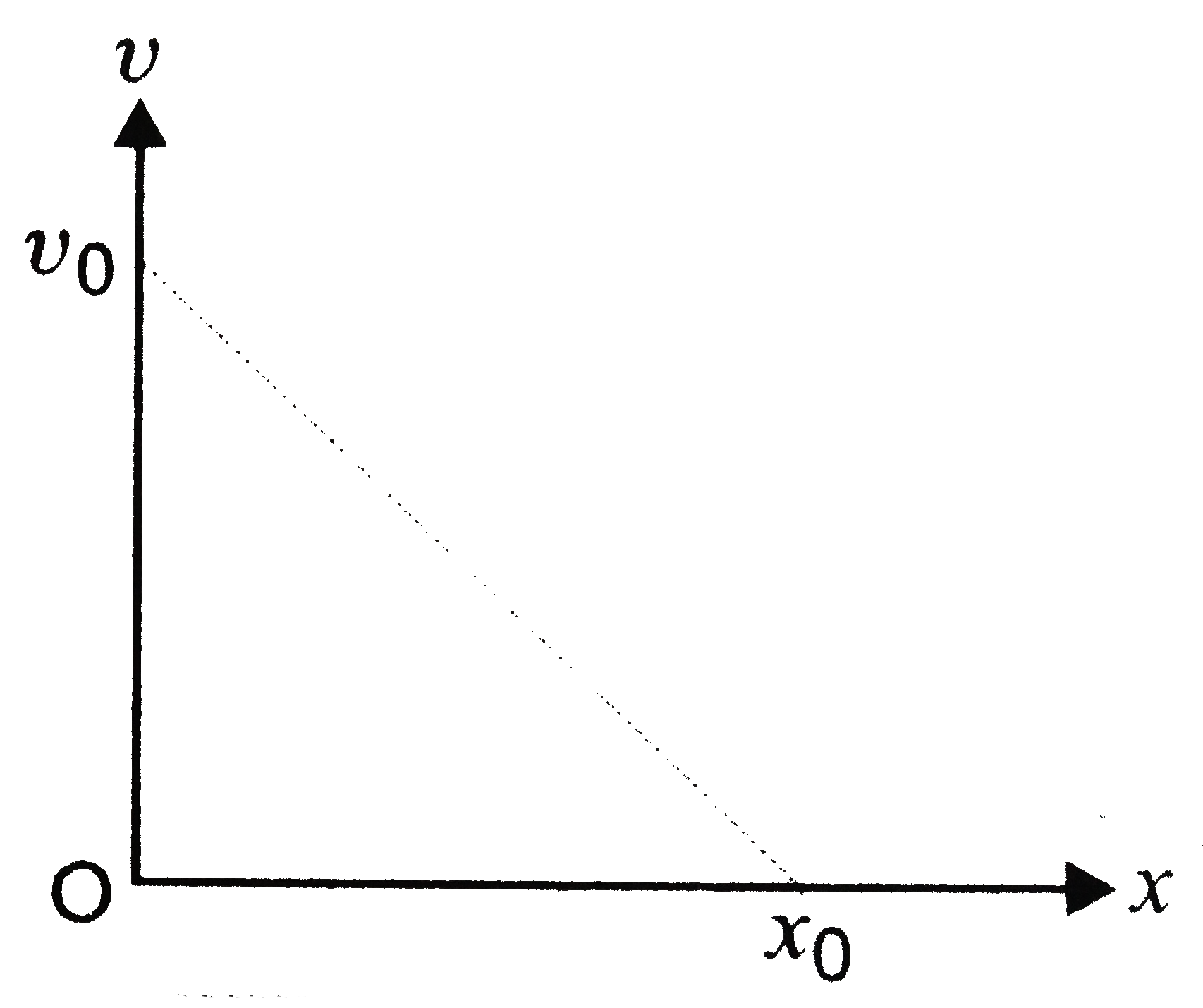 .
.
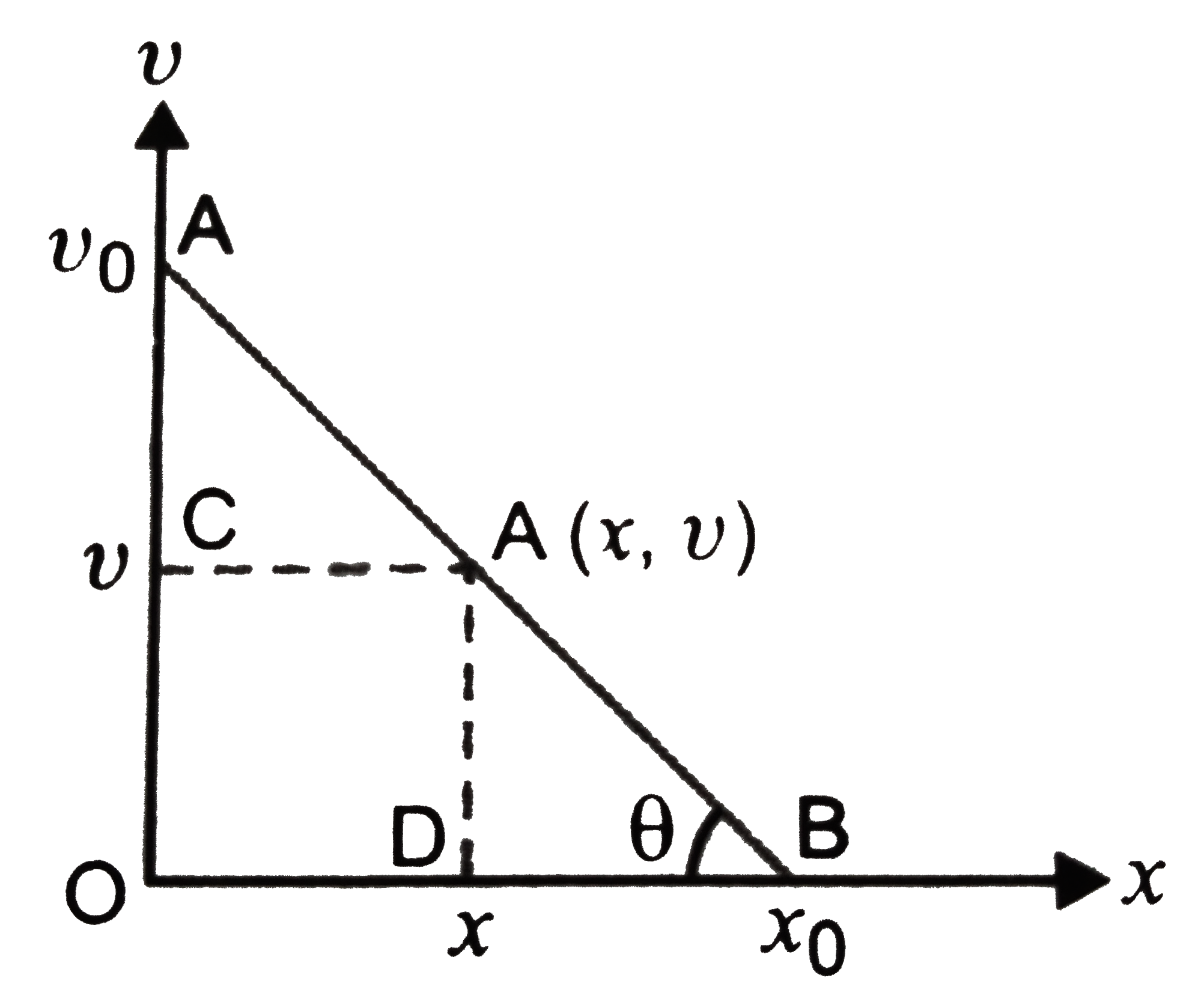 .
.
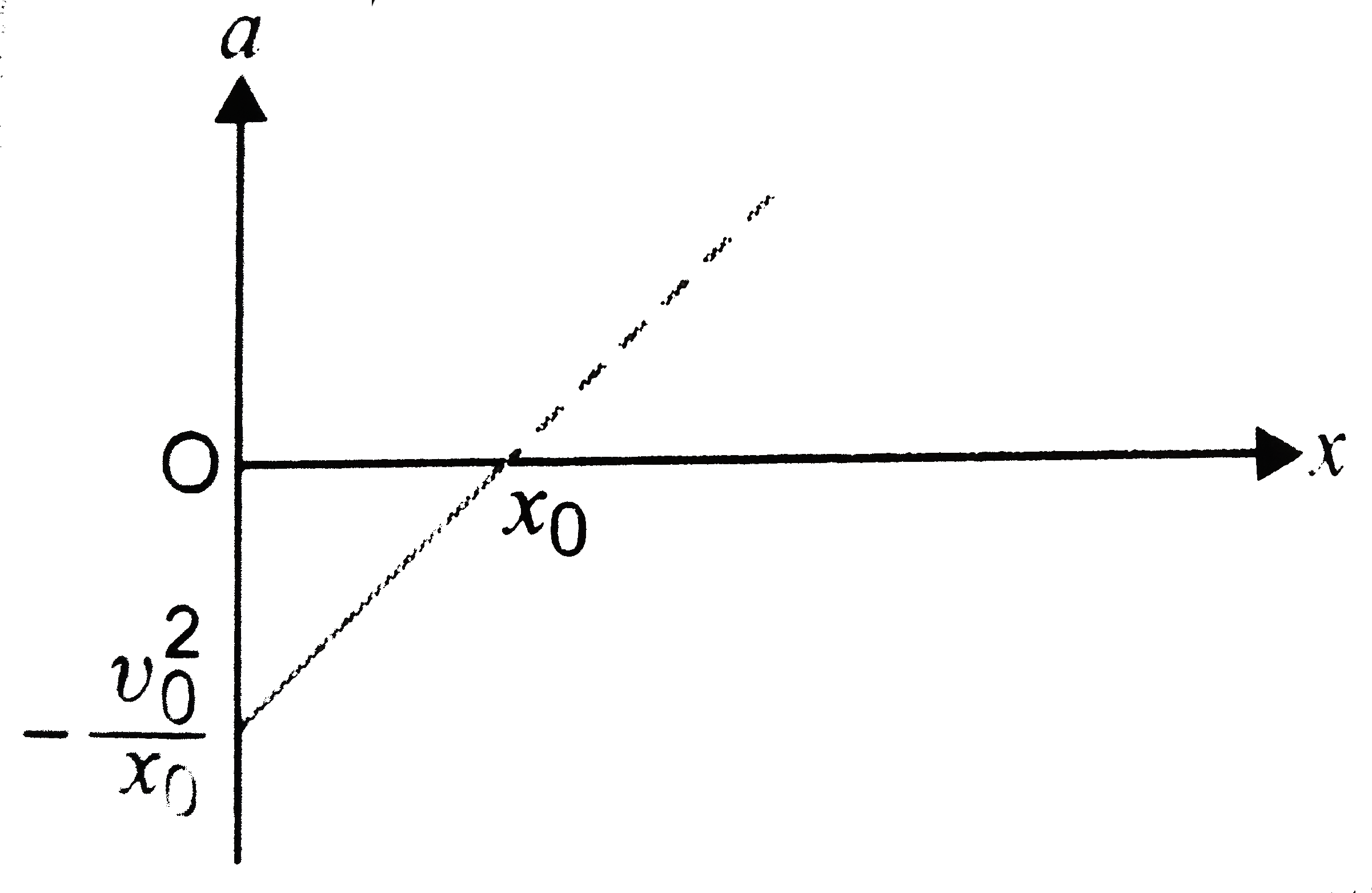 .
.
View Solution


