In the given figue vertices of lie on . The is right angled isosceles triangle whose hypotenuse units.
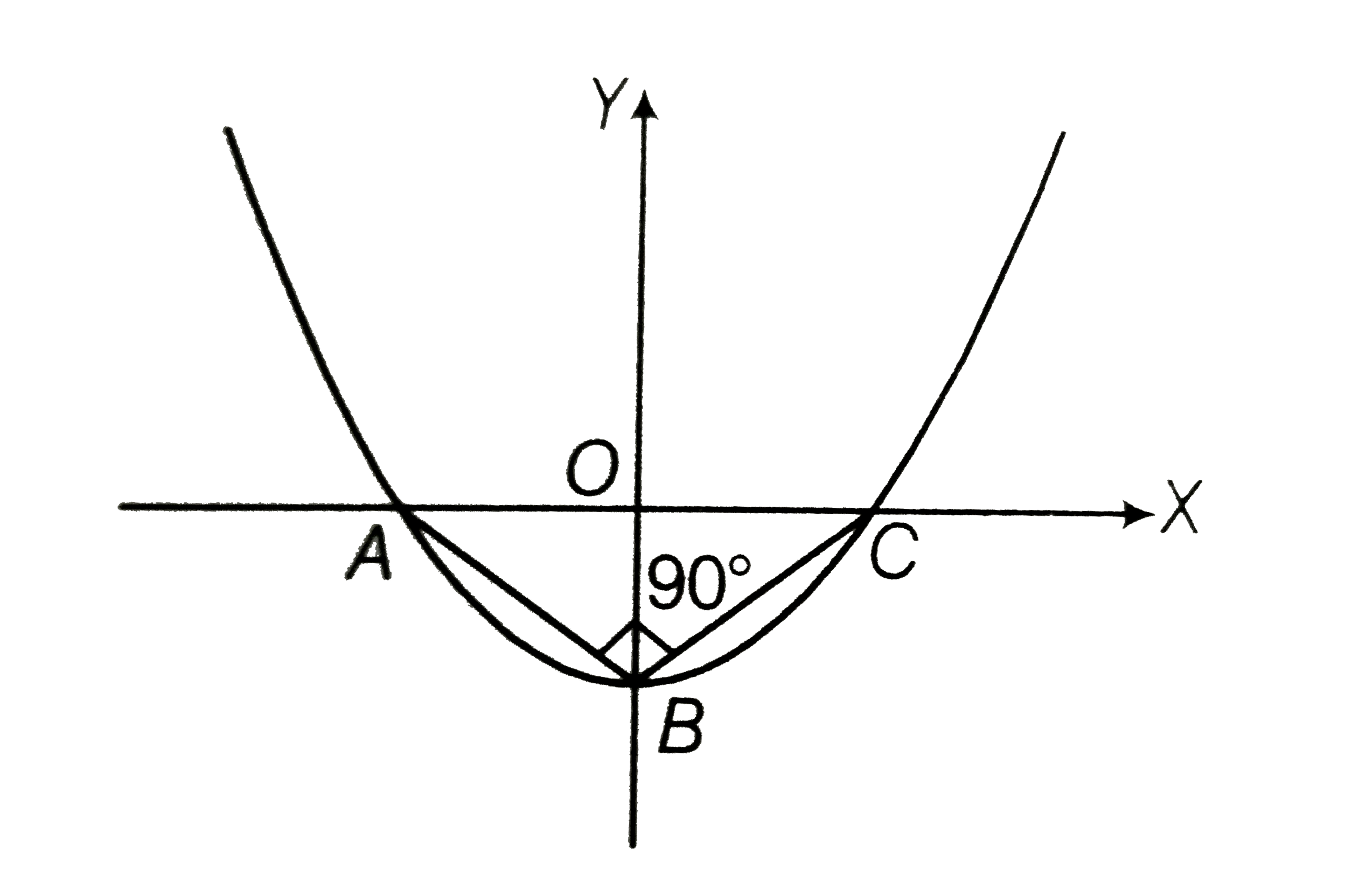
Number of integral value of for which lies between the roots of , is
none of these
The correct Answer is:3
Minimun value of is at x =0.
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - MATRIX MATCH TYPE
6 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - NUMERICAL VALUE TYPE
43 Videos
- THEORY OF EQUATIONSBOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - Multiple Correct Answer Type
38 Videos
- STRAIGHT LINESBOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - ARCHIVES (NUMERICAL VALUE TYPE)
1 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
294 Videos
Similar Questions
In the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.
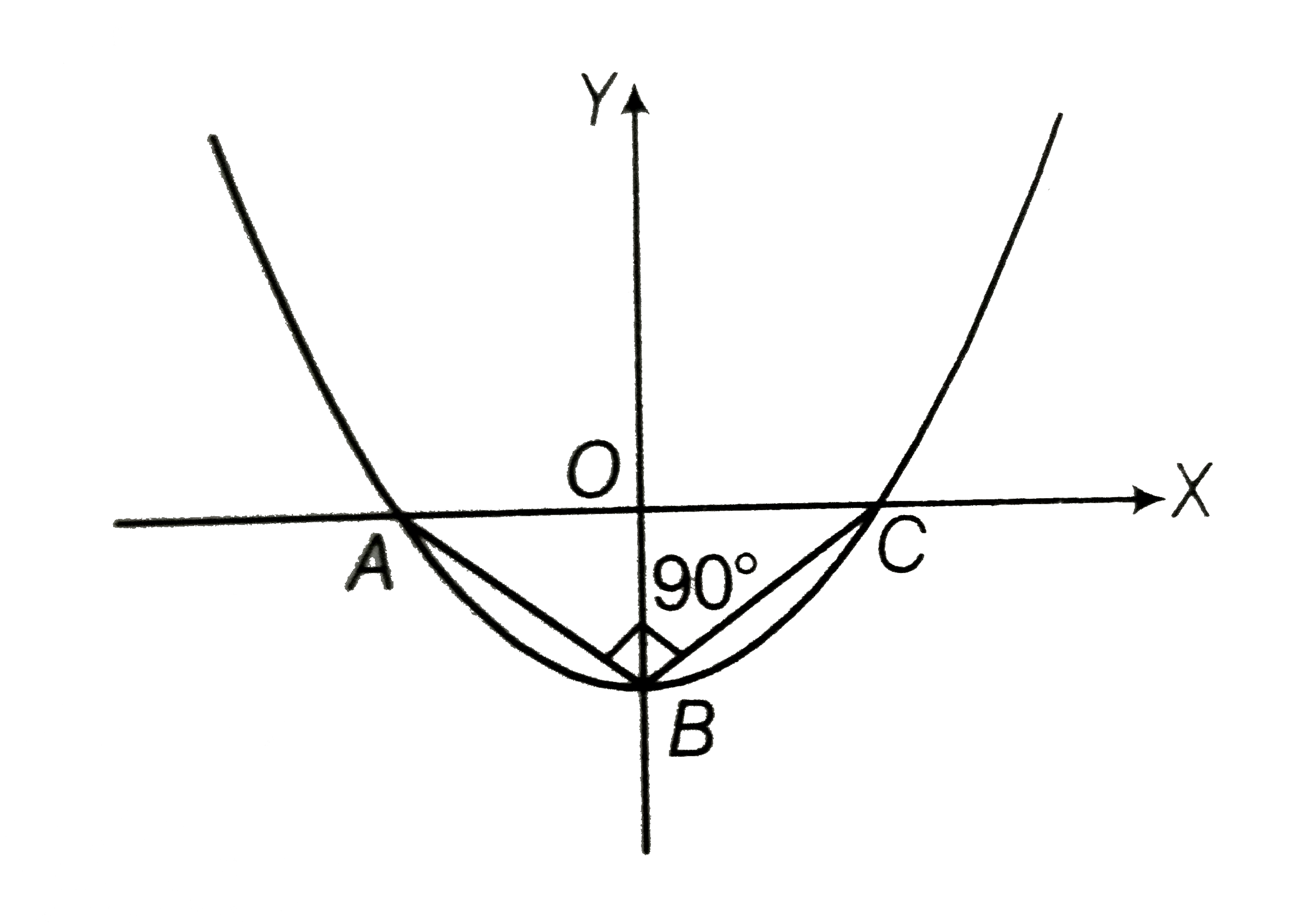
y=f(x) is given by
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔABC is right angled isosceles triangle whose hypotenuse AC=4√2 units.
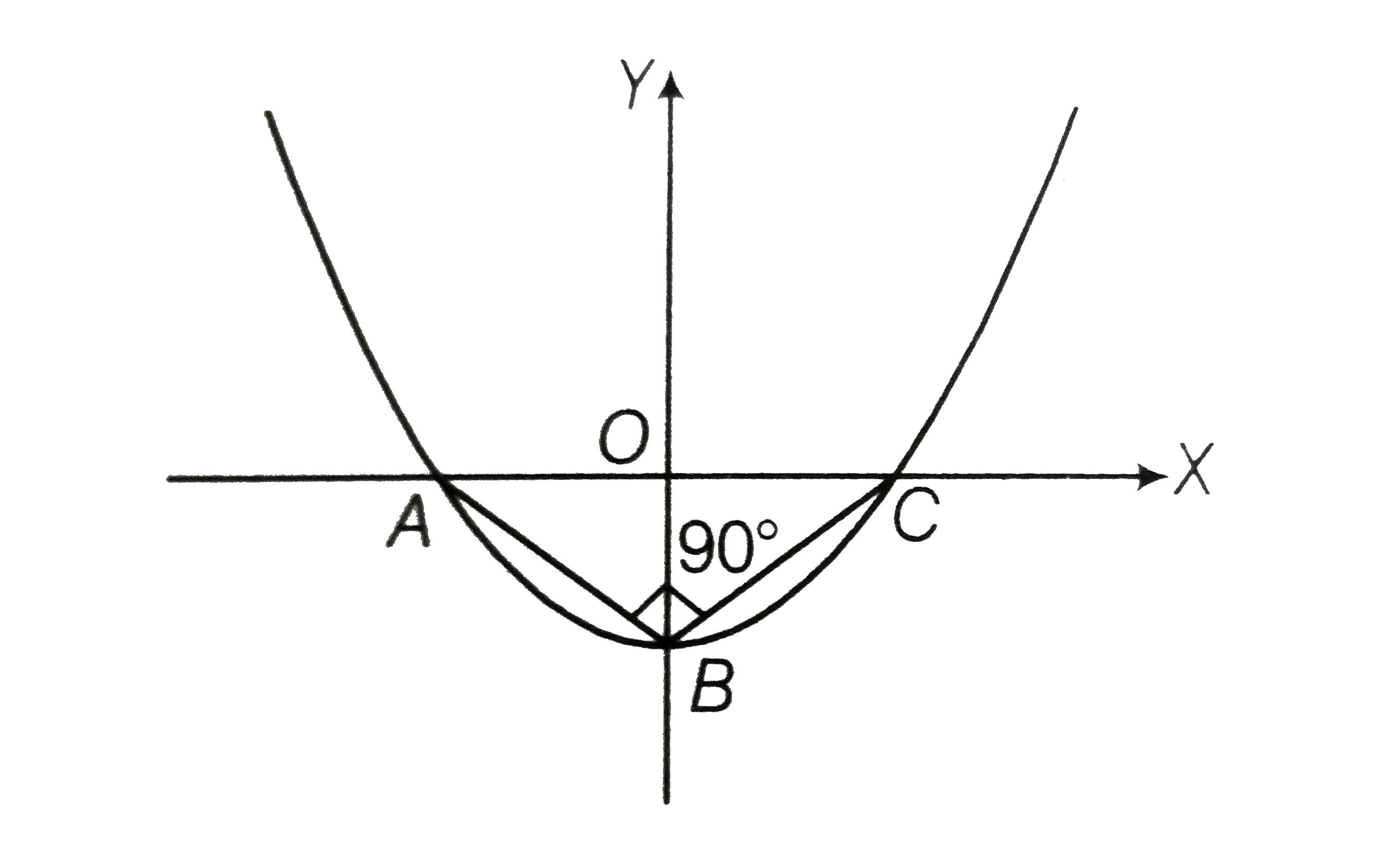
Minimum valueof y=f(x) is
View Solution
Knowledge Check
ΔABC is a right angled isosceles triangle and ∠B is the right angle in the triangle. If AC measures 7√2, then which one of the lengths of AB and BC, respectively?
A7,7B9,9C10,10D11,12
Value of λ so that point (λ,λ2) lies between the lines |x+2y|=3 is
View SolutionLet f(x)=ax2+bx+c, a≠0, a, b, c∈I. Suppose that f(1)=0, 50<f(7)<60 and 70<f(8)<80.
Number of integral values of x for which f(x)<0 is
View SolutionA right angled isosceles triangle is inscribed in the circle x2+y2_4x−2y−4=0 then length of its side is
View SolutionA right angled isosceles triangle is inscribed in the circle x2+y2−4x−2y−4=0 then length of the side of the triangle is
View SolutionFind the equations of the sides of an isosceles right angled triangle the equation of whose hypotenuse is 3x+4y=4 and the opposite vertex is the point (2, 2).
View SolutionFind the equation of one of the side of an isosecles right angled triangle whose hypotenuse is given by 3x + 4y = 4 and the opposite vertex of the hypotenuse is (2,2).
View SolutionThree balls each of mass 0.5 kg are kept at the vertices of an isosceles right triangle with its hypotenuse of 2√2 m. What will be the net gravitational force on the ball kept at the vertex of right angle ?
View Solution
