Value of λ so that point (λ,λ2) lies between the lines |x+2y|=3 is
(−12,2)
(−32,2)
(−32,1)
(−1,32)
The correct Answer is:C
To find the value of λ such that the point (λ,λ2) lies between the lines defined by the equation |x+2y|=3, we can follow these steps:
Step 1: Understand the Lines
The equation |x+2y|=3 represents two lines:
1. \( x + 2y = 3 \)
2. \( x + 2y = -3 \)
Step 2: Substitute the Point
We need to check if the point \( (lambda, lambda^2) \) lies between these two lines. We substitute \( x = lambda \) and \( y = lambda^2 \) into the equations of the lines.
Step 3: Set Up the Inequality
For the point to lie between the two lines, the following condition must hold:
\(
(x + 2y - 3)(x + 2y + 3) < 0
\)
Substituting \( x = lambda \) and \( y = lambda^2 \):
\(
(lambda + 2(lambda^2) - 3)(lambda + 2(lambda^2) + 3) < 0
\)
Step 4: Simplify the Expressions
Calculating the expressions:
1. First expression: \( lambda + 2lambda^2 - 3 \)
2. Second expression: \( lambda + 2lambda^2 + 3 \)
Now we can rewrite the inequality:
\(
(2lambda^2 + lambda - 3)(2lambda^2 + lambda + 3) < 0
\)
Step 5: Analyze the Quadratic
Let \( f(lambda) = 2lambda^2 + lambda - 3 \) and \( g(lambda) = 2lambda^2 + lambda + 3 \).
1. For \( g(lambda) \): Since the leading coefficient (2) is positive and the constant term is positive, \( g(lambda) > 0 \) for all \( lambda \).
2. For \( f(lambda) \): We need to find the roots of \( f(lambda) = 0 \) using the quadratic formula:
\(
lambda = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-1 \pm \sqrt{1^2 - 4(2)(-3)}}{2(2)}
\)
\(
= \frac{-1 \pm \sqrt{1 + 24}}{4} = \frac{-1 \pm 5}{4}
\)
This gives us the roots:
\(
lambda_1 = 1 \quad \text{and} \quad lambda_2 = -\frac{3}{2}
\)
Step 6: Determine the Intervals
The quadratic \( f(lambda) \) opens upwards (since the coefficient of \( lambda^2 \) is positive). The roots divide the number line into intervals:
1. \( (-\infty, -\frac{3}{2}) \)
2. \( (-\frac{3}{2}, 1) \)
3. \( (1, \infty) \)
Since \( f(lambda) < 0 \) between the roots, the solution to the inequality is:
\(
-\frac{3}{2} < lambda < 1
\)
Final Answer
The value of \( lambda \) such that the point \( (lambda, lambda^2) \) lies between the lines \( |x + 2y| = 3 \) is:
\(
\boxed{(-\frac{3}{2}, 1)}
\)
The equation |x+2y|=3 represents two lines:
1. \( x + 2y = 3 \)
2. \( x + 2y = -3 \)
We need to check if the point \( (lambda, lambda^2) \) lies between these two lines. We substitute \( x = lambda \) and \( y = lambda^2 \) into the equations of the lines.
For the point to lie between the two lines, the following condition must hold:
\(
(x + 2y - 3)(x + 2y + 3) < 0
\)
Substituting \( x = lambda \) and \( y = lambda^2 \):
\(
(lambda + 2(lambda^2) - 3)(lambda + 2(lambda^2) + 3) < 0
\)
Calculating the expressions:
1. First expression: \( lambda + 2lambda^2 - 3 \)
2. Second expression: \( lambda + 2lambda^2 + 3 \)
\(
(2lambda^2 + lambda - 3)(2lambda^2 + lambda + 3) < 0
\)
Let \( f(lambda) = 2lambda^2 + lambda - 3 \) and \( g(lambda) = 2lambda^2 + lambda + 3 \).
2. For \( f(lambda) \): We need to find the roots of \( f(lambda) = 0 \) using the quadratic formula:
\(
lambda = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} = \frac{-1 \pm \sqrt{1^2 - 4(2)(-3)}}{2(2)}
\)
\(
= \frac{-1 \pm \sqrt{1 + 24}}{4} = \frac{-1 \pm 5}{4}
\)
This gives us the roots:
\(
lambda_1 = 1 \quad \text{and} \quad lambda_2 = -\frac{3}{2}
\)
The quadratic \( f(lambda) \) opens upwards (since the coefficient of \( lambda^2 \) is positive). The roots divide the number line into intervals:
1. \( (-\infty, -\frac{3}{2}) \)
2. \( (-\frac{3}{2}, 1) \)
3. \( (1, \infty) \)
\(
-\frac{3}{2} < lambda < 1
\)
The value of \( lambda \) such that the point \( (lambda, lambda^2) \) lies between the lines \( |x + 2y| = 3 \) is:
\(
\boxed{(-\frac{3}{2}, 1)}
\)
Topper's Solved these Questions
Similar Questions
The point (α2+2λ+5,λ2+1) lies on the line x+y=10 for:
View SolutionIn the given figue vertices of ΔABC lie on y=f(x)=ax2+bx+c. The ΔAB is right angled isosceles triangle whose hypotenuse AC=4√2 units.
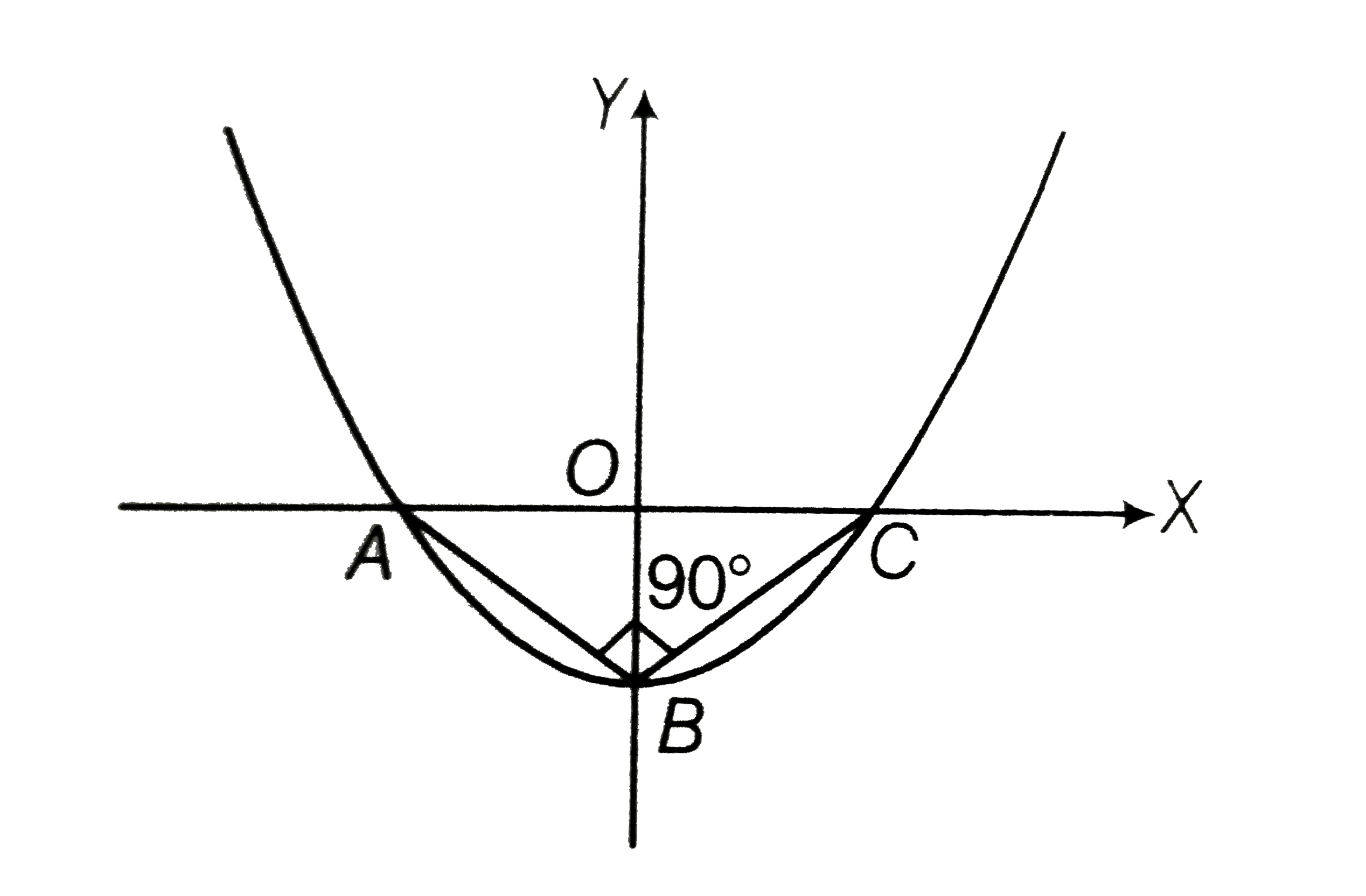
Number of integral value of λ for which λ2 lies between the roots of f(x)=0, is
View SolutionThe sum of all intergral values of λ for which (λ2+λ−2)x2+(λ+2)x<1∀x∈R, is:
View SolutionThe value of λ or which the straighat line x−λ3=y−12+λ=z−3−1 may lie on the plane x−2y=0 (A) 2 (B) 0 (C) −12 (D) there is no such λ
View SolutionThe values of λ for which the line y=x+λ touches the ellipse 9x2+16y2=144 , are
View SolutionFind values of lamda for which 1log3λ+1log4λ>2 .
View SolutionSum of the possible values of λ for which the following threes line
x+y=1,λx+2y=3,λ2x+4y+9=0 are concurrent is
View SolutionFind the value of |a| for which the area of triangle included between the coordinate axes and any tangent to the curve xya=λa+1 is constant (where λ is constant.)
View SolutionFind the value of |a| for which the area of triangle included between the coordinate axes and any tangent to the curve xay=λa is constant (where λ is constnat.),
View SolutionTwo parabolas y2=4a(x−λ1)andx2=4a(y−λ2) always touch each other (λ1,λ2 being variable parameters). Then their point of contact lies on a
View Solution

